 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Операции над массивами ⇐ ПредыдущаяСтр 4 из 4
Формирование массива, как было показано выше, осуществляется прямым (построчным) перечислением его элементов подобно А=[1 3 5 7; 4 5 6 7] (2 строки и 4 столбца), В=[1; 3; 5; 7] (столбец с 4 элементами) или заданием диапазона значений с заданным (или умалчиваемым единичным) шагом [1:2:7], [4:7], [ [1:2:7]; [4:7] ] и т.п. Доступ к элементам или блокам элементов массива производится указанием индексов или массива индексов: A(2,k) - элемент второй строки и k-го столбца; A(:,k) - k-й столбец; A(1:3; 1:4) - подматрица из первых 3 строк и 4 столбцов матрицы; C(:, :, 12) -12-я страница трехмерного массива. Следует учесть, что хранение массивов в памяти ведется по столбцам. Поэтому возможна работа с созданным многомерным массивом как с одномерным, например, A(:) - вектор-столбец из всех элементов массива А, A(13:17) - столбец из элементов с номерами от 13 до 17. Имеется возможность объединять массивы "по горизонтали"- [A, B, C] или [A B C] (массивы с одинаковым числом строк) и"по вертикали"-[A; B;C] (массивы с одинаковым числом столбцов). Из вектора можно удалить одинаковые элементы функцией unique(X). Существует возможность объединения множеств - union(X,Y), пересечения - intersect(X,Y), разности - setdiff(X,Y):
Функция find дает поиск по условию элементов одно- или двухмерного массива в формате команд k=find(X<условие>), [i,j]=find(A<условие>) (если условия нет, отыскиваются ненулевые элементы):
Для определение длины вектора используется функция length :
и для размеров массива - функцию size :
Суммирование и умножение элементов массива можно реализовать функциями sum(A) и prod(A) (для двумерного массива выполняется поиск сумм и произведений по столбцам). С помощью функций sum(A,dim) и prod(A,dim) можно выполнить операции по измерению dim. Функцию sum часто используют для поиска скалярного произведения векторов
Сортировку элементов массива по возрастанию можно выполнить функцией sort(A,dim) , причем команда [B,I]= sort(A) выдает и список индексов. Сортировку по убыванию можно выполнить аналогичной функциейsortrows. Среди других следует отметить и ряд функций комбинаторики: perms(V) -перестановки всех элементов вектора V размерности n (массив размерности n! x n) : >> perms (3:2:7) ans =[ 7 5 3; 5 7 3; 7 3 5; 3 7 5; 5 3 7; 3 5 7] >> perms([3 2 7]) ans =[ 7 2 3; 2 7 3; 7 3 2; 3 7 2; 2 3 7; 3 2 7] ; nchoosek(n,k) - число сочетаний из n по k =n!/ (k! (n-k)!): >> nchoosek(7,2) ans = 21; nchoosek(V,k) - массив всех сочетаний элементов вектора V: >> nchoosek([3 2 7],2) ans = [ 3 2; 3 7; 2 7 ]; Иногда могут быть полезными функции начального задания: zeros(n), zeros(m,n), zeros(size(А)) - формирование массива нулей (одномерного, двумерного, соразмерного с массивом А); допус-тимо формирование массива и большей размерности zeros(m,n,p,...) ; ones(n), ones (m,n), ones (size(А)) - формирование массива единиц ; rand(n), rand (m,n), rand (size(А)) - формирование массива чисел с равномерным законом распределения в (0,1); randn(n), randn (m,n), randn (size(А)) -формирование массива чисел с нормальным законом распределения (Mx=0, Dx=1); eye(n), eye(m,n), eye(size(A)) - формирование единичной матрицы (n x n, m x n, соразмерной с матрицей А):
Отметим также и некоторые полезные конструкции: cross(X,Y) - векторное произведение(X,Y-трехмерные векторы): X x Y= [ (X2Y3-X3Y2), (X3Y1-X1Y3), (X1Y2-X2Y1)] ; kron(X,Y) - тензорное произведение (произведение Кронекера):
|Xm1Y Xm2Y ... XmnY | meshgrid(X,Y), meshgrid(X,Y,Z) -формирование двумерной (трехмерной) сетки (обычно используется при реализации графики): [x,y]=meshgrid(-2:0.1:2, -10:0.5:10) Ряд других функций, связанных с обработкой массивов, рассмотрен ниже.
Поиск по сайту: |
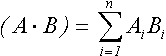 в форме sum(A.*B):
в форме sum(A.*B):