|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Элементарные математические функции
Из многообразия т.н. элементарных встроенных математических функций отметим лишь некоторые наиболее известные или оригинальные. Аргументами большинства из приведенных ниже функций являются не только скаляры, но и массивы. pi = 4*atan(1)=imag(log(-1))=3.1415926535897..; abs(X)- абсолютная величина: для комплексного числа a+bi его модуль равен angle(X) - аргумент комплексного числа (из диапазона [-p,p ]): комплексное X=a+bi представимо как r·eij, где a = r cosj, b = r sin j:
real(X), imag(X) - действительная и мнимая часть числа; conj(X) - комплексно-сопряженное:
ceil(X), fix(X), floor(X), round(X) - округления (до ближайшего целого, не меньшего Х; отбрасывание дробной части; до ближайшего целого, не большего Х; до ближайшего целого); mod(X,Y) - остаток от деления X на Y; sign(X) - знак числа (для комплексных X / |X|); gcd(m,n) -наибольший общий делитель для целых чисел; если использовать оператор [g,c,d]=gcd(m,n), то дает указанный делитель и множители c,d такие , что g==m*c+n*d :
lcm(m,n) - наименьшее общее кратное:
rat(X) , rat (X,k) - представление цепной дробью с точностью |X|·10-k/2 (по умолчанию |X|·10-6 ):
rats(X), rats(X,k)- представление отношением целых чисел :
sqrt(X) - квадратный корень :
exp(X) - экспонента ex (ex+iy= ex(cos y+i siny)) :
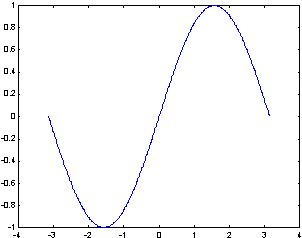
pow2(X) - двоичная экспонента 2x; log(X) - натуральный логарифм; log2(X), log10(X) -логарифм по основанию 2 и основанию 10; sin(X) cos(X) tan(X) cot(X) csc(X) sec(X) - тригонометрические функции (синус, косинус, тангенс, котангенс, косеканс, секанс): sin(x+iy)=sin(x) ch(y) +i cos(x) sh(y); cos(x+iy)=cos(x) ch(y) -i sin(x) sh(y),
asin(X) acos(X) atan(X) acot(X) acsc(X) asec(X) - обратные тригонометрические функции (арксинус, арккосинус и т.д.):
atan2(Y,X)- круговой арктангенс Arctg (только для действительных частей аргументов), берется в интервале [-p,p ]; sinh(X) cosh(X) tanh(X) coth(X) csch(X) sech(X) - гиперболические функции (синус, косинус, тангенс, котангенс, косеканс, секанс): sh(X)=(eX-e-X)/2 , ch(X)=(eX+e-X)/2 и др.; asinh(X) acosh(X) atanh(X) acoth(X) acsch(X) asech(X) - обратные гиперболические функции:
erf (Х)- интеграл вероятностей (функция Гаусса, функция ошибок)
и родственные функции : erfc(х)=1-erf(x) (дополнительный интеграл вероятностей) ; erfcx(х)=exp(x2)·erfc(x) (нормированный дополнительный интеграл вероятностей); erfinv(х) (аргумент, для которого интеграл вероятностей равен х); gamma(х) -гамма-функция
и родственные функции : gammainc(x,a)= gammaln(x)=ln Г(х) (логарифмическая гамма-функция); beta(x,y) - бета-функция функции преобразования координат: специальные функции(цилиндрические функции Бесселя, Неймана, Ханкеля; функции Эйри, эллиптические функции Якоби и эллиптические интегралы, интегральная показательная функция, присоединенные функции Лежандра и много других функций, полезных при изучении физических процессов), функции линейной алгебры, аппроксимации данных, численного интегрирования, поиска корней уравнений, обслуживания графики, обработки дат, множестви др. Если вы имеете намерение познакомиться с поведением какой-то из функций, поступите по аналогии с примитивным примером:
Поиск по сайту: |
 / abs(3-4i)=5 , abs(-13)=13;
/ abs(3-4i)=5 , abs(-13)=13; ,
, 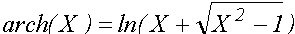
 ,
,  ,
, 
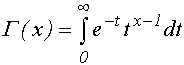 (при целочисленных х Г(1+х)=х!)
(при целочисленных х Г(1+х)=х!) (неполная гамма-функция);
(неполная гамма-функция);