|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Элементарные операционные узлы ЭВМ. Триггеры
Операционный узел состоит из устройств, в которых обрабатывается и хранится информация, а именно: счетчиков, регистров, дешифраторов, сумматоров, схем сравнения, блоков памяти и т. п. Используя набор этих устройств, можно производить обработку поступающей информации. Результатом ее обработки является выходная информация. Триггер — устройство, которое может находиться в одном из двух устойчивых состояний и сохранять его теоретически бесконечно долго. Любой триггер является схемой с памятью или автоматом. Переключение триггера происходит по входному сигналу извне. По способу синхронизации различают синхронные и асинхронные триггерные схемы. По структурному построению — однотактные (триггеры защелки), двухтактные и триггеры с динамических управлением. По способу реакции на помехи — прозрачные и непрозрачные. Непрозрачные, в свою очередь, делятся на проницаемые и непроницаемые. По функциональному назначению — RS, D, JK, T, RR, SS, EE, DV. При изготовлении триггеров применяются преимущественно полупроводниковые приборы (транзисторы), реже — электронные лампы. Используются в основном в вычислительной технике для организации компонентов вычислительных систем: регистров, счётчиков, ОЗУ. Насчитывается несколько видов триггеров: D-триггеры, JK-триггеры, RS-триггеры, T-триггеры. Из названий триггеров можно определить количество входов. Так у D-триггера есть всего один вход D, а у JK — два входа J и K. Если триггер является синхронным — добавляется вход синхронизации C. Каждый тип триггера имеет таблицу работы (таблицу истинности), в которой указывается как различные значения на входах триггера влияют на его состояние. Состояние триггера обозначают буквой Q. Индекс возле буквы означает состояние до подачи сигнала (t) или после подачи сигнала (t+1). Рассмотрим эти таблицы для перечисленных триггеров в асинхронном режиме (без входа С).
Если триггер синхронный, то существует также дополнительный вход синхронизации. При записи информации в триггер на него необходимо подать 1. Шифраторы Операционный узел состоит из устройств, в которых обрабатывается и хранится информация, а именно: счетчиков, регистров, шифраторов, дешифраторов, сумматоров, схем сравнения, блоков памяти и т. п. Используя набор этих устройств, можно производить обработку поступающей информации. Результатом ее обработки является выходная информация. Шифратор - это логическая схема с N входами и М выходами (М<="" p=""> Назначение шифратора - выдавать на выходе информацию о том, на какой из входов подан сигнал, используя при этом кодовое слово, содержащее минимум двоичных разрядов, требующееся для этого задания. Один из простейших примеров шифратора является шифратор, имеющий четыре входа и два выхода. Этот пример мы и рассмотрим. Составим таблицу, в которой каждому входному сигналу сопоставим последовательность из двух выходных сигналов.
На основании данной таблицы истинности составим формулу для функций X и Y:
На основании полученных функций построим логическую схему. Схема должна иметь четыре входа для переменных А, В, C, D и два выхода для функций X, Y. Схема должна иметь четыре входа и два выхода.
Дешифратор Операционный узел состоит из устройств, в которых обрабатывается и хранится информация, а именно: счетчиков, регистров, шифраторов, дешифраторов, сумматоров, схем сравнения, блоков памяти и т. п. Используя набор этих устройств, можно производить обработку поступающей информации. Результатом ее обработки является выходная информация. Дешифратор - преобразователь кодов, выполняющий преобразование входных двоичных кодов в выходной унитарный код. Унитарный код двоичного n – разрядного числа представляется 2n разрядами, только один из разрядов которого равен 1 (или 0). Условное описание дешифратора задаётся формулой nxm (n на m), для полного дешифратора это формула nx2n. Примерами полных являются дешифраторы: 1x2, 2x4, 3x8, 4x16. Рассмотрим пример. Составим таблицу, в которой каждому выходному сигналу сопоставляется последовательность из двух входных сигналов.
На основании данной таблицы истинности составим формулу для функций A, B, C и D:
На основании полученных функций построим логическую схему. Схема должна иметь два входа и четыре выхода.
Мультиплексор Операционный узел состоит из устройств, в которых обрабатывается и хранится информация, а именно: счетчиков, регистров, шифраторов, дешифраторов, сумматоров, схем сравнения, блоков памяти и т. п. Используя набор этих устройств, можно производить обработку поступающей информации. Результатом ее обработки является выходная информация. Мультиплексором называется комбинационная схема, имеющая m+2m входов и один выход, где m – количество адресных входов, а 2m – количество информационных входов мультиплексора. Адреса представляются в двоичном коде и им присваивается номер j. Каждому адресу с номером j соответствует свой информационный вход Aj , сигнал с которого при данном адресе проходит на выход. Основным назначением мультиплексора является коммутация 2m входных сигналов на один выход. Таким образом, мультиплексор выполняет функцию
где X – двоичный код адреса; Aj – входные информационные сигналы мультиплексора; Kj(X) – конституенты 1, принимающие значения, равные 1 на единственном наборе переменных X = j. Условное описание мультиплексора задаётся формулой 2mx1. Примерами являются мультиплексоры: 2x1, 4x1, 8x1, 16x1. В состав мультиплексора обычно включают двоичный дешифратор, как показано на рисунке 10.1. Это позволяет управлять переключением информационных входов при помощи двоичных кодов, подаваемых на управляющие входы. Количество информационных входов в таких схемах выбирают кратным степени числа два.
Условно графическое обозначение четырёхвходового мультиплексора с двоичным управлением приведено на рисунке 10.2. Входы A0 и A1 являются управляющими входами мультиплексора, определяющими адрес входного сигнала, который будет соединён с выходным выводом мультиплексора Y. Сами входные сигналы обозначены как X0, X1, X2 и X3.
Демультиплексор Операционный узел состоит из устройств, в которых обрабатывается и хранится информация, а именно: счетчиков, регистров, шифраторов, дешифраторов, сумматоров, схем сравнения, блоков памяти и т. п. Используя набор этих устройств, можно производить обработку поступающей информации. Результатом ее обработки является выходная информация. Демультиплексорами называются устройства, которые позволяют подключать один вход к нескольким выходам. Демультиплексор можно построить на основе точно таких же схем логического "И", как и при построении мультиплексора. Существенным отличием от мультиплексора является возможность объединения нескольких входов в один без дополнительных схем. Однако для увеличения нагрузочной способности микросхемы, на входе демультиплексора для усиления входного сигнала лучше поставить инвертор. Схема демультиплексора приведена на рисунке 1.1. В этой схеме для выбора конкретного выхода демультиплексора, как и в мультиплексоре, используется двоичный дешифратор.
Однако, если рассмотреть принципиальную схему самого дешифратора, то можно значительно упростить демультиплексор. Достаточно просто к каждому логическому элементу 'И', входящему в состав дешифратора просто добавить ещё один вход – In. Такую схему часто называют дешифратором с входом разрешения работы. Условно-графическое изображение демультиплексора приведено на рисунке 11.2.
В этом обозначении вход In обозначен как вход E, а выходы не названы никак, оставлены только их номера. Регистр Операционный узел состоит из устройств, в которых обрабатывается и хранится информация, а именно: счетчиков, регистров, шифраторов, дешифраторов, сумматоров, схем сравнения, блоков памяти и т. п. Используя набор этих устройств, можно производить обработку поступающей информации. Результатом ее обработки является выходная информация. Регистром называется схема, служащая для запоминания многоразрядных двоичных слов (кодов) и состоящая из необходимого количества триггеров. Различают:
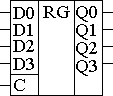
Параллельный регистр служит для запоминания многоразрядного двоичного (или недвоичного) слова. Количество триггеров, входящее в состав параллельного регистра определяет его разрядность. Схема четырёхразрядного параллельного регистра приведена на рисунке 12.1, а его условно-графическое обозначение - на рисунке 12.2.
В условно-графическом обозначении возле каждого входа D указывается степень двоичного разряда, который должен быть запомнен в этом триггере регистра. Точно таким же образом обозначаются и выходы регистра. То, что микросхема является регистром, указывается в центральном поле условно-графического обозначения символами RG. В приведённом на рисунке 12.2 условно-графическом обозначении параллельного регистра инверсные выходы триггеров не показаны. В микросхемах регистров инверсные выходы триггеров часто не выводятся наружу для экономии количества выводов корпуса.
При записи информации в параллельный регистр все биты (двоичные разряды) должны быть записаны одновременно. Поэтому все тактовые входы триггеров, входящих в состав регистра, объединяются параллельно. Для уменьшения входного тока вывода синхронизации C на этом входе в качестве усилителя часто ставится инвертор. Следует помнить, что назначение разрядов является условным. Если по каким либо причинам (например, с точки зрения разводки печатной платы) удобно изменить нумерацию разрядов, то это можно свободно сделать. При перенумерации входов регистров нужно не забывать, точно таким же образом, изменить номера выходов параллельного регистра. Для реализации параллельного регистра можно использовать как триггеры с статическим, так и с динамическим входом синхронизации. В переводной литературе при использовании для построения параллельного регистра триггеров-защелок этот регистр, в свою очередь, называют регистром-защелкой. При использовании регистров со статическим входом тактирования следует соблюдать осторожность, так как при единичном потенциале на входе синхронизации C. сигналы с входов регистра будут свободно проходить на его выходы. В таких случаях обычно используется двухтактная синхронизация, подобная рассмотренной в главе, посвященной использованию одновибраторов.
Последовательные регистры Кроме параллельного соединения триггеров для построения регистров используются последовательное соединение этих элементов. Последовательный регистр (регистр сдвига) обычно служит для преобразования последовательного кода в параллельный и наоборот. Применение последовательного кода связано с необходимостью передачи большого количества двоичной информации по ограниченному количеству соединительных линий. При параллельной передаче разрядов требуется большое количество соединительных проводников. Если двоичные разряды последовательно бит за битом передавать по одному проводнику, то можно значительно сократить размеры соединительных линий на плате (и размеры корпусов микросхем). Принципиальная схема последовательного регистра, собранного на основе D?триггеров и позволяющего осуществить преобразование последовательного кода в параллельный, приведена на рисунке 12.3.
В этом регистре триггеры соединены последовательно, то есть выход первого соединён с входом второго и т.д. Условно-графическое изображение рассмотренного последовательного регистра приведено на рисунке 12.4.
Входы синхронизации в последовательных регистрах, как и в параллельных, объединяются. Это обеспечивает одновременность смены состояния всех триггеров, входящих в состав последовательного регистра. Преобразование последовательного кода в параллельный производится следующим образом. Отдельные биты двоичной информации последовательно подаются на вход D0. Каждый бит сопровождается отдельным тактовым импульсом, который поступает на вход синхронизации C. После поступления первого тактового импульса логический уровень, присутствующий на входе D0, запоминается в первом триггере и поступает на его выход, а так как он соединён с входом второго триггера, то и на его вход. После поступления второго тактового импульса логический уровень, присутствующий на входе второго триггера, запоминается в нем и поступает на его выход, а так как он соединён с входом третьего триггера, то и на его вход. Одновременно следующий бит запоминается в первом триггере. После поступления четвертого тактового импульса в триггерах регистра будут записаны уровни бит, которые последовательно присутствовали на входе D0. Теперь этими битами можно воспользоваться, например, для отображения на индикаторах. Пусть на вход регистра поступает сигнал, временная диаграмма которого изображена на рисунке 12.5, тогда состояние выходов этого регистра будет последовательно принимать значения, записанные в таблице 12.1.
На рисунке 12.5 вместе с логическими уровнями записываются значения бит, которые передаются по соединительной линии или присутствуют на выходах сдвигового регистра.
Универсальные регистры Регистры сдвига выполняют обычно как универсальные последовательно-параллельные микросхемы. Это связано с необходимостью записи в регистр параллельного двоичного кода при преобразовании параллельного кода в последовательный. Переключение регистра из параллельного режима работы в последовательный и наоборот осуществляется при помощи мультиплексора (коммутатора). Использование коммутатора позволяет входы триггеров регистра либо подключать к внешним выводам микросхемы, либо подключать к выходу предыдущего триггера. Счетчик Операционный узел состоит из устройств, в которых обрабатывается и хранится информация, а именно: счетчиков, регистров, шифраторов, дешифраторов, сумматоров, схем сравнения, блоков памяти и т. п. Используя набор этих устройств, можно производить обработку поступающей информации. Результатом ее обработки является выходная информация. Счётчиком называется цифровой автомат, служащий для формирования многоразрядных двоичных слов (кодов) соответствующих количеству входных импульсов. По мере поступления входных импульсов счётчик последовательно перебирает свои состояния в определённом для данной схемы порядке. Длина списка используемых состояний называется модулем пересчёта М, основанием пересчёта или ёмкостью счётчика. Одно из возможных состояний счётчика принимается как начальное или нулевое. Если счётчик начал считать с начального состояния и через каждые М входных сигналов в нём снова устанавливается начальное состояние, а на выходе счётчика формируется сигнал М–ичного переноса P, то такой счётчик называется счётчиком–делителем частоты. Частота следования М-ичного переноса P в таком счётчике меньше частоты входных импульсов ровно в M раз. Различные схемы счётчиков могут перебирать свои состояния в самом различном порядке. Порядок перебора кодов состояний счётчика определяется системой кодирования состояний счётчика как цифрового автомата. Чаще всего применяются двоичные счётчики, у которых порядок смены состояний триггеров соответствует последовательности двоичных чисел. Счетчик может перебирать свои состояния в возрастающем порядке чисел и тогда он называется суммирующим. Если счётчик перебирает свои состояния в порядке убывания двоичных чисел, то он называется вычитающим. Если под действием сигналов управления порядок перебора может изменяться на противоположный, то счётчик называется реверсивным. Счётчики строятся с использованием синхронизированных триггеров. Если несколько триггеров блока памяти имеют общий синхросигнал, то они образуют синхронный счётчик. Несколько синхронных счётчиков соединённых по схеме подачи синхросигналов последовательно образуют асинхронный счётчик. В этом случае сигнал выходного переноса предыдущего счётчика используется как сигнал синхронизации последующего счётчика.
Асинхронные счетчики. Простейший вид счётчика - двоичный может быть построен на основе T-триггера. T-триггер изменяет своё состояние на прямо противоположное при поступлении на его вход синхронизации импульсов. Для реализации T-триггера воспользуемся универсальным D-триггером с обратной связью, как это показано на рисунке 13.1.
Так как эта схема, как мы уже рассматривали ранее, при поступлении на вход импульсов меняет свое состояние на противоположное, то её можно рассматривать как счётчик, считающий до двух. Временные диаграммы сигналов на входе и выходах T-триггера приведены на рисунке 13.2.
Обычно требуется посчитать большее количество импульсов. В этом случае можно использовать выходной сигнал первого счетного триггера как входной сигнал для следующего триггера, то есть соединить триггеры последовательно. Так можно построить любой счётчик, считающий до максимального числа, кратного степени два. Схема счётчика, позволяющего посчитать любое количество импульсов, меньшее шестнадцати, приведена на рисунке 13.3. Количество поступивших на вход импульсов можно узнать, подключившись к выходам счётчика Q0 … Q3. Это число будет представлено в двоичном коде.
Синхронные счётчики. В рассмотренных схемах делителей частоты быстродействие всей схемы определяется временем распространения сигнала от входа до выхода самого старшего разряда. При этом получается, что чем больше требуемый коэффициент деления, тем больше двоичных разрядов счётчика требуется для реализации этого делителя. Тем большее время требуется для распространения сигнала от входа синхронизации счётчика, до его выхода, и тем меньше будет предельная частота, которую можно подавать на вход этого делителя. Первая схема, которую мы рассмотрим - это схема кольцевого счётчика. Такой счётчик можно построить на основе сдвигового регистра. Схема кольцевого счётчика приведена на рисунке 13.4.
Рассмотрим работу этой схемы. Пусть первоначально в счетчике записано число 002. После первого же тактового импульса состояние счётчика станет равным 102, после второго - 112. Временные диаграммы этой схемы приведены на рисунке 13.5.
В результате анализа временных диаграмм можно определить, что коэффициент деления схемы кольцевого счётчика будет равен: Кд = 2*n. Для того чтобы избежать неправильной работы счётчика в этот счётчик можно ввести схему контроля правильной работы. В простейшем случае это может быть обычный логический элемент “И-НЕ”. Этот элемент будет контролировать состояние счётчика, соответствующее единицам во всех его разрядах. Схема 2-разрядного счётчика со схемой проверки правильности его работы приведена на рисунке 13.6.
В этой схеме триггеры счётчика при поступлении импульсов на тактовый вход последовательно заполняются единицами. Как только все триггеры будут заполнены единицами, на выходе логического элемента “2И-НЕ” появится уровень логического нуля. При поступлении следующего тактового импульса этот ноль будет записан в первый триггер счётчика. В дальнейшем работа счётчика повторяется. Временные диаграммы сигналов на выходах этого счётчика приведены на рисунке 13.7.
Сумматор Операционный узел состоит из устройств, в которых обрабатывается и хранится информация, а именно: счетчиков, регистров, шифраторов, дешифраторов, сумматоров, схем сравнения, блоков памяти и т. п. Используя набор этих устройств, можно производить обработку поступающей информации. Результатом ее обработки является выходная информация. Сумматор - логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. При арифметическом сложении выполняются и другие дополнительные операции: учет знаков чисел, выравнивание порядков слагаемых и тому подобное.
Сумматоры классифицируются по разным признакам: 1. В зависимости от системы исчисления:
2. По количеству одновременно обрабатываемых разрядов складываемых чисел:
3. По числу входов и выходов одноразрядных двоичных сумматоров:
4. По способу представления и обработки складываемых чисел многоразрядные сумматоры подразделяются на:
Построение двоичных сумматоров обычно начинается с сумматора по модулю 2. На рисунке 14.1 приведена таблица истинности этого сумматора. Ее можно получить исходя из правил суммирования в двоичной арифметике.
Схема сумматора по модулю 2 приведена на рисунке 14.2.
Сумматор по модулю 2 (для двоичной арифметики его схема совпадает со схемой исключающего "ИЛИ") изображается на схемах как показано на рисунке 14.3.
Сумматор по модулю 2 выполняет суммирование без учета переноса. В полном двоичном сумматоре требуется учитывать перенос, поэтому требуются схемы, позволяющие формировать перенос в следующий двоичный разряд. Таблица истинности такой схемы, называемой полусумматором, приведена на рисунке 14.4.
Принципиальная схема, реализующая таблицу истинности полусумматора представлена на рисунке 14.5. Полусумматор изображается на схемах как показано на рисунке 14.6.
Схема полусумматора формирует перенос в следующий разряд, но не может учитывать перенос из предыдущего разряда, поэтому она и называется полусумматором. Таблицу истинности полного двоичного одноразрядного сумматора можно получить из правил суммирования двоичных чисел. Она приведена на рисунке 14.7. В обозначении входов использовано следующее правило: в качестве входов использованы одноразрядные числа A и B; перенос обозначен буквой P; для обозначения входа переноса используется буква I (сокращение от английского слова input – вход); для обозначения выхода переноса используется буква O (сокращение от английского слова output – выход).
По таблице 14.7 составим схему полного двоичного одноразрядного сумматора. Эта схема приведена на рисунке 14.8. Ее можно минимизировать, но это несколько усложняет принципы построения сумматоров, поэтому вопросы минимизации рассматриваться не будут.
Полный двоичный одноразрядный сумматор изображается на схемах как показано на рисунке 14.9.
Для того чтобы получить многоразрядный сумматор, достаточно соединить входы и выходы переносов соответствующих двоичных разрядов.
Поиск по сайту: |