 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Пример отладки и тестирования программыСтр 1 из 3Следующая ⇒
Лабораторная работа № 5. Отладка и тестирование программ. Библиотека MATLAB’а
В ходе выполнения двух предыдущих работ вам пришлось написать несколько несложных программ. Вероятно, вы обратили внимание, что на то, чтобы написать текст программы, потребовалось не очень много времени. Гораздо больше времени ушло на то, чтобы исправить ошибки и заставить программу работать правильно. Если в вашем случае это не так, значит, либо у вас все-таки уже есть опыт программирования, либо вы обладаете уникальными способностями. Если вы не обнаружили у себя уникальных способностей – это не причина для расстройства. Даже опытные программисты тратят на отладку своих программ больше времени, чем на их написание. Тестирование (испытание) программ необходимо для получения надежных, правильно работающих программ. Процедура доводки программ протекает обычно следующим образом. Сначала разрабатывается система тестов – наборов исходных данных, на которых следует проверить правильность работы программы. Результаты, которые должна выдать программа для каждого теста, необходимо определить до запуска программы. После этого начинается прогон тестов. Как правило, на одном из тестов (чаще всего уже на первом) программа выдает неправильные результаты. Или даже вообще останавливается, не получив никаких результатов. Обнаружив наличие ошибки, временно прекращаем тестирование и переходим к отладке. Отладка – это поиск причины получения ошибочных результатов и устранение этой причины. Обнаружив и устранив ошибку, мы вновь возвращаемся к прогону тестов. До следующих результатов. Таким образом, отладка и тестирование это взаимосвязанные, переплетающиеся процессы. При разработке больших программных комплексов программированием и составлением тестов занимаются разные люди. Нам, скорее всего, потребуется разрабатывать относительно несложные программы. И, как написание программ, так и их тестирование и отладку, придется выполнять самим. Как организовать этот процесс? Сначала составить тесты, а затем приступить к программированию? Или наоборот написать программу, а уже потом придумать для нее тесты? В принципе это дело вкуса. Могу порекомендовать такой подход:
Пример отладки и тестирования программы
Рассмотрим эти довольно абстрактные размышления на простом конкретном примере. Пусть перед нами стоит задача написать программу, вычисляющую периметр и площадь многоугольника. Программу следует оформить в виде m-файла-функции. Многоугольник описывается матрицей VERTEX размера
В качестве простого первого теста можно предложить прямоугольный равнобедренный треугольник. Очевидно, что периметр этого треугольника Для иллюстрации я подготовил следующий m-файл, в котором старательно наделал ряд ошибок
function [P,S] = polygon(VERTEX) % Вычисление периметра и площади многоугольника % Вход: % VERTEX(n,2) - матрица, содержащая координаты вершин многоугольнмка. % Каждая строка описывает одну вершину. % Первое число - абсцисса, второе - ордината. % Выход: % P - периметр % S - площадь
% 1. Вычисление периметра n = size(VERTEX,1); for i=1:n DX = VERTEX(i+1,1) - VERTEX(i,1); DX = VERTEX(i+1,2) - VERTEX(i,2); Dlina = sqrt(DX^2+DY*2); P = P + Dlina; end % i
% 2. Вычисление площади for i=1:n DX = VERTEX(i+1,1) - VERTEX(i,1); if DX>0 S = S - DX*(VERTEX(i,2+Vertex(i+1,2))); else S = S + DX*(VERTEX(i,2)+VERTEX(i+1,2)); end % i
end % polygon
Даже если вы видите все сделанные мной ошибки, постарайтесь их не исправлять, а скопировать файл таким, как он здесь приведен. Алгоритм программы предельно прост. Периметр многоугольника – это сумма длин всех сторон. А длина каждой стороны определяется по теореме Пифагора. Площадь многоугольника вычисляется как алгебраическая сумма площадей трапеций расположенных между сторонами многоугольника и осью абсцисс.
Итак, начинаем с того, что пробуем запустить подготовленный тест. Для того чтобы запустить этот тест можно в командной строке набрать команду: [P,S] = polygon([0 0; 1 0; 0 1]) То есть просто написать вызов функции, задав в скобках описание подготовленного многоугольника. Я, однако, рекомендую вам не полениться и написать простой вспомогательный файл для вызова отлаживаемой функции.
function dbgpolygon % Отладка функции POLYGON определения периметра и площади многоугольника % Тест № 1 VERT = [ 0 0; ... 1 0; ... 0 1 ];
% Вызов отлаживаемой функции [Perimeter,Area] = polygon(VERT) end % dbgpolygon
В чем выгода такого подхода. Во-первых, не придется несколько раз набирать одну и ту же команду. Во-вторых, после того, как этот первый тест будет успешно пройден, надо будет всего лишь заменить исходные данные. В остальном этот файл останется без изменений. Кстати, при переходе к очередному тесту не следует удалять данные предыдущего. Лучше просто их закомментировать (вставив символ % в начале строк). Тогда к концу тестирования в этом отладочном файле будет содержаться полная программа тестов. Замечание. Я оформил этот отладочный файл, как файл-функцию. В данном случае использование файла сценария также возможно. Для того чтобы переделать мой файл-функцию в файл-сценарий здесь достаточно вычеркнуть первую и последнюю строки. Я, однако, предпочитаю сам и советую другим отдавать предпочтение использованию функций. Дело в том, что, когда заканчивается выполнение функции, то память, отведенная под внутренние переменные функции освобождается. А при использовании сценария эти переменные остаются в памяти. То есть накапливается мусор, а мусор имеет свойство мешать работе. Итак, приступим к тестированию и выполним команду:
>> dbgpolygon ??? Undefined function or variable 'DY'.
Error in ==> polygon at 16 Dlina = sqrt(DX^2+DY*2);
Error in ==> dbgpolygon at 9 [Perimeter,Area] = polygon(VERT)
Как и ожидалось, получить правильный результат с первой попытки не удалось. Зато вместо результатов появилось сообщение о том, что именно не понравилось MATLAB’у в программе. Кстати сообщение очень ясное, хотя и на английском языке. Должен признаться, посмотрев на это сообщение, я по-хорошему позавидовал нынешнему поколению программистов. Когда я начинал программировать, тогдашние средства диагностики обычно выдавали туманное сообщение наподобие “PROGRAM INTERRUPT” и длинные шестнадцатеричные числа – содержимое регистров процессора в момент прерывания. Теперь же мы имеем дело с ясным сообщением: «Undefined function or variable 'DY'» (Неопределенная функция или переменная DY). Более того, MATLAB указывает файл и номер строки в этом файле, где проявилась сделанная ошибка. Теперь можно посмотреть текст файла polygon.m. Нетрудно убедиться, что действительно переменной DY (длина проекции стороны многоугольника на ось ординат) до 16-й строки не было присвоено никакого значения. В данном случае виновата опечатка: в 15-й строчке вместо DY мы по ошибке набрали DX. Исправьте ошибку. И, кроме того, отметьте очень важный момент. Диагностика MATLAB’а указала нам 16-ю строку – место, где ошибка проявилась. А найти источник ошибки – 15-ю строку и опечатку в ней мы должны самостоятельно. И еще одно замечание по поводу диагностического сообщения MATLAB’а. Обратите внимание, что в сообщении приводится стек программных модулей. То есть сначала указывается модуль, в котором произошло прерывание (polygon), затем функция, которая вызвала polygon, то есть dbgpolygon. Сейчас наша программа состоит всего из двух модулей, и поэтому данная информация может показаться не слишком важной. Но когда вам придется писать более сложные программы, состоящие, быть может, из нескольких десятков модулей, вы по достоинству оцените это качество диагностики MATLAB’а. Итак, запускаем исправленную программу и вновь получаем сообщение:
>> dbgpolygon ??? Undefined function or variable "P".
Error in ==> polygon at 17 P = P + Dlina;
Error in ==> dbgpolygon at 9 [Perimeter,Area] = polygon(VERT)
Вновь изучаем текст программы. Причина ошибки: мы собираемся накапливать в переменной P сумму длин сторон многоугольника. Но перед тем, как начать это накопление, надо сначала задать этой переменной начальное нулевое значение. То есть перед циклом надо вставить строчку: P = 0; Еще одно важное замечание. Накопление суммы используется и во второй части программы, где вычисляется площадь многоугольника. Следует проверить, нет ли аналогичной ошибки и в этом случае. Как видим, есть. Общий вывод: обнаружив одну ошибку, имеет смысл потратить некоторое время и проверить, нет ли аналогичной ошибки в других местах программы. Эта небольшая затрата времени, как правило, окупается значительной экономией времени в дальнейшем. После исправлений программа приобретает вид
function [P,S] = polygon(VERTEX) % Вычисление периметра и площади многоугольника % Вход: % VERTEX(n,2) - матрица, содержащая координаты вершин многоугольнмка. % Каждая строка описывает одну вершину. % Первое число - абсцисса, второе - ордината. % Выход: % P - периметр % S - площадь
% 1. Вычисление периметра n = size(VERTEX,1); P = 0; for i=1:n DX = VERTEX(i+1,1) - VERTEX(i,1); DY = VERTEX(i+1,2) - VERTEX(i,2); Dlina = sqrt(DX^2+DY*2); P = P + Dlina; end % i
% 2. Вычисление площади S = 0; for i=1:n DX = VERTEX(i+1,1) - VERTEX(i,1); if DX>0 S = S - DX*(VERTEX(i,2+Vertex(i+1,2))); else S = S + DX*(VERTEX(i,2)+VERTEX(i+1,2)); end % i
end % polygon
Однако вновь запустив тест, получаем вместо результата очередное сообщение об ошибке:
>> dbgpolygon ??? Attempted to access VERTEX(4,1); index out of bounds because size(VERTEX)=[3,2].
Error in ==> polygon at 15 DX = VERTEX(i+1,1) - VERTEX(i,1);
Error in ==> dbgpolygon at 9 [Perimeter,Area] = polygon(VERT)
Действительно, при последнем выполнении цикла
справедлива для всех сторон. Между тем последняя сторона соединяет
Кстати, аналогичная ошибка имеет место и в определении площади. Самый простой (но не единственный) способ исправить эту ошибку: в цикле обрабатывать стороны с первой по (n-1)-ю, а последнюю обработать отдельно. Очередной исправленный вариант программы:
function [P,S] = polygon(VERTEX) % Вычисление периметра и площади многоугольника % Вход: % VERTEX(n,2) - матрица, содержащая координаты вершин многоугольнмка. % Каждая строка описывает одну вершину. % Первое число - абсцисса, второе - ордината. % Выход: % P - периметр % S - площадь
% 1. Вычисление периметра n = size(VERTEX,1); P = 0; for i=1:n-1 DX = VERTEX(i+1,1) - VERTEX(i,1); DY = VERTEX(i+1,2) - VERTEX(i,2); Dlina = sqrt(DX^2+DY*2); P = P + Dlina; end % i DX = VERTEX(1,1) - VERTEX(n,1); % последняя сторона DY = VERTEX(1,2) - VERTEX(n,2); Dlina = sqrt(DX^2+DY*2); P = P + Dlina;
% 2. Вычисление площади S = 0; for i=1:n-1 DX = VERTEX(i+1,1) - VERTEX(i,1); if DX>0 S = S - DX*(VERTEX(i,2+Vertex(i+1,2))); else S = S + DX*(VERTEX(i,2)+VERTEX(i+1,2)); end % i DX = VERTEX(1,1) - VERTEX(n,1); if DX>0 S = S - DX*(VERTEX(n,2+Vertex(1,2))); else S = S + DX*(VERTEX(n,2)+VERTEX(1,2));
end % polygon
Вновь запускаем программу. И вновь сообщение об ошибке.
>> dbgpolygon ??? Error: File: polygon.m Line: 28 Column: 1 At least one END is missing: the statement may begin here.
Error in ==> dbgpolygon at 9 [Perimeter,Area] = polygon(VERT)
К сожалению, теперь сообщение не столь ясно, как в предыдущих случаях. Поэтому стоит обсудить эту ситуацию подробней. Пока из сообщения понятно только, что пропущен оператор END. Однако совет MATLAB’а вставить этот оператор после 28-й строки выглядит сомнительным. Дело в том, что MATLAB не может знать, что именно вы хотите делать в своей программе. И поэтому самое большее, что он может здесь для вас сделать – это предложить вариант устранения синтаксической ошибки. А вот соответствует ли этот вариант вашим замыслам, можете установить только вы сами. Поясню причину этой довольно типичной ошибки. Я, составляя эту программу, попытался изобразить неопытного программиста и «забыл» что при записи условного оператора каждому “if” должен соответствовать свой “end”. В результате логика программы оказалась нарушенной и MATLAB просто не смог приступить к ее выполнению. Общие выводы:
После исправления (добавления end-ов) программа приобретает вид:
function [P,S] = polygon(VERTEX) % Вычисление периметра и площади многоугольника % Вход: % VERTEX(n,2) - матрица, содержащая координаты вершин многоугольнмка. % Каждая строка описывает одну вершину. % Первое число - абсцисса, второе - ордината. % Выход: % P - периметр % S - площадь
% 1. Вычисление периметра n = size(VERTEX,1); P = 0; for i=1:n-1 DX = VERTEX(i+1,1) - VERTEX(i,1); DY = VERTEX(i+1,2) - VERTEX(i,2); Dlina = sqrt(DX^2+DY*2); P = P + Dlina; end % i DX = VERTEX(1,1) - VERTEX(n,1); % последняя сторона DY = VERTEX(1,2) - VERTEX(n,2); Dlina = sqrt(DX^2+DY*2); P = P + Dlina;
% 2. Вычисление площади S = 0; for i=1:n-1 DX = VERTEX(i+1,1) - VERTEX(i,1); if DX>0 S = S - DX*(VERTEX(i,2+Vertex(i+1,2))); else S = S + DX*(VERTEX(i,2)+VERTEX(i+1,2)); end end % i DX = VERTEX(1,1) - VERTEX(n,1); if DX>0 S = S - DX*(VERTEX(n,2+Vertex(1,2))); else S = S + DX*(VERTEX(n,2)+VERTEX(1,2)); end
end % polygon
Ну что? Все наконец? Увы, нет:
??? Undefined command/function 'Vertex'.
Error in ==> polygon at 30 S = S - DX*(VERTEX(i,2+Vertex(i+1,2)));
Error in ==> dbgpolygon at 9 [Perimeter,Area] = polygon(VERT)
Здесь, правда, ошибка видна сразу: по рассеянности для имени массива во втором случае были использованы строчные буквы. То есть MATLAB считает Vertex именем новой переменной. Исправим Vertex на VERTEX, и не забудем сделать это и в 37-й строке, где сделана такая же ошибка. Общие выводы:
И вот, наконец, запустив программу очередной раз, мы получаем результат: >> dbgpolygon
Perimeter = 2.7321 + 1.4142i
Area = -1
Правда, результат явно неправильный. Но не расстраивайтесь. Опытные программисты считают серьезным успехом сам факт получения каких-то результатов. Даже если они не верны. Однако ошибка налицо. Теперь в отличие от предыдущих ошибок о ее наличии говорит нам не диагностика MATLAB’а, а сам факт получения неправильного результата. Как искать ошибку. Вообще-то довольно эффективный путь – внимательно перечитать текст программы. Часто этого оказывается достаточно. Но если это не помогает – надо вводить отладочные печати. Как и куда? Здесь нам на помощь должен прийти знаменитый дедуктивный метод. В самом деле, мы имеем общий результат – неправильно вычисленное значение периметра. А надо найти конкретную частную причину получения этого результата. Ход рассуждений может быть следующим. Периметр – это сумма длин сторон. Поэтому логично посмотреть – правильно ли вычисляются эти длины. Вставим две строчки для отладочной печати сразу после вычисления длины. В целях экономии бумаги привожу только фрагмент файл polygon, относящийся к вычислению периметра
% 1. Вычисление периметра n = size(VERTEX,1); P = 0; for i=1:n-1 DX = VERTEX(i+1,1) - VERTEX(i,1); DY = VERTEX(i+1,2) - VERTEX(i,2); Dlina = sqrt(DX^2+DY*2); Dlina, pause P = P + Dlina; end % i DX = VERTEX(1,1) - VERTEX(n,1); % последняя сторона DY = VERTEX(1,2) - VERTEX(n,2); Dlina = sqrt(DX^2+DY*2); Dlina, pause P = P + Dlina;
Во вставленных строчках два оператора MATLAB’а. Первый оператор представляет собой простейшее арифметическое выражение, состоящее из одной единственной переменной. Поскольку после этого оператора нет точки с запятой, значение переменной будет выведено в командное окно MATLAB’а. Второй оператор pause приостанавливает работу программы. Чтобы продолжить выполнение достаточно нажать клавишу Enter. Вообще-то в операторе паузы здесь нет необходимости, но на мой взгляд удобней иметь возможность не спеша обдумать полученный результат. После запуска программы получаем следующий результат ее работы
>> dbgpolygon Dlina = Dlina = 1.7321 Dlina = 0 + 1.4142i Perimeter = 2.7321 + 1.4142i Area = -1 Думается, что этой информации уже достаточно, чтобы найти ошибку. В самом деле, мы видим, что длина первой стороны определена правильно, второй – неправильно, а для третьей и вовсе получена мнимая величина. Чем вторая и третья стороны отличаются от первой? Тем, что они имеют ненулевую проекцию на ось Y. Посмотрим, что в программе делается с этой проекцией. Да вот же ошибка Dlina = sqrt(DX^2+DY*2); При вычислении длины вместо возведения в квадрат DY умножается на 2. Исправляем ошибку (в двух местах), удаляем отладочные печати, запускаем программу
>> dbgpolygon Perimeter = 3.4142 Area = -1 Теперь периметр вычисляется правильно. А если бы мы не сумели разглядеть ошибку. Бывает такое, что не видишь вроде бы очевидных вещей. Тогда пришлось бы продолжить локализацию ошибки. Для этого можно было бы добавить отладочную печать проекций DX и DY. Тогда стало бы ясно, что проекции вычисляются правильно, а вот длина нет. Таким образом точно установлено, что ошибка содержится в строчке Dlina = sqrt(DX^2+DY*2); Ну а если, глядя на этот оператор, вы все-таки не можете понять, в чем эта ошибка заключается. Не часто, но такое бывает. Тогда надо продолжить локализацию ошибки. Для этого надо ввести отладочную печать операндов, входящих в это выражение, то есть DX^2, DY*2, pause Общий вывод: для локализации ошибки следует использовать отладочные печати
Теперь осталось отладить вычисление площади. Будем надеяться, что еще раз перечитав этот фрагмент:
% 2. Вычисление площади S = 0; for i=1:n-1 DX = VERTEX(i+1,1) - VERTEX(i,1); if DX>0 S = S - DX*(VERTEX(i,2+VERTEX(i+1,2))); else S = S + DX*(VERTEX(i,2)+VERTEX(i+1,2)); end end % i DX = VERTEX(1,1) - VERTEX(n,1); if DX>0 S = S - DX*(VERTEX(n,2+VERTEX(1,2))); else S = S + DX*(VERTEX(n,2)+VERTEX(1,2)); end
вы вспомните, что 1) площадь трапеции равна произведению высоты на полусумму оснований, а не на сумму 2) проекция стороны на ось X может быть и положительной и отрицательной, а высота в формуле площади трапеции только положительной. То есть высота – это абсолютная величина проекции DX Устраняем эти ошибки. Наша программа теперь имеет следующий вид.
function [P,S] = polygon(VERTEX) % Вычисление периметра и площади многоугольника % Вход: % VERTEX(n,2) - матрица, содержащая координаты вершин многоугольнмка. % Каждая строка описывает одну вершину. % Первое число - абсцисса, второе - ордината. % Выход: % P - периметр % S - площадь
% 1. Вычисление периметра n = size(VERTEX,1); P = 0; for i=1:n-1 DX = VERTEX(i+1,1) - VERTEX(i,1); DY = VERTEX(i+1,2) - VERTEX(i,2); Dlina = sqrt(DX^2+DY^2); P = P + Dlina; end % i DX = VERTEX(1,1) - VERTEX(n,1); % последняя сторона DY = VERTEX(1,2) - VERTEX(n,2); Dlina = sqrt(DX^2+DY^2); P = P + Dlina;
% 2. Вычисление площади S = 0; for i=1:n-1 DX = VERTEX(i+1,1) - VERTEX(i,1); if DX>0 S = S - 0.5*abs(DX)*(VERTEX(i,2+VERTEX(i+1,2))); else S = S + 0.5*abs(DX)*(VERTEX(i,2)+VERTEX(i+1,2)); end end % i DX = VERTEX(1,1) - VERTEX(n,1); if DX>0 S = S - 0.5*abs(DX)*(VERTEX(n,2+VERTEX(1,2))); else S = S + 0.5*abs(DX)*(VERTEX(n,2)+VERTEX(1,2)); end
end % polygon
Запускаем программу и получаем, наконец, правильный результат:
>> dbgpolygon Perimeter = 3.4142 Area = 0.5000
Значит ли это, что в программе нет ошибок? Увы, нет. Начинающим программистам свойственно заблуждаться, считая, что получение правильного результата для одного набора данных гарантирует правильную работу и для всех других наборов. Так что одного теста для проверки программы недостаточно. Кстати, тест, который был нами выбран нехорош. При подготовке данных для тестов следует избегать нулей и единиц. Использование этих чисел зачастую не дает проявиться скрытым дефектам программы. Что кстати произошло в нашем случае. Давайте изменим тест следующим образом
function dbgpolygon % Отладка функции POLYGON определения периметра и площади многоугольника % Тест № 1 %VERT = [ 0 0; ... % 1 0; ... % 0 1 ]; % Тест № 2 VERT = [ 2 3; ... 3 3; ... 2 4];
% Вызов отлаживаемой функции [Perimeter,Area] = polygon(VERT) end % dbgpolygon
То есть рассмотрим тот же треугольник, но смещенный по отношению к осям координат. Очевидно, результат должен быть тот же самый. Но, запустив программу, получаем сообщение об ошибке
>> dbgpolygon ??? Attempted to access VERTEX(1,5); index out of bounds because size(VERTEX)=[3,2].
Error in ==> polygon at 30 S = S - 0.5*abs(DX)*(VERTEX(i,2+VERTEX(i+1,2)));
Error in ==> dbgpolygon at 13 [Perimeter,Area] = polygon(VERT)
В данном случае ошибка очевидна. Неправильно расставлены скобки в выражении суммы оснований трапеции. Исправляем эту ошибку (в двух местах) S = S - 0.5*abs(DX)*(VERTEX(i,2)+VERTEX(i+1,2)); И запускаем программу
>> dbgpolygon Perimeter = 3.4142 Area = 0.5000
Теперь результат получен верный. Но тестирование на этом не должно заканчиваться. В то же время и проверить все возможные наборы данных мы не имеем возможности. Поэтому тестирование должно быть разумным. Для данной программы можно ограничиться рассмотрением 3-х, 4-х и 5-угольников. Координаты вершин при этом желательно не задавать целыми числами. Кроме того желательно проверить как программа справится с многоугольником, имеющим много сторон. Например, 64. Вручную вводить координаты вершин нет необходимости. Можно в программе dbgpolygon записать построение вершин для правильного многоугольника
% Тест № 3. Правильный многоугольник n=64; R = 2; delta=2*pi/n for i=1:n VERT(i,1) = R*cos(delta*(i-1)); VERT(i,2) = R*sin(delta*(i-1)); end
Очевидно, что в пределе площадь и периметр этого многоугольника должны стремиться к площади и длине описанной окружности.
Цель данного занятия – показать, что процесс отладки это методичный поиск ошибок в программе. Для достижения успеха не требуется каких-то догадок или озарений. С помощью отладочных печатей вы все более и более сужаете область программы, в которой находится ошибка. И, в конце концов, находите ошибочный оператор. Конечно, на одном примере невозможно показать все нюансы, которые могут возникать при отладке и тестировании программ. В следующих разделах приводятся некоторые советы, выработанные многолетней практикой программирования многих программистов. Некоторые из них будут полезны при выполнении контрольного задания
Отладка
Сначала несколько слов об отладчике MATLAB’а. В силу важности процесса отладки были предприняты меры по ее автоматизации. Практически все системы программирования в настоящее время снабжены многофункциональными отладчиками. Не является исключением и MATLAB. Собственно встроенный редактор, в котором вы набирали текст программы является одновременно и отладчиком. Возможности таких отладчиков весьма обширны. С его помощью можно задать пошаговое выполнение программы и отслеживать изменение переменных, устанавливать точки прерывания (breakpoins). Я сам, однако, предпочитаю при поиске ошибок использовать отладочные печати тех переменных и в тех местах, где это представляется нужным. Должен признаться, я опасался, что мое отношение к отладчикам – это проявление косности и отсталости. Однако, когда я готовил это пособие, я обнаружил, что аналогичной точки зрения придерживаются и признанные авторитеты программирования. «Одна из причин нашей нелюбви к отладчикам состоит в том, что бывает очень легко заблудиться в подробностях сложных структур данных и управляющих конструкций. Пошаговое выполнение программы, по нашему мнению, менее продуктивно, чем тщательное ее обдумывание и добавление операторов вывода или дополнительных проверок в критических местах кода. Перебор всех операторов по очереди отнимает больше времени, чем просмотр хорошо продуманного отладочного вывода» (Керниган, Пайк «Практика программирования», 2004) Это не значит, конечно, что отладчики совсем бесполезны. Так очень удобно выделение различным цветом разных элементов программы. Так синим цветом выделяются зарезервированные слова MATLAB’а (function, if, end и т.п.), зеленым – комментарии. Так если набирая заголовок функции, вы сделаете ошибку в слове function, то, увидев, что это слово не стало синим, вы сразу найдете ошибке и исправите ее, не тратя времени на прогон программы. В случае если в тексте обнаруживается явная синтаксическая ошибка, отладчик подчеркивает это место красной линией. Вновь появляется возможность исправить ошибку без прогонов программы. Советую также обратить внимание на правую линейку рамки отладчика. На ней напротив некоторых операторов появляются горизонтальные черточки. Если вы подведете курсор к одной из этих черточек, откроется всплывающее окно, в котором указывается номер строки, вызвавшей сомнения отладчика, а также в чем эти сомнения заключаются.
А теперь несколько практических советов 1. Множество ошибок связано с неправильным считыванием исходных данных. Поэтому необходимо проводить эхо-проверку вводимых данных. В нашем примере это означает, что по крайней мере при первом прогоне теста надо распечатать массив VERT сразу после го задания, чтобы убедиться в отсутствии опечаток. 2. Отладочные операторы не стоит удалять сразу после обнаружения и исправления ошибки. Лучше их закомментировать (символ % в начале строки). Не исключено, что они потребуются при очередных тестах 3. При использовании условных операторов часто встречаются такие ошибки: Неверное указание ветви алгоритма Неполный учет возможных условий 4. В операторах цикла встречаются такие ошибки Неправильное указание условий окончания цикла Неправильное указание числа повторений цикла Бесконечные или замкнутые циклы Не предусмотрено изменение счетчика цикла 5. В арифметических операциях чаще всего встречаются такие ошибки Использование неверных констант Неверное определение порядка действий Деление на нуль Извлечение квадратного корня из отрицательного числа 6. Можно порекомендовать вести учет своих ошибок. Для этого можно вести такую таблицу. Здесь для примера я начал ее заполнять в соответствии с ошибками, обнаруженными при отладке программы polygon.
Тестирование
Надо сразу сказать, что исчерпывающее тестирование невозможно. Известен классический пример. Пусть программа получает на входе два целых числа и в качестве результата выдает одно. Если для хранения чисел используются 32 бита, то различных комбинаций двух чисел может быть
И для 100% гарантии правильности программы их следовало бы проверить все. Что разумеется невозможно. Поэтому приходится ограниваться относительно небольшим количеством тестов. Сколько их должно быть? Есть хорошее правило. Тесты должны быть составлены так, чтобы в ходе тестирования каждый оператор программы выполнялся хотя бы один раз. Это важно при использовании условных операторов. Неаккуратно составленные тесты могут многократно проверять одну ветвь алгоритма и ни разу не заглянуть на другую. Там обычно и скрывается ошибка, которая проявит себя в самый неподходящий момент В каждом следующем тесте должен использоваться класс данных, отличный от предыдущего. В частности при отладке программы polygon не имеет смысла составлять тесты для обработки, скажем, десяти треугольников. Разумнее подготовить по одному тесту для треугольника, четырехугольника и многоугольника с большим количеством сторон. При подготовке цифровых тестовых данных избегайте использования чисел 0 и 1. Эти два числа обладают своеобразными свойствами и могут не выявить скрытую ошибку. Программу следует тестировать в нормальных, экстремальных и исключительных условиях. Что это значит, поясним на примере нашей программы polygon. Нормальным условием можно считать обработку обычного многоугольника, например с 4 или 5 сторонами. Экстремальные условия – обработка многоугольника с минимально возможным количеством сторон (треугольника) и многоугольника с очень большим количеством сторон. Что касается исключительных условий, то здесь надо сначала покритиковать нашу вроде бы уже отлаженную программу polygon. Дело в том, что программисты вообще-то пишут программы, которыми должны будут пользоваться другие люди. По известному правилу: «Все что может испортиться – портится», кто-нибудь обязательно обратится к вашей программе неправильно. Например, переменная VERTEX окажется не матрицей с двумя столбцами, а вектором или вообще скалярной величиной. И хотя вам, может быть, и удастся доказать такому пользователю свою правоту, но мнение о ваших программах, как о ненадежных, сложится. Хорошая программа должна проверять, что поступает на ее вход, и сообщать пользователю о его возможных ошибках. В частности, если доводить программу polygon до идеала, в ней надо предусмотреть проверку: 1) размеров входного массива (количество строк должно быть больше двух, а количество столбцов равно двум) 2) наличия в данных совпадающих вершин 3) наличия пересекающихся сторон
Поиск по сайту: |
, где n – количество вершин многоугольника. Каждая строка этой матрицы содержит координаты X и Y вершины многоугольника. Вершины перечисляются в матрице в порядке обхода многоугольника против часовой стрелки.
Результатом работы программы должны быть две величины: P – периметр и S – площадь многоугольника.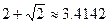
, а площадь ‑ 
.
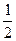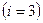при вычислении DX наша программа пытается использовать элемент матрицы VERTEX(4,1), в то время как эта матрица в нашем тесте содержит только три строки. Здесь допущена ошибка в алгоритме. Мы посчитали, что формулы для длин проекций стороны многоугольника: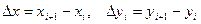
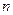-ю вершину не с 
-й, а с первой. То есть соответствующие формулы для последней стороны многоугольника будут:
