 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Умовна ймовірність та її властивістьСтр 1 из 2Следующая ⇒
Залежні та незалежні випадкові події Випадкові події А і В називають залежними, якщо поява однієї з них (А або В) впливає на ймовірність появи іншої. У противному разі випадкові події А і В називаються неза- Приклад 1. В урні міститься 10 однакових кульок, із них Розв’язання. Позначимо через А появу чорної кульки при першому вийманні, а через В — при другому. Випадкові події А і В будуть залежними, оскільки поява чорної кульки при першому її вийманні з урни (випадкова подія А) впливатиме на ймовірність появи чорної кульки (випадкова подія В) при другому вийманні. Приклад 2. З урни, де шість білих і чотири чорні кульки, вийняли дві кульки по одній, при цьому перша кулька в урну повертається. З’ясувати, чи будуть залежними такі події: перша виявиться чорною, друга також. Розв’язання. Нехай А — поява чорної кульки при першому вийманні, а В — при другому. Поява чорної кульки при першому вийманні (здійснилась подія А) не впливатиме на ймовірність поя- Умовна ймовірність та її властивість Якщо ймовірність випадкової події А обчислюється за умови, що подія В відбулася, то така ймовірність називається умовною. Ця ймовірність обчислюється за формулою
Аналогічно
1. Р (А / В) = 0, якщо А∩В = Æ. 2. Р (А / В) = 1, якщо А∩В = В. 3. У решті випадків 0 < Р(А / В) < 1. Приклад 1. Задана множина цілих чисел. Ώ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. Навмання беруть одне число. Яка ймовірність того, що це число виявиться кратним 3, коли відомо, що воно є непарним? Розв’язання. Нехай подія А — поява числа кратного 3, В — кратного 2. Тоді А = (3, 6, 9, 12), m1 = 4; В = (2, 4, 6, 8, 10, 12), m2 = 6; А∩В = (6, 12), m3= 2;
Оскільки Умовну ймовірність Р (А / В) для цієї задачі можна обчислити й інакше. За умовою задачі відомо, що взяте навмання число, є непарним, тобто в цьому разі ми дістали додаткову інформацію: із множини Ώ беруться лише непарні числа. Отже, простір елементарних подій тепер має вигляд
Елементарні події, що сприяють появі А, — появі числа, кратного 3, утворюють множину Отже,
Приклад 2. Відомі значення:
З’ясувати, чи є залежними випадкові події А і В. Розв’язання.
Оскільки 3. Формули множення ймовірностей Згідно із (17) і (18) маємо: Р (А ∩ В) = Р (В) Р (А / В) = Р (А) Р (В / А). (19) Формула множення для n залежних випадкових подій А1,А2, … А4: Р Приклад 1. У ящику міститься 15 однотипних деталей. Із них 9 стандартні, а решта — браковані. Деталі виймають по одній без повернення. Так було вийнято три деталі. Обчислити ймовірності таких випадкових подій: 1) А — три деталі виявляться стандартними; 2) В — усі три виявляться бракованими; 3) С — дві стандартні й одна бракована. Розв’язання. Нехай Аі — поява стандартної,
Оскільки випадкові події Аі, Р(А) = Р(А1∩А2∩А3) = Р(А1) Р(А2 / А1) Р(А3 / А1А2) =
Приклад 2. Із множини чисел Ω = {1, 2, 3, 4, 5, 6, 7, 8, 9} навмання беруть одне число, а далі з решти — друге. Яка ймовірність того, що здобуте двоцифрове число буде парним? Розв’язання. Позначимо через А1 — поява непарної цифри при першому вийманні, через В1 — поява парної цифри при першому, а через В2 — появу парної цифри при другому вийманні. Нехай С — випадкова подія: поява парного двоцифрового числа. Тоді С = (А1∩В2) È (В1∩В2). Оскільки випадкові події А1, В1, В2 є залежними, то Р (С) = Р (А1∩В2) È (В1∩В2) = Р(А1∩В2) + Р (В1∩В2) = = Р (А1) Р (В2 / А1) + Р (В1) Р (В2 / В1) = 4. Формули множення ймовірностей Якщо випадкові події А і В є незалежними, то Р(А / В) = Р(А), Р(В / А) = Р(В). Формули (19), (20) наберуть такого вигляду: Р(А∩В) = Р(А) Р(В); (21)
Приклад 1. Гральний кубик і монету підкидають по одному разу. Яка ймовірність того, що при цьому на грані кубика випаде число, кратне 3, а на монеті герб? Розв’язання. Нехай поява числа, кратного трьом — подія А, а поява герба — подія В. Випадкові події А і В є між собою незалежними. Отже,
Приклад 2. Три студенти складають на сесії екзамен з математики. Імовірність того, що перший складе екзамен, дорівнює 0,9, для другого та третього студентів ця ймовірність становить відповідно 0,8 і 0,7. Обчислити ймовірності таких випадкових подій: 1) А — три студенти складуть екзамен; 2) В — три студенти не складуть екзамену; 3) С — два студенти складуть екзамен. Розв’язання. Позначимо А1, А2, А3 — випадкові події, які полягають у тому, що перший, другий і третій студенти складуть екзамен з математики. Тоді Р(А1) = 0,9, Р(А2) = 0,8, Р(А3) = 0,7. Тоді ймовірності протилежних подій такі: Р( Р( Р(
Оскільки випадкові події Аі, Р(А) = Р(А1∩А2∩А3) = Р(А1) Р(А2) Р(А3) = 0,9 · 0,8 · 0,7 = 0,504; Р(В) = Р(
5. Імовірність появи випадкової
Нехай С — поява події Аі хоча б один раз при n незалежних спробах, тобто ця подія може з’явитися або один раз, або двічі, тричі і так далі, включаючи всі n раз. Тоді подія С і подія, яка полягає в тому, що при n спробах Аі не з’явиться жодного разу
Отже,
Якщо Р(Аі) = pі = p = const, то qі = q = const. Тоді Р(С) = 1 – qn. (24) Приклад 1. Прилад складається з чотирьох елементів, що працюють незалежно один від одного. Імовірність того, що перший елемент не вийде з ладу під час роботи приладу, є величиною сталою і дорівнює 0,95. Для другого, третього і четвертого елементів ця ймовірність дорівнює відповідно 0,9; 0,85; 0,8. Яка ймовірність того, що під час роботи приладу з ладу не вийде хоча б один елемент? Розв’язання. Нехай p1 = 0,95 — імовірність того, що перший елемент не вийде з ладу. Для другого, третього та четвертого елементів ця ймовірність становитиме відповідно p2 = 0,9; p3 = 0,85; p4 = 0,8. Імовірність того, що ці елементи вийдуть із ладу, дорівнюватиме відповідно: q1 = 1 – p1 = 1 – 0,95 = 0,05; q2 = 1 – p2 = 1 – 0,9 = 0,1; q3 = 1 – p3 = 1 – 0,85 = 0,15; q4 = 1 – p4 = 1 – 0,8 = 0,2. На підставі (23) маємо: Р(С) = 1 – q1 q2 q3 q4 = 1 – 0,05 × 0,1 × 0,15 × 0,2 = 1 – 0,00015 = 0,99985. Приклад 2. Гральний кубик підкидається чотири рази. Чому дорівнює ймовірність того, що цифра 3 з’явиться при цьому хоча б один раз? Розв’язання. Імовірність того, що при одному підкиданні з’явиться цифра 3, дорівнює Згідно з (24) дістанемо: Р(С) = 1 – q4 = 6. Використання формул теорії Оцінити надійність роботи системи, елементи якої з’єднані за схемою, наведеною на рис. 7.
Позначивши надійність системи через R, дістанемо
Оцінити надійність роботи системи, елементи якої з’єднані за схемою, наведеною на рис. 8.
Рис. 8
Приклад. Електричні лампочки з’єднані за схемами, наведеними на рис. 9 і 10.
Імовірність того, що електролампочка не перегорить при ввімкненні в електромережу наведених схем, є величиною сталою і дорівнює рі = 0,8. Яка ймовірність того, що при ввімкненні в електромережу наведених схем у них буде електрострум? Розв’язання. За відомим значенням рі знаходимо qі = 1 – рі = 1 – 0,8 = а) R =
Поиск по сайту: |
 ,
,  . (17)
. (17) ,
,  . (18)
. (18) ;
; 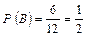 ;
;  ;
;  .
. , то події А і В є залежними.
, то події А і В є залежними.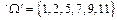 ,
,  .
. ,
, 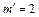 .
. .
. ;
; 




 .
. то випадкові події А і В є залежними.
то випадкові події А і В є залежними.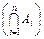 = Р (А1) Р(А2 / А1) Р(А3 / А1А2) … Р(Аn / А1А2 … Аn–1) (20)
= Р (А1) Р(А2 / А1) Р(А3 / А1А2) … Р(Аn / А1А2 … Аn–1) (20) — бракованої деталі при і-му вийманні.
— бракованої деталі при і-му вийманні.
 ,
,  ,
, .
.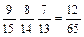 ;
;
 .
.


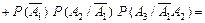
 .
. .
. . (22)
. (22)
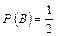 ;
;  .
. — відповідно не складуть. За умовою задачі маємо:
— відповідно не складуть. За умовою задачі маємо: ) = 1 – Р(А1) = 1 – 0,9 = 0,1;
) = 1 – Р(А1) = 1 – 0,9 = 0,1; ) = 1 – Р(А2) = 1 – 0,8 = 0,2;
) = 1 – Р(А2) = 1 – 0,8 = 0,2; ) = 1 – Р(А3) = 1 – 0,7 = 0,3
) = 1 – Р(А3) = 1 – 0,7 = 0,3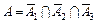 ,
, 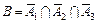 ,
, .
.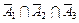 ) = Р(
) = Р(  ) Р(
) Р(  ) Р(
) Р(  ) = 0,1 · 0,2 · 0,3 = 0,006;
) = 0,1 · 0,2 · 0,3 = 0,006;



 .
. Нехай проводиться n незалежних спроб, у кожній з яких може відбутися подія Аі (і =1, 2, 3, ... n) з імовірністю Р(Аі) = pі або подія
Нехай проводиться n незалежних спроб, у кожній з яких може відбутися подія Аі (і =1, 2, 3, ... n) з імовірністю Р(Аі) = pі або подія 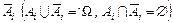 з імовірністю
з імовірністю  ,
,  .
. , утворюють повну групу, а саме:
, утворюють повну групу, а саме:  . При цьому
. При цьому  .
. ;
;
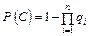 . (23)
. (23) . Тоді q = 1 – p = 1 –
. Тоді q = 1 – p = 1 –  .
.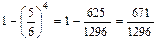 .
.
 Рис. 7
Рис. 7 . (25)
. (25)
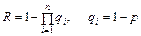 . (26)
. (26)

 ;
; б)
б)  .
.