 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Свойства средней арифметической. Средняя арифметическая обладает некоторыми математическими свойствами ⇐ ПредыдущаяСтр 2 из 2
Средняя арифметическая обладает некоторыми математическими свойствами, которые более полно раскрывают ее сущность и в ряде случаев упрощают ее расчеты. 1) Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты:
2) Если все варианты осредняемого признака уменьшить или увеличить на постоянное число А, то и средняя арифметическая соответственно уменьшиться или увеличиться на ту же величину А:
3) Если каждую варианту уменьшить или увеличить в А раз, то средняя арифметическая соответственно уменьшиться или увеличиться в А раз:
4) Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не измениться:
5) Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:
Другие виды средних
Помимо средней арифметической используются и другие виды средних величин, применение которых в каждом конкретном случае зависит от характера имеющихся данных. Средняя гармоническая применяется в том случае, если известен числитель, но неизвестен знаменатель ИСС. 1) Средняя гармоническая простая применяется, если объемы явлений равны:
Пример 2. Имеются данные о продаже товара на двух рынках города.
Средняя цена реализации товара
2) Средняя гармоническая взвешенная применяется в тех случаях, когда в качестве весов применяются произведения единиц совокупности на значения признака:
Пример 3. Имеются данные о продаже товара на двух рынках города.
Средняя цена реализации товара Средняя геометрическая получила широкое применение в анализе динамики для определения среднего темпа роста:
Наряду с рассматриваемыми средними величинами рассчитываются структурные средние – мода и медиана. Мода – это варианта (значение признака), наиболее часто встречающаяся в ряду распределения. а) Длядискретных вариационных рядов модой будет значение варианты с наибольшей частотой. Рассмотрим определение моды на примере 1а. Мо равна 4 годам стажа, б) В отличие от дискретных вариационных рядов определение моды в интервальном ряду осуществляется по следующей формуле:
где
Пример. Распределение семей города по размеру среднедушевого дохода в январе 1998 года:
Медиана – это варианта, находящаяся в центре упорядоченной по возрастанию значений признака совокупности. Медиана делит вариационный ряд на две равные части. При этом 50% единиц совокупности имеют значение меньше медианного, а 50% - больше медианного. а) для определения медианы в дискретных вариационных рядах сначала находят ее порядковый номер по формуле: NMe=(n+1)/2 где n - объем совокупности . Если n – четное число, то рассчитанная величина NMe будет дробным числом, например номер медианы, полученной по данным примера 1а NMe= (10+1)/2= 5,5. Тогда значение медианы рассчитывают, как среднюю арифметическую величину из значений х5 и х6. По накопленным частотам ищем значения х5 и х6, оба они равны 4. Таким образом, наша задача упрощается и находить их среднее значение не нужно : медиана =4 Если n – нечетное число, то медианой будет являться значение варианты непосредственно под медианным номером. б) В интервальных вариационных рядах сначала определяют медианный интервал. Для этого, как и в дискретных рядах, рассчитывают номер медианного значения, а затем по накопленной частоте находят, какому интервалу принадлежит медианное значение признака. За тем медиана интервального ряда распределения определяется по формуле:
где
Пример:
Если мода отражает наиболее распространенное значение признака, то медиана практически выполняет функции средней для неоднородной совокупности. Пример. Допустим, нам необходимо дать характеристику среднего дохода группы людей из 100 человек, 99 из которых имеют доход в интервале от 100 до 200 долл. в месяц, а месячный доход последнего человека из группы составляет 50000 долл.
Если мы воспользуемся формулой для средней арифметической, то получим средний доход, равный примерно 600-700 долл., который не только в несколько раз меньше дохода 100-го человека, но и имеет мало общего с доходами остальных членов группы. Медиана же, равная в данном случае 163 долл., позволит дать объективную характеристику уровня доходов 99% данной группы людей.
Поиск по сайту: |
 ;
;

 или
или 


 .
. руб.
руб. , тогда
, тогда  . Средняя гармоническая взвешенная имеет вид:
. Средняя гармоническая взвешенная имеет вид: .
. руб.
руб. (простая).
(простая).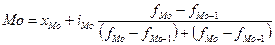 ,
, - нижняя граница модального интервала;
- нижняя граница модального интервала; - величина модального интервала;
- величина модального интервала; - частота модального интервала;
- частота модального интервала; - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному; - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным. руб.
руб. руб., т.е. половина семей города имеет среднедушевой доход менее 780 руб.
руб., т.е. половина семей города имеет среднедушевой доход менее 780 руб.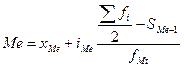 ,
, – нижняя граница значения интервала, содержащего медиану;
– нижняя граница значения интервала, содержащего медиану; – величина медианного интервала;
– величина медианного интервала; - сумма частот;
- сумма частот;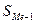 – сумма накопленных частот, предшествующих медианному интервалу;
– сумма накопленных частот, предшествующих медианному интервалу; – частота медианного интервала.
– частота медианного интервала.