 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Средняя арифметическая и ее свойстваСтр 1 из 2Следующая ⇒
Тема № 5 Средние величины Сущность и значение средних величин Средняя арифметическая и ее свойства Другие виды средних величин Сущность и значение средних величин
Наиболее распространенной формой статистических показателей, используемых в социально – экономических исследованиях, является средняя величина. Средняя величина – это обобщающий показатель, характеризующий общий уровень признака изучаемой совокупности в конкретных условиях места и времени. Показатель в форме средней величины отражает уровень варьирующего признака, отнесенный к единице совокупности. Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значения признаков отдельных единиц могут колебаться в ту или иную сторону под влиянием множества факторов, среди которых как основные так и случайные. Сущность вредней в том и заключается, что в ней взаимопогашаются индивидуальные различия единиц совокупности, обусловленные действием случайных факторов, и находят выражение то общее, что присуще всем единицам исследуемой совокупности, вызванное действием основных факторов. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам. Средняя только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности. Определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу:
Например, для расчета средней заработной платы работников предприятия необходимо общий фонд заработной платы разделить на число работников:
Многие формы средних величин относят к классу степенных средних:
где
Если k = 1, то имеем среднюю арифметическую; если k = -1, то среднюю гармоническую, а если k = 2, то среднюю квадратическую.
Средняя арифметическая и ее свойства
Наиболее распространенным видом средних величин является средняя арифметическая. Она применяется тогда, когда объем осредняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности. В зависимости от характера имеющихся данных средняя арифметическая может быть простой или взвешенной. 1) Cредняя арифметическая простая. Она применяется в тех случаях, когда каждое значение признака повторяется в совокупности один раз или когда данные не сгруппированы:
Пример 1. Вычислить средний стаж работы 10 сотрудников фирмы: 6, 5, 4, 3, 3, 4, 5, 4, 5, 4 лет, т. е. дан ряд одиночных значений признака, тогда
2) Cредняя арифметическая взвешенная. Она применяется в тех случаях, если каждое значение признака повторяется несколько раз.
Пример 1а. Построим ряд распределения сотрудников фирмы по стажу работы:
Средний стаж работы равен
Если частота выражена в процентах, то средняя арифметическая взвешенная определяется следующим образом:
где
Пример 1б. Для данного примера средний стаж равен:
Поиск по сайту: |


 ,
, - средняя величина исследуемого явления;
- средняя величина исследуемого явления; - i-тый вариант осредняемого признака;
- i-тый вариант осредняемого признака; - вес i-того варианта.
- вес i-того варианта.
 года.
года.
 )
)
 )
)
 года.
года. ,
, называется частостью.
называется частостью.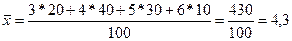 года.
года.