 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Критерии выбора вида средней в экономических расчетах ⇐ ПредыдущаяСтр 2 из 2
В экономических расчётах наиболее часто используют средние арифметические и средние гармонические. Выбор того или иного вида средней зависит от исходных данных и исходного отношения – логической (словесной) формулы средней. Исходное отношение составляются на основе теоретического и экономического анализа. Примеры составления исходных отношений таковы:
Далее используется критерии. 1. Если в исходном отношении известен числитель, т.е. его можно определить с помощью одного лишь суммирования, а знаменатель неизвестен, но его можно определить последовательно, на основе других известных величин, то следует применять среднюю гармоническую. 2. Если в исходном отношении известен знаменатель, т.е. его можно определить с помощью одного лишь суммирования, а числитель непосредственно неизвестен, но его можно последовательно определить, то следует использовать среднюю арифметическую. 3. Если в исходном отношении известен и числитель, и знаменатель, т.е. их можно определить последовательно путём простого суммирования, то используют среднюю в неявной форме – как отношение одного объёмного показателя к другому объёмному показателю. Другие виды средних величин. Средняя квадратическая: простая взвешенная Наиболее широко этот вид средней используется при расчёте показателей вариации. Аналогично можно получить среднюю кубическую, возведя значения признака в 3-ю степень и взяв корень 3-й степени. Средняя геометрическая: простая взвешенная Основное применение средняя геометрическая находит при определении среднего темпа роста. Все рассмотренные выше виды средних величин принадлежат к общему виду степенных средних. Степенная средняя степени k есть корень k-й степени из частного от деления суммы индивидуальных значений признака в k-й степени на число индивидуальных значений: простая взвешенная При
Структурные средние. При изучении вариации применяются и такие характеристики вариационного ряда, которые описывают количественную его структуру. Таковы медиана и мода. Медиана – это значение признака, делящее пополам ранжированный (упорядоченный) вариационный ряд. Одна половина значений больше медианы, а другая – меньше. Основное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины:
Определим медиану по несгруппированным данным. Предположим, что 7 сотрудников отдела имеют следующий стаж работы (лет): 5, 2, 4, 3, 4, 2, 2. Для определения медианы необходимо провести ранжирование: 2, 2, 2, 3, 4, 4, 5. Центральным в этом ряду является стаж 3 года, следовательно данный стаж и будет медианой. Если ранжированный ряд включает чётное число единиц, то медиана определяется как средняя из двух центральных значений. Для неоднородных совокупностей медиана практически выполняет функции средней. В этих случаях средняя не позволяет объективно оценить исследуемую совокупность вследствие сильного влияния аномальных максимальный или минимальных значений. Допустим, необходимо дать общую характеристику прибыли 10 малых предприятий области, из которых 9 имеют прибыль в интервале от 100 до 250 тыс. руб., а прибыль последнего за рассматриваемый период составила 10000 тыс. руб.:
Если мы воспользуемся средней арифметической, то получим среднюю прибыль, равную примерно 1150 тыс. руб., что не только почти в 9 раз меньше прибыли 10-го предприятия, но и имеет мало общего с финансовыми результатами деятельности остальной части предприятий. Медиана же, равная в данном случае 16 тыс. руб., позволит дать объективную характеристику уровня доходов 90% данной совокупности малых предприятий. Рассмотрим определение медианы по сгруппированным данным. Предположим, распределение торговых предприятий города по уровню розничных цен на товар А имеет следующий вид:
Для определения медианного значения признака по следующей формуле находят номер медианной единицы ряда:
где В нашем случае Полученное дробное значение, всегда имеющее место при чётном числе единиц в совокупности, указывает, что точная середина находится между 60-м и 61-м предприятиями. Необходимо определить к какой группе относятся предприятия с этими порядковыми номерами. Это можно сделать, рассчитав накопленные частоты. Магазинов с этими номерами нет в первой группе, где всего лишь 3 торговых предприятия, их нет ни во второй группе (3+18=21), ни в третьей группе (3+18+25=46). 60-е и 61-е предприятия находятся в четвёртой группе (3+18+25+31=77), следовательно медианой является цена 213 руб. В интервальном вариационном ряду для нахождения медианы применяется следующая формула:
где х0 – нижняя граница медианного интервала (первого интервала, накопленная частота которого превышает половину общей суммы частот); h – величина медианного интервала; mMe – частота медианного интервала. Пример. Имеются данные о дневной выработке 200 рабочих предприятий.
Требуется определить медиану дневной выработки рабочих предприятия.
70 – 80 – медианный интервал.
Мода – это значение изучаемого признака, которое встречается в изучаемой совокупности чаще всего, т.е. это признак с наибольшей частотой. В дискретном ряду мода определяется без вычисления как значение признака с наибольшей частотой.
mmax = 14 Mo = 4. Чаще встречаются ряды с одним модальным значением признака. Если два или несколько значений признака с наибольшей частотой имеются в вариационном ряду, он считается соответственно бимодальным, мультимодальным. В интервальном вариационном ряду для нахождения моды используют следующую формулу:
где h – величина модального интервала; mMo – частота модального интервала; mMo-1 – частота интервала, предшествующего модальному; mMo+-1 – частота интервала, следующего за модальным. Для нашего примера модальный интервал 80 – 90.
Поиск по сайту: |
 ,
, .
. ,
, .
. ,
, .
. ,
,
 получаем среднюю арифметическую, при
получаем среднюю арифметическую, при 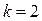 – квадратическую, при
– квадратическую, при  – кубическую, при
– кубическую, при  – геометрическую, при
– геометрическую, при  – гармоническую. Чем выше показатель степени k, тем больше значение средней величины. Если все исходные значения признака равны, то и все средние равны этой константе. Т.о., имеем следующее соотношение, которое называется правилом мажорантности средних:
– гармоническую. Чем выше показатель степени k, тем больше значение средней величины. Если все исходные значения признака равны, то и все средние равны этой константе. Т.о., имеем следующее соотношение, которое называется правилом мажорантности средних: .
.
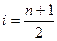 ,
, – объём совокупности.
– объём совокупности. .
. ,
, – накопленная частота интервала, предшествующего медианному;
– накопленная частота интервала, предшествующего медианному; дет.
дет. ,
, – нижняя граница модального интервала (имеющего наибольшую частоту);
– нижняя граница модального интервала (имеющего наибольшую частоту); .
.