 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Средняя арифметическая и её свойстваСтр 1 из 2Следующая ⇒
Тема 5. СРЕДНИЕ ВЕЛИЧИНЫ 1) Понятие средней величины 2) Средняя арифметическая и её свойства 3) Средняя гармоническая 4) Критерии выбора вида средней в экономических расчетах 5) Другие виды средних величин 6) Структурные средние Понятие средней величины. Наиболее распространённой формой статистических показателей, используемой в социально-экономических исследованиях, является средняя величина. Средняя величина – обобщающий показатель, выражающий типичный уровень (размер) варьирующего признака в расчёте на единицу однородной совокупности. Она отражает то общее, что складывается в каждой единице совокупности, улавливает общие черты, общие закономерности. Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные. Например, курс акций корпорации в целом определяется её финансовым положением. В то же время в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу. Сущность средней в том и заключается, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием основных факторов. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности. Если совокупность неоднородна, то общие средние должны быть заменены или дополнены групповыми средними, т.е. средними, рассчитанными по качественно однородным группам. Различают следующие виды средних величин: 1. средняя арифметическая; 2. средняя гармоническая; 3. средняя квадратическая; 4. средняя геометрическая; 5. средняя степенная; 6. структурные средние. В зависимости от характера имеющихся данных средняя величина может быть простой или взвешенной. Простые используются для несгруппированных данных, взвешенные – для сгруппированных данных. Средняя арифметическая и её свойства. Наиболее распространенным видом средних величин является средняя арифметическая. Простая средняя арифметическая:
где xi – значение варьирующего признака; n – число единиц совокупности. База для вычисления этой средней – первичные записи результатов наблюдений. Пример. Производственная деятельность трёх предприятий области, выпускающих один вид продукции, за месяц характеризуется следующими данными:
Требуется определить средний месячный объём производства в расчёте на одно предприятие.
При расчёте средних величин отдельные значения признака могут повторяться, встречаться по нескольку раз. В подобных случаях расчёт средней производится по сгруппированным данным, или вариационным рядам по формуле средней арифметической взвешенной:
где Если частота выражения в процентах, то
где fi – удельные веса, Пример. Объём производства и себестоимость продукции, производимой тремя предприятиями, характеризуются следующими данными:
Требуется определить среднюю себестоимость одного изделия.
Если при группировке значения осредняемого признака заданы интервалами, то при расчёте средней арифметической величины в качестве значения признака в группах принимают середины этих интервалов, т.е. исходят из гипотезы о равномерном распределении единиц совокупности по интервалу значений признака. Пример. Требуется определить средний размер кредита по следующим данным:
Свойства средней арифметической. 1. Алгебраическая сумма отклонений всех вариант от их средней арифметической равна нулю:
2. Сумма квадратов отклонений всех вариант от их средней арифметической меньше суммы квадратов отклонений вариант от любого другого числа
Рассмотрим правую часть
В правой части два положительных слагаемых, которые будут больше левой части 3. Средняя арифметическая алгебраической суммы нескольких варьирующих признаков равно алгебраической суммы средних арифметических этих признаков. Если
4. Если все варианты уменьшить или увеличить на одно и то же число а, то средняя арифметическая уменьшится или увеличится на а:
Польза этого свойства – можно сократить расчёты, если очень большие числа х: 1902, 1904, 1906, 1908, 1909 у: 0, 2, 4, 6, 7. а=1902. 5. Если все варианты увеличить или уменьшить в одно и то же число раз b, то и средняя увеличится или уменьшится в b раз:
6. Если все веса средней арифметической уменьшить или увеличить в k раз, то средняя арифметическая не изменится:
Если
Поиск по сайту: |
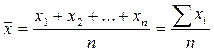 ,
,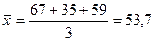 тыс. шт.
тыс. шт.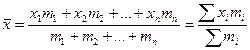 ,
,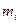 – частота или вес, показывает сколько раз встречается каждое i-е значение признака.
– частота или вес, показывает сколько раз встречается каждое i-е значение признака.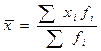 ,
,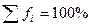 .
.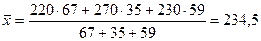 руб.
руб.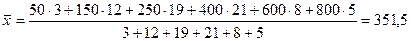 тыс. руб.
тыс. руб.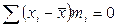 .
.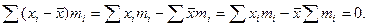
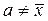 :
: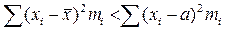 .
.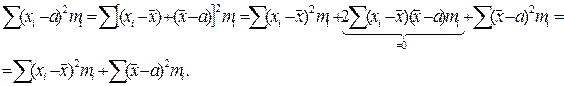
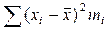 . Это свойство минимальности средней арифметической.
. Это свойство минимальности средней арифметической.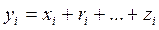 , то
, то 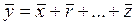 .
.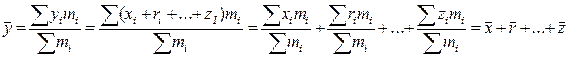 .
.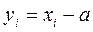 , то
, то 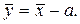

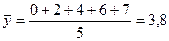
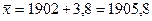 .
. , то
, то 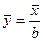 .
.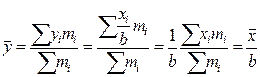 .
.
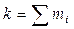 ,
, 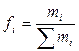 – относительная величина структуры.
– относительная величина структуры.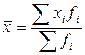 .
.