 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Средние отклонения от средних величин
Каждая статистическая величина от среднего значения отличается (отклоняется) по-разному и в любую сторону: со знаком плюс или минус. Поэтому для оценки типичности полученной средней величины надо знать величину среднего отклонения совокупности от нее. Поскольку неизбежны и отрицательные отдельные отклонения, необходима нейтрализация знака минус, иначе среднего отклонения не получится. Этого можно достичь двумя способами: принять отрицательные отклонения по модулю или возвести их во вторую степень (в квадрат). При первом способе образуется среднее линейное отклонение, а при втором — среднее квадратическое. В связи с тем, что средние величины могут быть простыми и взвешенными, аналогичными могут быть и средние отклонения. Поэтому среднее линейное отклонение определяется по формулам
В этих формулах прямые скобки означают, что разности или отклонения берутся по модулю, то есть без учета знака. Если ошибочно вместо прямых скобок принять обычные круглые, то получится Л=0. При использовании второго способа вначале определяется дисперсия отклонений по формулам
Дисперсия альтернативного признака (т.е. имеющего две взаимоисключающие разновидности, например, пол человека – мужской или женский, качество продукции – годная или бракованная) определяется по формуле 1.25, если вместо Xi подставить 1 и 0 (так как признак может принимать только 2 значения). Зная, что: p + q = 1, где p – доля единиц, обладающих признаком, q – доля единиц не обладающих им. Среднее значение можно найти по формуле (1.14):
Таким образом получим формулу дисперсии альтернативного признака, применив формулу (1.25):
Таким образом, дисперсия альтернативного признака равна
Предельное значение дисперсии альтернативного признака равно 0,25; оно получается при p = q = 0,5. В отличие от математики статистика оперирует не абстрактными, а смысловыми величинами, имеющими размерность. Поэтому и дисперсия здесь не безразмерная, как в математике, а сопровождается квадратической размерностью. Например, если статистическая величина измеряется в годах, или рублях, то дисперсия отклонений получится в «квадратных» годах или в «квадратных» рублях. Для получения обычной размерности находится среднее квадратическое отклонение («сигма»)как корень квадратный из дисперсии. То есть
Однако значения средних отклонений, как любой абсолютной величины, служат лишь количественной мерой анализа статистической совокупности. Для качественного анализа применяются относительные критерии, называемые коэффициентами вариации. Коэффициенты вариации Вариация — это несовпадение значений одной и той же статистической величины у разных объектов в силу особенностей их собственного развития, а также различия условий, в которых они находятся. Вариация имеет объективный характер и помогает познать сущность изучаемого явления. Если средняя величина сглаживает индивидуальные различия, то вариация, наоборот, их подчеркивает, устанавливая типичность или не типичность найденной средней величины для конкретной статистической совокупности. Тем самым можно делать вывод о качественности подобранных статистических данных. Вариация измеряется с помощью относительных величин, называемых коэффициентами вариации и определяемых в виде отношения среднего отклонения к средней величине. Поскольку среднее отклонение может определяться линейным и квадратическим способами, то соответствующими могут быть и коэффициенты вариации. Следовательно, коэффициенты вариации надо определять по формулам
Значения коэффициента вариации изменяются от 0 до 1 и чем ближе он к нулю, тем типичнее найденная средняя величина для изучаемой статистической совокупности, а значит и качественнее подобраны статистические данные. При этом критериальным значением коэффициента вариации служит 1/3. То есть средняя величина считается типичной для данной совокупности при λ Обычно квадратический коэффициент вариации несколько (примерно на 25%) больше линейного, рассчитанные по одним и тем же данным. А значит возможен случай, когда λ С помощью линейного коэффициента вариации принципиальный вывод о типичности или не типичности средней величины можно получить проще и быстрее, чем с помощью квадратического. Однако квадратический коэффициент применяется чаще, так как существует несколько способов для вычисления дисперсии. У такого способа оценки вариации есть и существенный недостаток. Действительно, пусть, например, исходная совокупность рабочих, имеющих средний стаж 15 лет, со стандартным отклонением σ = 10 лет, «состарилась» еще на 15 лет. Теперь Поэтому возможен дополнительный анализ статистической совокупности с помощью коэффициента осцилляции, определяемого по формуле
где R — размах вариации в виде разности наибольшего и наименьшего значений в совокупности статистических величин. То есть R = Хмах –Хmin, (1.31) где Xмax и Xmin — максимальное и минимальное значения в совокупности. При упорядочении статистических величин в совокупности образуются группировочные интервалы. Тогда под обозначением ∆Х понимается размах интервала, а среднее интервальное значение обозначается ХИ. В случае ориентировки только на квадратический коэффициент вариации могут применяться разные методы определения дисперсии.
Поиск по сайту: |

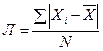 –простое;(1.22)
–простое;(1.22)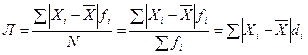 – взвешенное. (1.23)
– взвешенное. (1.23)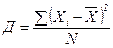 –простая;(1.24)
–простая;(1.24) – взвешенная.(1.25)
– взвешенная.(1.25) .
.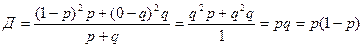 .
. . (1.26)
. (1.26) =
= 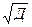 .(1.27)
.(1.27)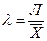 –линейный;(1.28)
–линейный;(1.28)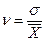 – квадратический.(1.29)
– квадратический.(1.29)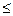 0,333 или при ν
0,333 или при ν 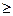 0,333, тогда необходимо взять среднюю из этих коэффициентов и по ее значению сделать окончательный вывод о не/типичности найденной средней величины.
0,333, тогда необходимо взять среднюю из этих коэффициентов и по ее значению сделать окончательный вывод о не/типичности найденной средней величины.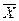 = 30 лет, а стандартное отклонение по-прежнему равно 10. Совокупность, ранее бывшая неоднородной (10/15*100 = 66,7%), со временем оказывается, таким образом, вполне однородной (10/30*100 = 33,3 %).
= 30 лет, а стандартное отклонение по-прежнему равно 10. Совокупность, ранее бывшая неоднородной (10/15*100 = 66,7%), со временем оказывается, таким образом, вполне однородной (10/30*100 = 33,3 %).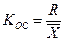 , (1.30)
, (1.30)