 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Особые виды степенных средних величин
Разновидностью простой средней арифметической служит средняя хронологическая величина, когда имеются моментные статистические величины на определенную одинаковую дату, например, на 1-е число каждого месяца в году. Формула средней хронологической теоретическому выводу не поддается и записывается приближенно в виде
где Х1 и Xn — первое и последнее значения статистической величины; Xi — промежуточные значения; n — общее число значений. По такой формуле бухгалтерия определяет среднегодовую стоимость основных фондов, учитывая ее значения на 1-е число каждого месяца. При этом n = 13, т. к. 1-е января фиксируется дважды: у отчетного и следующего за отчетным года. Аналогично коммерческие банки определяют среднегодовую сумму вкладов и выданных кредитов. Если учет квартальный, то n = 5. Средняя геометрическая величина получается при подстановке в формулу (1.11) m=0:
Для раскрытия неопределенностей этого вида прологарифмируем обе части формулы (1.11):
Подставляя в правую часть равенства m=0, получаем неопределенность вида
Следовательно, при m=0
Потенцируя, находим
Формула (1.18) является формулой средней геометрической простой, а если использовать частоты f, получим формулу средней геометрической взвешенной:
где П—символ произведения. Средняя геометрическая величина применяется, если задана последовательность индексов динамики, указывающих, например, на изменение уровня производства каждого последующего года по сравнению с предыдущим. Рассчитанные для одних и тех же данных различные средние величины оказываются неодинаковыми. Здесь действует правило мажорантности средних величин (впервые сформулировал профессор А. Я. Боярский), согласно которому с ростом показателя степени m в общих формулах увеличивается и средняя величина. То есть
Это правило частично подтвердилось расчетом средней себестоимости продукции, где средняя гармоническая получилась равной 4,1 руб./ед., а средняя арифметическая 4,3 руб./ед. Если рассчитать еще и среднюю геометрическую взвешенную, то она будет равной 4,2 руб./ед. Структурные средние Особый вид средних величин – структурные средние – применяется для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным ее расчет не может быть выполнен. В качестве структурных средних чаще всего используют показатели моды – наиболее часто повторяющегося значения признака – и медианы – величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. В итоге у одной половины единиц совокупности значение признака больше медианного уровня, а у другой – меньше его. Если изучаемый признак имеет дискретные значения, то особых сложностей при расчете моды и медианы не бывает. Если же данные о значениях признака Х представлены в виде упорядоченных интервалов его изменения (интервальных рядов), расчет моды и медианы несколько усложняется. Поскольку медианное значение делит всю совокупность на две равные по численности части, оно оказывается в каком-то из интервалов признака X. С помощью интерполяции в этом медианном интервале находят значение медианы:
где XMe – нижняя граница медианного интервала; ∆X – его величина (размах); ∑f/2 – половина от общего числа величин; fMe – число наблюдений или объем взвешивающего признака в медианном интервале. При расчете модального значения признака по данным интервального ряда надо обращать внимание на то, чтобы интервалы были одинаковыми, поскольку от этого зависит показатель повторяемости значений признака X. Для интервального ряда с равными интервалами величина моды определяется как
где ХMo – нижнее значение модального интервала; fMo – число наблюдений или объем взвешивающего признака в модальном интервале; fMo-1 – то же для интервала, предшествующего модальному; fMo+1 – то же для интервала, следующего за модальным; ∆X – величина интервала изменения признака в группах. Очевидно, что в формуле (1.20) и (1.21) можно заменить частоты f на доли d, так как Показателями типа медианы, характеризующими структуру рядов распределения признака, являются квартили (делят ряд на 4 равные части), квинтили (на 5), децили (на 10), перцентили (на 100).
Поиск по сайту: |
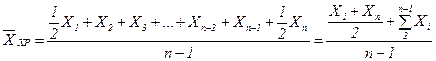 . (1.17)
. (1.17)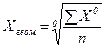 =
= 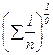 =
= 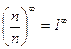
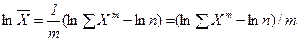 .
.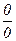 . Используя правило Лопиталя и дифференцируя отдельно числитель и знаменатель по переменной m, получаем
. Используя правило Лопиталя и дифференцируя отдельно числитель и знаменатель по переменной m, получаем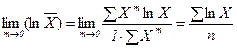 .
.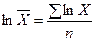 .
.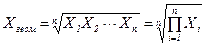 . (1.18)
. (1.18) =
=  – взвешенная,(1.19)
– взвешенная,(1.19)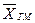 <
<  <
<  <
< 
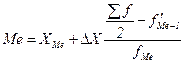 , (1.20)
, (1.20)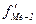 – сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала;
– сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала; , (1.21)
, (1.21)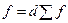 , а
, а 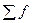 можно вынести за скобки как в числителе, так и в знаменателе и сократить.
можно вынести за скобки как в числителе, так и в знаменателе и сократить.