 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Векторна алгебра, елементи лінійної алгебри ⇐ ПредыдущаяСтр 2 из 2
Обов’язкові завдання: 2.1, 2.2, 2.5, 2.6, 2.10, 2.11, 2.13, 2.14, 2.18, 2.20, 2.21.
Завдання 2.1.Задані дві координати X і Y вектора 1. X=4; Y= 2. X=–4; Y=4; Задані точки А і В. Знайти координати векторів 5. A(–2; –7;3)і B(3; –1;10). 6. A(–7;2; –4) і B(–2;8;3). 7. A(3; –5; –2)і B(8;1;5). Визначити точку N, з якою співпадає кінець вектора 8. 10. Заданий модуль вектора 11. 13. Обчислити напрямні косинуси вектора 15. 17. Визначити, чи може вектор з координатними осями складати слідуючи кути. 19. 21. Вектор 23. 25. Вектор 27. 29.
Завдання 2.2.Вектори
1. 3. 5. Задані модулі векторів 7. 9. 11. Вектори 13. 16. Задані модулі векторів 19. 21. 23. Визначити 25. 27. 29.
Завдання 2.3.Перевірити колінеарність векторів 1. 3. 5. 7. Перевірити, чи слугують чотири точки А, В, С і D вершинами трапеції. 9. А( 6; –5; –3), В(–10; 3; 1), С( 7;–1; 6), D( 40; –13; 7). 10. А( 3; 4; –6), В( 9; –1; 2), С( 0; 2; –2), D( 30; –5; 6). 11. А( 2; 3; –10), В( 7; –5; 10), С( –3; 5;–14), D( 7; –2; 2). 12. А( –7; 1;–2), В( 20; 3; –7), С(–10; 9; 8), D( 3; –1; –7). 13. А( 6; 3; –2), В( 10; 5; –6), С( –16; –3; 4), D( –7; –1; 3). 14. А( –1; –7; 8), В( 7;–1; –4), С( 5; –6; –1), D( 5; 8; –1). 15. А( –2; –5; 5), В(10; 3; –3), С(1; 5;–2), D(–20; –1; 7). Визначити, при яких значеннях α і β вектори 16. 17. 18. 19. 20. 21. 22. 23. Задані точки А, В, С і D. Перевірити, чи колінеарні вектори 24. А(–3;6;5), В(7;40;–13), С(1;–10;3), D(6;7;–1). 25. А(–6;3;4), В(6;30;–5), С(2;9;–1), D(–2;0;2). 26. А(–10;2;3), В(2;7;–2), С(10;7;–5), D(–14;–3;5). 27. А(–2;–7;1), В(–7;3;–1), С(–7;20;3), D(8;–10;9). 28. А(–2;6;3), В(3;–7;–1), С(–6;10;5), D(4;–16;–3). 29. А(8;–1;–7), В(–1;5;8), С(–4;7;–1), D(–1;5;–6). 30. А(5;–2;–5), В(7;–20;–1), С(–3;10;3), D(–2;1;5). Завдання 2.4.Визначити модулі суми і різниці векторів 1. 3. 5. 7. 9. 11. 13. 15. 17. 19. 21. 23. 25. 27. 29. Завдання 2.5.Задано розкладання вектора 1. 3. 5. 7. 9. 11. 13 15 17. 19. 21. 23. 25. 27. 29. Завдання 2.6.Задано чотири вектора 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
Завдання 2.7.Знайти орт вектора
1. 4. 7. 10. 13. 16. 19. 22. 25. 28. Завдання 2.8.
1. У трикутнику АВС
2. У паралелограмі АВСD
3. У ромбі АВСD
4.У трикутнику АВС
5. У трапеції ABCD
6. У трикутнику АВС
7. У трапеції ABCD
8. У ромбі АВСD через вектори (DК
9. У рівнобедреному трикутнику АВС D
10. У трапеції ABCD
11. У трапеції ABCD
вектор
12. У трапеції ABCD Виразити через вектори
13. У трапеції ABCD
14. У трикутнику АВС
15. У трапеції АВСD
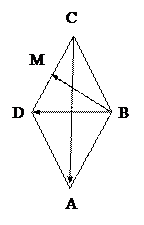
16. У трикутнику АВС
17. У трапеції АВСD
18. У трикутнику АВС
19. У трапеції АВСD
20. У ромбі АВСD (АМ ┴ ВС, М
21. У трапеції АВСD
22. У трикутнику АВС та
23. У паралелограмі АВСD
24. У трапеції АВСD
25. У трикутнику АВС
26. У трикутнику АВС
27. У паралелограмі АВСD
28. У ромбі АВСD
29. У трикутнику АВС
30. У трапеції АВСD
Завдання 2.9. Задані розкладання векторів 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
Завдання 2.10. Обчислити, яку роботу виконує сила 1. 2. 3. 4. 5. 6.
Поиск по сайту: |
 . Визначити його третю координату Z, якщо відомий модуль вектора
. Визначити його третю координату Z, якщо відомий модуль вектора  ;
; 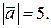 3. X=6; Y=–2;
3. X=6; Y=–2; 
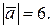 4. X=
4. X= 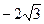 ; Y=6;
; Y=6; 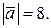
 і
і  .
.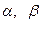 і
і  . Обчислити проекції вектора
. Обчислити проекції вектора  12.
12. 
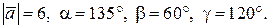 14.
14. 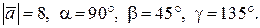
 ; 4).
; 4). 20.
20. 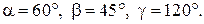
 22.
22. 
 та
та 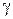 . Який кут він складає з віссю OY?
. Який кут він складає з віссю OY? 24.
24. 
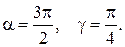 26.
26. 
 . Обчислити координати вектора
. Обчислити координати вектора 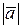 =2.
=2. 28.
28. 
 30.
30. 
 створюють кут
створюють кут  . Визначити
. Визначити  та
та 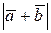 , якщо відомі модулі векторів
, якщо відомі модулі векторів  2.
2. 
 4.
4. 
 6.
6. 
 8.
8. 
 10.
10. 
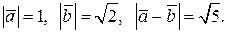 12.
12. 
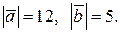 14.
14.  15.
15. 
 17.
17. 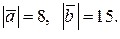 18.
18. 
 . Визначити
. Визначити  20.
20. 
 22.
22. 
 24.
24. 
 26.
26. 
 28.
28. 
 30.
30. 
 ;
;  .
. ;
;  .
. ;
;  .
.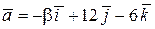 ;
; 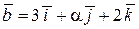 .
. ;
;  .
. ;
;  .
.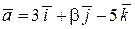 ;
;  .
. ;
;  .
. та
та  ; встановити, який з них довше другого і у скільки раз; як вони направлені – в одну або в різні сторони.
; встановити, який з них довше другого і у скільки раз; як вони направлені – в одну або в різні сторони.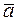 =(5;1;–4),
=(5;1;–4), 
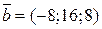 . 18.
. 18. 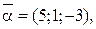
 .
.
 . 20.
. 20. 


 . 22.
. 22. 

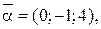
 . 24.
. 24. 


 . 26.
. 26. 


 . 28.
. 28. 


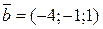 . 30.
. 30. 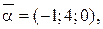

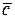 за базисом
за базисом 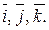 Визначити розкладання за цим базисом вектора
Визначити розкладання за цим базисом вектора  , паралельного вектору
, паралельного вектору 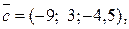
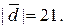 2.
2. 
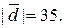

 4.
4. 


 6.
6. 


 8.
8. 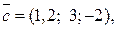

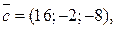
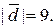 10.
10. 

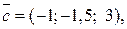



 14.
14. 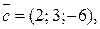
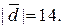

 16.
16. 

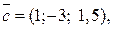






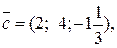
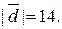







 та
та  . Знайти розвинення вектора
. Знайти розвинення вектора  за базисом
за базисом 




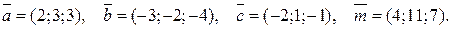
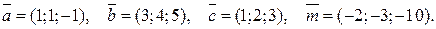







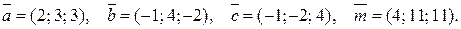




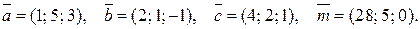

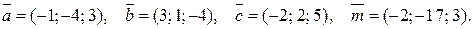




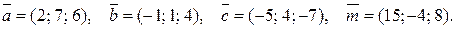


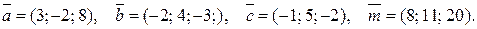
 .
. 2.
2. 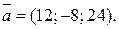 3.
3. 
 5.
5.  6.
6. 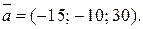
 8.
8.  9.
9. 
 11.
11. 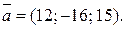 12.
12. 
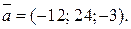 14.
14. 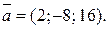 15.
15. 
 17.
17.  18.
18. 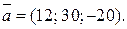
 20.
20.  21.
21. 
 23.
23.  24.
24. 
 26.
26.  27.
27. 
 29.
29.  30.
30. 

 Виразити через вектори
Виразити через вектори  та
та  вектор
вектор 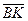 (ВК
(ВК  АС, К
АС, К  АС).
АС).
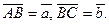 Виразити через вектори
Виразити через вектори  (DK
(DK 
 Виразити через вектори
Виразити через вектори  (АК
(АК 
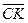 (СК
(СК 
 Виразити через вектори
Виразити через вектори 
 Виразити через вектори
Виразити через вектори 
 Виразити через вектори
Виразити через вектори 
 Виразити
Виразити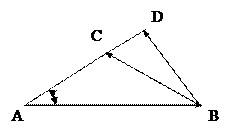
 о,
о,  Виразити через вектори
Виразити через вектори  (ВD
(ВD 
 ,
,  Виразити через вектори
Виразити через вектори  .
.
 ,
, Виразити через вектори
Виразити через вектори  .
.
 ,
, 


 ,
,  Виразити через вектори
Виразити через вектори  вектор
вектор 

 о,
о,  Виразити через вектори
Виразити через вектори  (ВN
(ВN 
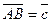 ,
,  ,
,  . Виразити через вектори
. Виразити через вектори 
 ,
,  ,
,  . Виразити через вектори
. Виразити через вектори 
 ,
, 
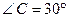 ,
,  . Виразити через вектори
. Виразити через вектори 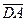 (DА ┴ ВС, D
(DА ┴ ВС, D 
 ,
,  ,
,  . Виразити через вектори
. Виразити через вектори 
 ,
, 

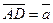 ,
,  ,
,  . Виразити через вектори
. Виразити через вектори 
 ,
,  ,
,  (СМ ┴ АВ, М
(СМ ┴ АВ, М 
 ,
, 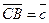 . Виразити через вектори
. Виразити через вектори 
 ,
,  . Виразити через вектори
. Виразити через вектори  (DА ┴ АВ).
(DА ┴ АВ).
 ,
, 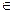 ВС).
ВС).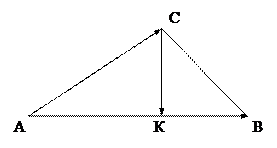
 ,
, 
 ,
, 
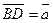 ,
, 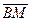 (ВМ ┴ DC, М
(ВМ ┴ DC, М 

 (DМ ┴ АВ, М
(DМ ┴ АВ, М  , які слугують сторонами трикутника, за двома взаємно перпендикулярними ортами. Обчислити довжину медіани
, які слугують сторонами трикутника, за двома взаємно перпендикулярними ортами. Обчислити довжину медіани  та висоти
та висоти  трикутника ABC.
трикутника ABC.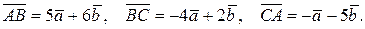








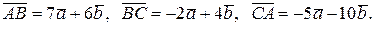




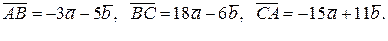
















 , коли її точка прикладення, що рухається прямолінійно, переміщується з положення А в положення В.
, коли її точка прикладення, що рухається прямолінійно, переміщується з положення А в положення В.