 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ЕЛЕМЕНТИ ЛІНІЙНОЇ ТА ВЕКТОРНОЇ АЛГЕБРИСтр 1 из 2Следующая ⇒
РОЗРАХУНКОВЕ ЗАВДАННЯ І СЕМЕСТРУ ЗМІСТОВНИЙ МОДУЛЬ № 1 ЕЛЕМЕНТИ ЛІНІЙНОЇ ТА ВЕКТОРНОЇ АЛГЕБРИ
Визначники, матриці, системи лінійних рівнянь. Обов’язкові завдання: 1.1, 1.3, 1.4, 1.6, 1.10, 1.12, 1.13.
Завдання 1.1. Розв’язати рівняння.
1.
4.
7.
10.
13.
16.
19.
22.
25.
28.
Завдання 1.2.Розв’язати нерівність, використовуючи властивості визначника.
1.
3.
5.
7.
9.
11.
13.
15.
17.
19.
21.
23.
25.
27.
29. Завдання 1.3.Обчислити визначник четвертого порядку: а) розклавши за елементами довільного ряду; б) використовуючи властивості визначника. 1. 4. 7. 10. 13. 16. 19. 22. 25. 28.
Завдання 1.4. Виконати дії над матрицями, якщо:
1. 3. 5. 7. 9.
11. 13. 15. 17. 19.
21. 23. 25. 27. 29.
Завдання 1.5.Знайти значення многочлена 1. 4. 7. 10. ; 13. 16. 19. 22. 25. 28.
Завдання 1.6.Розв’язати матричне рівняння:
1. 3. 5. 7. 9. 11. 13. 15. 17. 19. 21. 23. 25. 27. 29.
Завдання 1.7. За допомогою елементарних перетворень визначити ранг матриці.
1.
3.
5.
7.
9.
11.
13.
15.
17.
19.
21.
23.
25.
27.
29.
Завдання 1.8. Керівник митниці уклав договір на ремонт приміщень різних призначень
де Визначити на мові матриць: 1) загальну кількість кожного матеріалу і робочої сили на всі приміщення 2) вартість ремонту одного приміщення кожного типу; 3) загальна вартість ремонту всіх приміщень за типами; 4) вартість ремонту всіх типів приміщень; 5) вартість кожного виду матеріалів і робочої сили, потрібних на ремонт всіх приміщень.
1. А = B = (1 2 3); B = ( 1 2 2); B = ( 3 1 2); C = (5 6 12 13). C = (3 6 10 13). C = (1 6 8 10).
4. А = B = (1 2 3); B = (1 2 2); B = (3 1 2); C = (5 6 12 7). C = (3 6 10 4). C = (1 6 8 13).
7. А = B = (1 2 3); B = (1 2 2); B = (3 1 2); C = (5 6 12 13). C = (3,6,10,13). C = (1 6 8 10).
10. А = B = (1 2 3); B = (1 2 2); B = (3 1 2); C = (5 6 12 13). C = (3 6 10 13). C=(1 6 8 10).
13. А = B = (1 2 5); B = (1 2 6); B = (3 1 2). C = (5 6 8 7). C = (3 4 8 10). C = (1 6 9 10).
16. А = B = (1 2 3); B = (1 2 2); B = (3 1 2); C = (5 6 12 13). C = (3 6 10 13). C = (1 6 8 10).
19. А = B = (1 2 3); B = (1 2 2); B = (3 1 2); C = (5 6 12 13). C = (3 6 10 13) C = (1 6 8 10).
22. А = B = (1 2 3); B = (1 2 2); B = (3 1 2); C = (5 6 12 13). C = (3 6 10 13). C = (1 6 8 10).
25. А = B = (1 2 3); B = (1 2 2); B = (3 1 2); C = (5 6 12 13). C = (3 6 10 13). C = (4 6 8 10).
28. А = B = (1 2 3); B = (1 2 2); B = (3 1 2); C = (5 6 12 13). C=(3,6,10,15). C = (1 6 8 11).
Завдання 1.9. Для виробництва продукції типів
де Вартості одиниці кожного типу сировини (грошові одиниці) подаються матрицею-рядком 1) кількість сировини кожного типу, яка потрібна для виконання плану; 2) вартість сировини всіх типів, яка потрібна на одиницю виробу кожного типу; 3) вартість кожного виду сировини, яка необхідна на весь план; 4) вартість усієї сировини, яка необхідна для виконання плану.
1. P = (10 12 15 9); P = (7 2 3 5); P = (9 8 7 10); C = (2 3 1,3). C = (1 2 1 3). C = (2 2 1 3).
4. P = (5 12 15 9); P = (1 2 3 5); P = (2 8 7 10); C = (2 3 1 9). C = (1 2 8 3). C = (2 2 6 3).
7. P = (4 12 5 9); P = (7 2 3 5); P = (3 8 7 1); C = (2 3 1 3). C = (1 2 1 13). C = (12 2 1 3).
10. P = (10 12 15 9); P = (2 2 13 5); P = (9 8 7 10); C = (2 3 1 3). C=(1,2,1,3). C=(2 12 1 3).
13. P = (5 12 15 9); P = (1 2 7 5); P = (2 4 7 10); C = (2 3 1 9). C = (10 2 8 3). C=(2,12,6,3).
16. P = (1 2 5 19); P = (7 12 3 5); P = (3 3 7 1); C = (2 3 1 3). C = (1 2 7 13). C = (2 2 1 3).
19. P = (10 12 15 9); P = (7 2 3 5); P = (9 8 7 10); C = (2 3 1 3). C = (1 2 1 3). C = (2 2 1 3).
22. P = (5 12 15 9); P = (1 2 3 5); P = (2 8 7 10); C = (2 3 1 9). C = (6 2 4 3). C = (1 2 6 3).
25. P = (10 12 15 9); P = (7 2 3 5); P = (9 8 7 10); C = (2 3 1 3). C=(1,2,1,3). C=(2,2,1,3).
28. P = (5 12 15 9); P = (1 2 3 5); P = (2 8 7 10); C = (2 3 1 9). C = (1 2 8 3). C = (2 2 6 3).
Завдання 1.10. Дослідити систему рівнянь. Розв’язати систему рівнянь: а) за правилом Крамера; б) матричним способом; в) за методом Гаусcа. 1. 3. 5. 7. 9. 11. 13. 15. 17. 19. 21. 23. 25. 27. 29.
Завдання 1.11. Дослідити системи лінійних рівнянь на сумісність методом жорданових виключень та у разі сумісності знайти їх загальний розв’язок. Для однорідної системи побудувати фундаментальну систему розв’язків.
1. а)
2. а)
3. а)
4. а)
5. а)
6. а)
7. а)
8. а)
9. а)
10. а)
11. а)
12. а)
13. а)
14. а)
15. а)
16. а)
17. а)
18. а)
19. а)
20. а)
21. а)
22. а)
23. а)
24. а)
25. а)
26. а)
27. а)
28. а)
29. а)
30. а) Завдання 1.12.Визначити, при яких значеннях a система однорідних рівнянь має: 1) єдиний розв’язок; 2) множину розв’язків. Знайти розв’язки. 1. 3. 5. 7. 9. 11. 13. 15. 17. 19. 21. 23. 25. 27. 29.
Завдання 1. 13. 1. Встановлено, що витрати W(x) на обробку митних документів різних призначень Dk у кількості відповідно хk задовольняють закономірності
2. З деякого листового матеріалу треба розкроїти b1 заготовок типу А, b2 – типу В, b3 – типу С. При цьому можна розкроїти трьома способами. Кількість заготовок кожного листа за кожним способом розкрою зазначено в таблиці. Скільки листів потрібно розкроювати кожним способом розкрою?
3. Для виробництва трьох видів товарів Т1, Т2, Т3 використовується три типи ресурсів Р1, Р2, Р3. Кількість одиниць кожного ресурсу, для виробництва кожного товару, а також запаси кожного ресурсу подано в таблиці. Знайти кількість товарів кожного виду, які можна виробити за умови використання всього запасу ресурсів.
4. З пункту А в пункт В треба перевезти обладнання 3-х типів: В1 – b1 од., B2 − b2 од., B3 − b3 од. на трьох видах транспорту. Кількість обладнання кожного типу, яке можна розмістити в одиниці певного транспорту, наведено в таблиці. Скільки треба транспортних одиниць кожного виду для перевезення всього обладнання?
5. Підприємство складається з трьох цехів, у кожному з яких виробляють відповідний (один) вид продукції. У кожному цеху на потреби виробництва використовують продукцію всіх цехів цього підприємства (
6. Установлено, що витрати W(x) на обробку митних документів різних призначень Dk у кількості відповідно хk задовольняють закономірності
7. .З деякого листового матеріалу треба розкроїти b1 заготовок типу А, b2 – типу В, b3 – типу С. При цьому можна розкроїти трьома способами. Кількість заготовок кожного листа за кожним способом розкрою зазначено в таблиці. Скільки листів потрібно розкроювати кожним способом розкрою?
8. Для виробництва трьох видів товарів Т1, Т2, Т3 використовується три типи ресурсів Р1, Р2, Р3. Кількість одиниць кожного ресурсу, для виробництва кожного товару, а також запаси кожного ресурсу подано в таблиці. Знайти кількість товарів кожного виду, які можна виробити за умови використання всього запасу ресурсів.
9. З пункту А в пункт В треба перевезти обладнання 3-х типів: В1 – b1 од., B2 − b2 од., B3 − b3 од. на трьох видах транспорту. Кількість обладнання кожного типу, яке можна розмістити в одиниці певного транспорту, наведено в таблиці. Скільки треба транспортних одиниць кожного виду для перевезення всього обладнання?
10. Підприємство складається з трьох цехів, у кожному з яких виробляють відповідний (один) вид продукції. У кожному цеху на потреби виробництва використовують продукцію всіх цехів цього підприємства (
11. Установлено, що витрати W(x) на обробку митних документів різних призначень Dk у кількості відповідно хk задовольняють закономірності
12. З деякого листового матеріалу треба розкроїти b1 заготовок типу А, b2 – типу В, b3 – типу С. При цьому можна розкроїти трьома способами. Кількість заготовок кожного листа за кожним способом розкрою зазначено в таблиці. Скільки листів потрібно розкроювати кожним способом розкрою?
13. Для виробництва трьох видів товарів Т1, Т2, Т3 використовується три типи ресурсів Р1, Р2, Р3. Кількість одиниць кожного ресурсу, для виробництва кожного товару, а також запаси кожного ресурсу подано в таблиці. Знайти кількість товарів кожного виду, які можна виробити за умови використання всього запасу ресурсів.
14. З пункту А в пункт В треба перевезти обладнання 3-х типів: В1 – b1 од., B2 − b2 од., B3 − b3 од. на трьох видах транспорту. Кількість обладнання кожного типу, яке можна розмістити в одиниці певного транспорту, наведено в таблиці. Скільки треба транспортних одиниць кожного виду для перевезення всього обладнання?
15. Підприємство складається з трьох цехів, у кожному з яких виробляють відповідний (один) вид продукції. У кожному цеху на потреби виробництва використовують продукцію всіх цехів цього підприємства (
16. Установлено, що витрати W(x) на обробку митних документів різних призначень Dk у кількості відповідно хk задовольняють закономірності
17. З деякого листового матеріалу треба розкроїти b1 заготовок типу А, b2 – типу В, b3 – типу С. При цьому можна розкроїти трьома способами. Кількість заготовок кожного листа за кожним способом розкрою зазначено в таблиці. Скільки листів потрібно розкроювати кожним способом розкрою?
18. Для виробництва трьох видів товарів Т1, Т2, Т3 використовується три типи ресурсів Р1, Р2, Р3. Кількість одиниць кожного ресурсу, для виробництва кожного товару, а також запаси кожного ресурсу подано в таблиці. Знайти кількість товарів кожного виду, які можна виробити за умови використання всього запасу ресурсів.
19. З пункту А в пункт В треба перевезти обладнання 3-х типів: В1 – b1 од., B2 − b2 од., B3 − b3 од. на трьох видах транспорту. Кількість обладнання кожного типу, яке можна розмістити в одиниці певного транспорту, наведено в таблиці. Скільки треба транспортних одиниць кожного виду для перевезення всього обладнання?
20. Підприємство складається з трьох цехів, у кожному з яких виробляють відповідний (один) вид продукції. У кожному цеху на потреби виробництва використовують продукцію всіх цехів цього підприємства (
Поиск по сайту: |
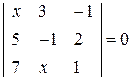 . 2.
. 2.  . 3.
. 3.  .
.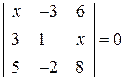 . 5.
. 5. 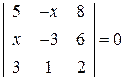 . 6.
. 6. 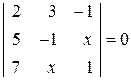 .
.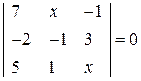 . 8.
. 8.  . 9.
. 9. 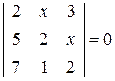 .
. . 11.
. 11.  . 12.
. 12.  .
. . 14.
. 14. 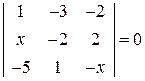 . 15.
. 15.  .
.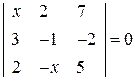 . 17.
. 17.  . 18.
. 18.  .
. . 20.
. 20. 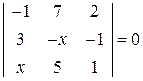 . 21.
. 21. 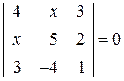 .
.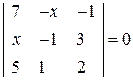 . 23.
. 23. 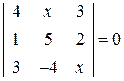 . 24.
. 24. 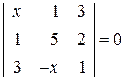 .
.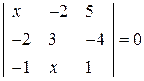 . 26.
. 26.  . 27.
. 27.  .
.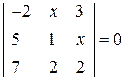 . 29.
. 29.  . 30.
. 30.  .
. . 2.
. 2. 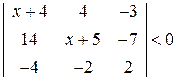 .
.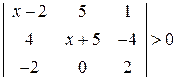 . 4.
. 4. 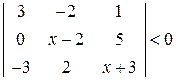 .
.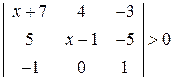 . 6.
. 6. 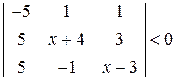 .
. . 8.
. 8. 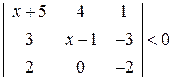 .
. . 10.
. 10. 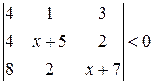 .
. . 12.
. 12. 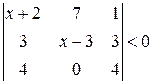
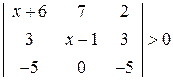 . 14.
. 14. 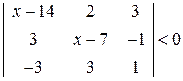 .
.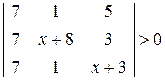 . 16.
. 16. 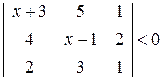 .
. . 18.
. 18. 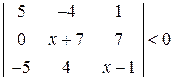 .
. . 20.
. 20.  .
. . 22.
. 22. 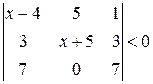 .
.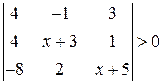 . 24.
. 24.  .
.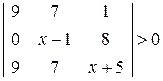 . 26.
. 26.  .
. . 28.
. 28.  .
. . 30.
. 30. 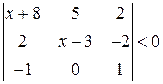 .
.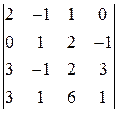 . 2.
. 2.  . 3.
. 3.  .
. . 5.
. 5.  . 6.
. 6. 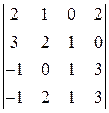 .
. . 8.
. 8. 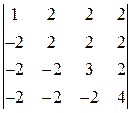 . 9.
. 9.  .
.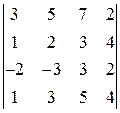 . 11.
. 11. 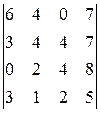 . 12.
. 12.  .
. . 14.
. 14.  . 15.
. 15.  .
. . 17.
. 17. 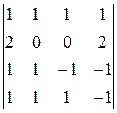 . 18.
. 18. 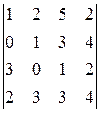 .
.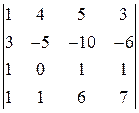 . 21.
. 21. 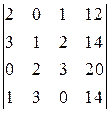 . 23.
. 23.  . 24.
. 24. 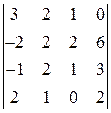 .
.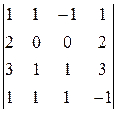 . 26.
. 26. 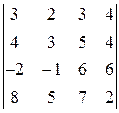 . 27.
. 27.  .
. . 29.
. 29.  . 30.
. 30.  .
. ;
;  ;
;  ;
;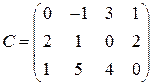 .
.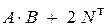 . 2.
. 2.  .
. . 4.
. 4.  .
. . 6.
. 6. 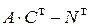 .
. . 8.
. 8. 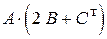 .
. . 10.
. 10. 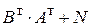 .
.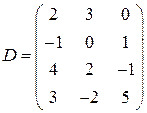 ;
; 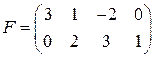 ;
; 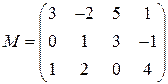 .
. . 12.
. 12.  .
. . 14.
. 14.  .
. . 16.
. 16.  .
. . 18.
. 18.  .
.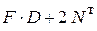 . 20.
. 20.  .
. ;
;  ;
;  .
. . 22.
. 22.  .
. . 24.
. 24. 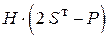 .
. . 26.
. 26.  .
. . 28.
. 28. 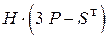 .
.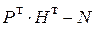 .
.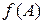 від матриці А, якщо
від матриці А, якщо  і матриця А дорівнює:
і матриця А дорівнює: ; 2.
; 2. 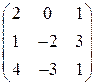 ; 3.
; 3. 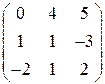 ;
; ; 5.
; 5.  ; 6.
; 6.  ;
; ; 8.
; 8.  ; 9.
; 9.  ;
;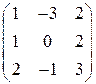 11.
11. 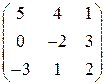 ; 12.
; 12. 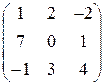 ;
; ; 14.
; 14.  ; 15.
; 15. 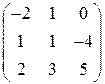 ;
; ; 17.
; 17.  ; 18.
; 18. 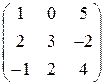 ;
;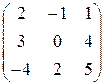 ; 20.
; 20. 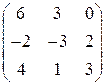 ; 21.
; 21.  ;
;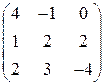 ; 23.
; 23. 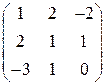 ; 24.
; 24. 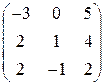 ;
; ; 26.
; 26.  ; 27.
; 27. 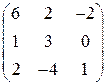 ;
; ; 29.
; 29.  ; 30.
; 30. 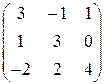 .
.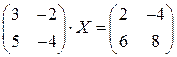 ; 2.
; 2. 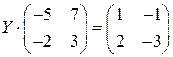 ;
;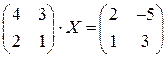 ; 4.
; 4. 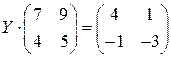 ;
;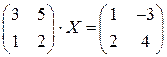 ; 6.
; 6.  ;
; ; 8.
; 8. 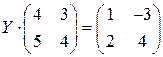 ;
;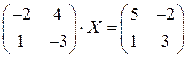 ; 10.
; 10. 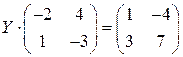 ;
;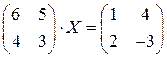 ; 12.
; 12.  ;
;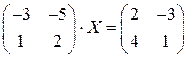 ; 14.
; 14.  ;
; ; 16.
; 16.  ;
; ; 18.
; 18.  ;
; ; 20.
; 20. 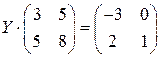 ;
; ; 22.
; 22. 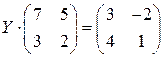 ;
; ; 24.
; 24. 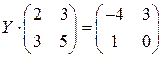 ;
; ; 26.
; 26. 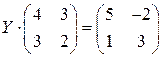 ;
; ; 28.
; 28. 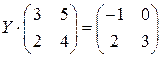 ;
; ; 30.
; 30.  .
. . 2.
. 2.  .
.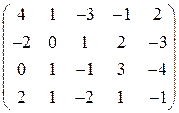 . 4.
. 4.  .
. . 6.
. 6. 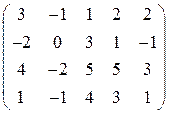 .
.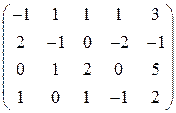 . 8.
. 8.  .
.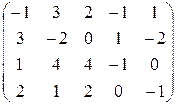 . 10.
. 10. 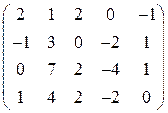 .
. . 12.
. 12. 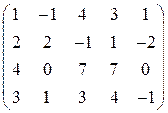 .
. . 14.
. 14. 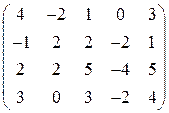 .
. . 16.
. 16. 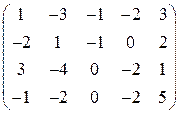 .
. . 18.
. 18. 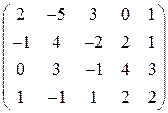 .
.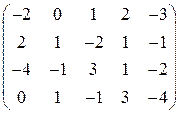 . 20.
. 20.  .
. . 22.
. 22.  .
.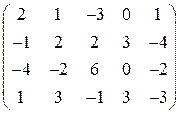 . 24.
. 24. 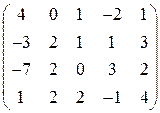 .
.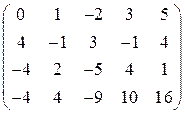 . 26.
. 26.  .
. . 28.
. 28.  .
.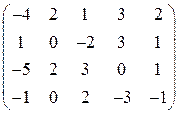 . 30.
. 30.  .
. відповідно у кількості
відповідно у кількості 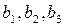 . Для цього потрібні матеріали
. Для цього потрібні матеріали  і трудові ресурси
і трудові ресурси 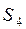 . Кількість кожного виду матеріалу і трудових ресурсів, потрібних на кожний тип приміщень, виражена в деяких умовних одиницях і подається матрицею.
. Кількість кожного виду матеріалу і трудових ресурсів, потрібних на кожний тип приміщень, виражена в деяких умовних одиницях і подається матрицею. ,
, показує скільки одиниць ресурсу
показує скільки одиниць ресурсу 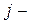 го типу витрачається на одне приміщення i − го типу. Одиниця матеріалів
го типу витрачається на одне приміщення i − го типу. Одиниця матеріалів 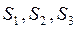 коштує відповідно
коштує відповідно 
 , а одиниця робочої сили
, а одиниця робочої сили  Отже, маємо ще дві матриці:
Отже, маємо ще дві матриці:  і
і 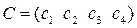 .
. ; 2. А =
; 2. А =  ; 3. А =
; 3. А =  ;
;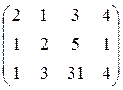 ; 5. А =
; 5. А = 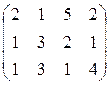 ; 6. А =
; 6. А =  ;
; ; 8. А =
; 8. А = 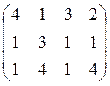 ; 9. А =
; 9. А = 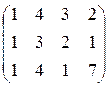 ;
; ; 11. А =
; 11. А =  ; 12. А =
; 12. А = 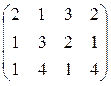 ;
; 15. А =
15. А =  ;
; ; 18. А=
; 18. А= 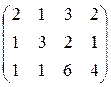 .
. ; 21. А =
; 21. А = 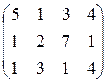 ; 23. А =
; 23. А =  ; 24. А =
; 24. А =  ;
;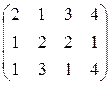 ; 26. А =
; 26. А =  ; 27. А =
; 27. А = 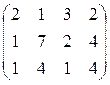 ;
; ;
; використовується чотири види ресурсів
використовується чотири види ресурсів 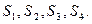 Кількість одиниць кожного ресурсу для виробництва одиниці кожного виробу дається матрицею
Кількість одиниць кожного ресурсу для виробництва одиниці кожного виробу дається матрицею ,
, показує, скільки одиниць сировини
показує, скільки одиниць сировини  го типу витрачається на одиницю продукції i − го типу. План випуску продукції подається матрицею-рядком
го типу витрачається на одиницю продукції i − го типу. План випуску продукції подається матрицею-рядком 
 − кількість виробів типу
− кількість виробів типу 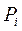 .
. Знайти:
Знайти: ; 2.
; 2.  ; 3.
; 3.  ;
;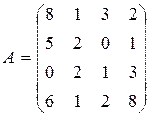 ; 6.
; 6.  ;
;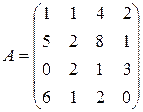 ; 8.
; 8. 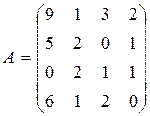 ; 9.
; 9. 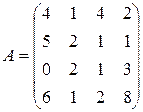 ;
;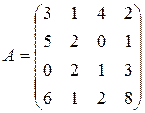 ; 11.
; 11.  ; 12.
; 12. 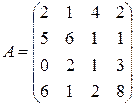 ;
;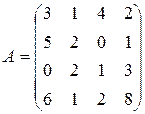 ; 14.
; 14. 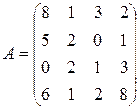 ; 15.
; 15.  ;
;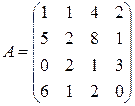 ; 17.
; 17.  ; 18.
; 18. 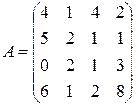 ;
; ; 20.
; 20. 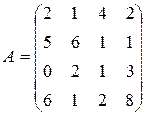 ;
;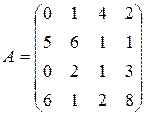 .
. ;
;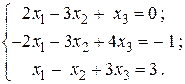 2.
2. 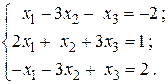
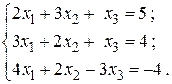 4.
4. 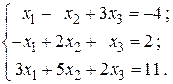
 6.
6. 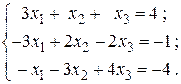
 8.
8. 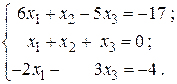
 10.
10. 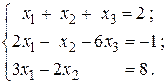
 12.
12. 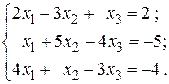
 14.
14. 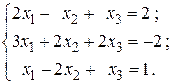
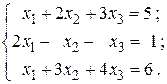 16.
16. 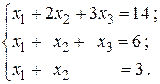
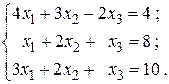 18.
18. 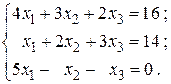
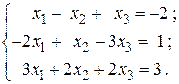 20.
20. 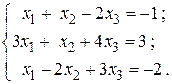
 22.
22. 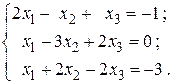
 24.
24. 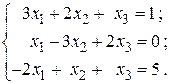
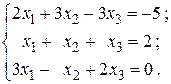 26.
26. 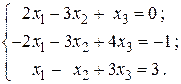
 28.
28. 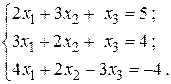
 30.
30. 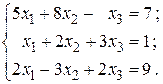
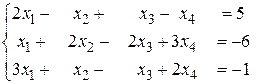 б)
б) 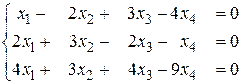
 б)
б) 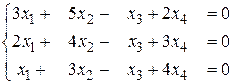
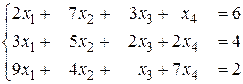 б)
б) 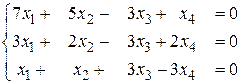
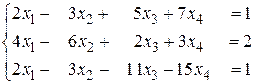 б)
б) 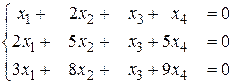
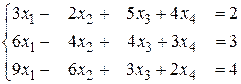 б)
б) 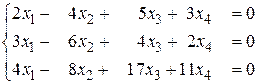
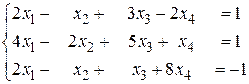 б)
б) 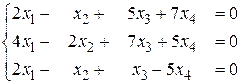
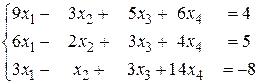 б)
б) 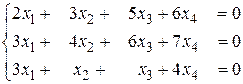
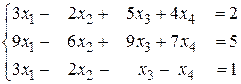 б)
б) 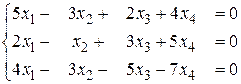
 б)
б) 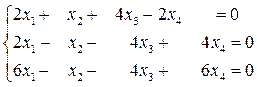
 б)
б) 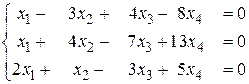
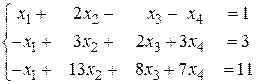 б)
б) 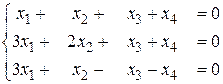
 б)
б) 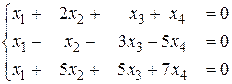
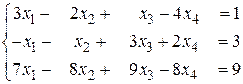 б)
б) 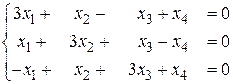
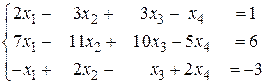 б)
б) 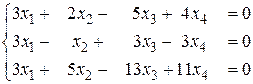
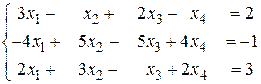 б)
б) 
 б)
б) 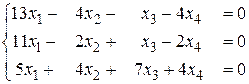
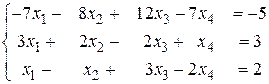 б)
б) 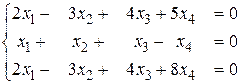
 б)
б) 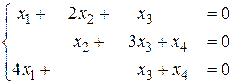
 б)
б) 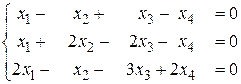
 б)
б) 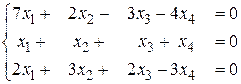
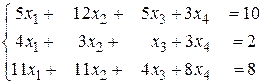 б)
б) 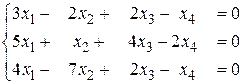
 б)
б) 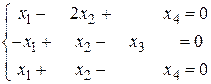
 б)
б) 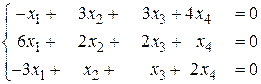
 б)
б) 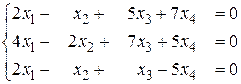
 б)
б) 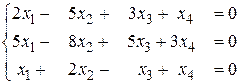
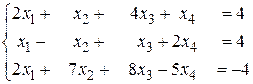 б)
б) 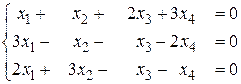
 б)
б) 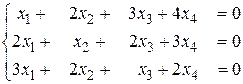
 б)
б) 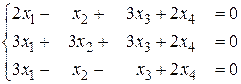
 б)
б) 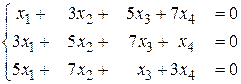
 б)
б) 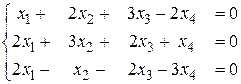
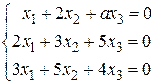 2.
2. 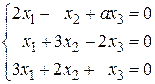
 4.
4. 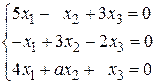
 6.
6. 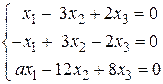
 8.
8. 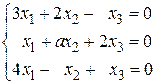
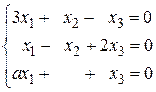 10.
10. 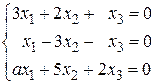
 12.
12. 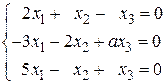
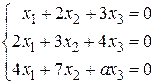 14.
14. 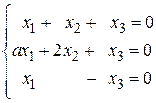
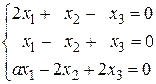 16.
16. 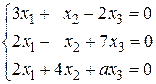
 18.
18. 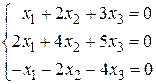
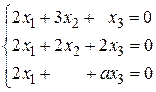 20.
20. 
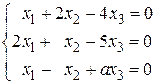 22.
22. 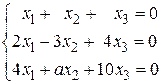
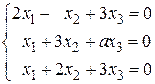 24.
24. 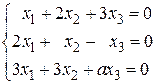
 26.
26. 
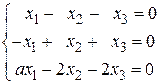 28.
28. 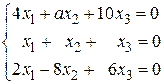
 30.
30. 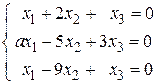
 . У таблиці в умовних одиницях надано середні витрати на кожний к−ий тип документів. Визначити коефіцієнти ak і записати функцію W(x).
. У таблиці в умовних одиницях надано середні витрати на кожний к−ий тип документів. Визначити коефіцієнти ak і записати функцію W(x).
 ТК
Рі
ТК
Рі
 − кількість одиниць продукції і−го цеху, які використовують для виготовлення одиниці продукції j−го цеху). Відомі технологічна матриця
− кількість одиниць продукції і−го цеху, які використовують для виготовлення одиниці продукції j−го цеху). Відомі технологічна матриця  і обсяги В продукції підприємства, замовленої для продажу на ринку. Визначити вектор Х обсягів виробництва для кожного цеху.
і обсяги В продукції підприємства, замовленої для продажу на ринку. Визначити вектор Х обсягів виробництва для кожного цеху.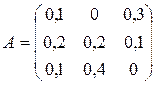 ;
;  .
. ТК
Рі
ТК
Рі
 ;
; 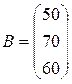 .
.
 ТК
Рі
ТК
Рі
 ;
; 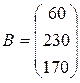 .
.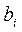
 ТК
Рі
ТК
Рі