 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Уточнення коренів нелінійних рівнянь
Розглянемо уточнення кореня методом ділення навпіл. Ідея методу полягає в тому, що за один його крок вузький проміжок вдається звузити вдвоє. Для цього достатньо проаналізувати знаки функції Припустимо, що на вузькому проміжку [а,Ь] знаходиться єдиний корінь рівняння При формулюванні алгоритму пошуку кореня нам буде зручно користуватись функцією „знак х” , яка визначається наступним чином:
Алгоритм уточнення:
Знайдене значення кореня доцільно перевірити. Для цього його треба підставити у задане рівняння і обчислити значення функції. Якщо значення функції виявилось близьким до нуля, то значення кореня можна вважати вірним.
3.1.Протабулювати функцію 3.2.Відокремити корені нелінійного рівняння графічним та аналітичним способом (табличним), тобто вказати проміжки, на яких точно є корені. 3.3. Уточнити корені нелінійних рівнянь (методом ділення навпіл). Варіанти: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30) Завдання №4. Знаходження розв’язку системи лінійних алгебраїчних рівнянь. Система m лінійних рівнянь з n невідомими має вигляд:
де
Систему лінійних рівнянь можна записати у матричному вигляді, як
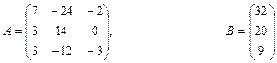
Якщо виконується умова При розв’язуванні системи лінійних рівнянь можливі три випадки: a) m<n. При m<n, якщо система m лінійних рівнянь з n невідомими є сумісною, то вона не визначена і має нескінченну кількість розв’язків. b) m=n. При m=n, система (1) буде мати n лінійних рівнянь з n невідомими. Тоді розв’язок системи можна отримати методом оберненої матриці чи методом Крамера. Метод оберненої матриці розв’язування системи лінійних рівнянь. Помножимо ліву і праву частину (2) на обернену матрицю Після необхідних перетворень розв`язок лінійної системи методом оберненої матриці матиме вигляд
Метод Крамера розв’язування системи лінійних рівнянь. Цей метод базується на формулах Xi=|∆i|/|A| , (4) де |∆i| - визначник матриці , одержаної з матриці А заміною і –го стовпця на стовпець вільних членів В; |A| - визначник матриці А. c) m>n. У випадку, якщо m>n і система є сумісною, то матриця А має принаймні m-n лінійно незалежних рядків. Тут розв’язок може бути отримано добором n будь-яких лінійно незалежних рівнянь і застосуванням формули (3). Однак із застосуванням комп'ютера зручніше використовувати більш загальний підхід – метод найменших квадратів. Для цього обидві частини матричного рівняння системи (2) множимо ліворуч на транспоновану матрицю системи АТ АТАХ=АТ В Потім обидві частини рівняння множимо ліворуч на матрицю (АТА)-1 . Якщо ця матриця існує,то система визначена. З врахуванням того, що (АТА)-1 *(АТА)=Е , одержуємо Х=(АТА)-1 *АТВ (5) Матричне рівняння (5) є розв’язком системи m лінійних рівнянь з n невідомими при m>n. 4.1.Розв’язати систему лінійних алгебраїчних рівнянь 4.2. Порівняти результати. Варіанти: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30) Завдання №5. Наближення функції, заданих таблично, методом найменших квадратів. Значення аргумента і функції задані в таблиці. а) використовуючи метод найменших квадратів, побудувати апроксимаційний поліном першого степеня б) побудувати графіки функції заданої таблично і знайденого методом найменших квадратів апроксимаційного полінома першого степеня
Варіанти: 1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
21)
22)
23)
24)
25)
26)
27)
28)
29)
30)
Поиск по сайту: |
на лівому кінці відрізка і в його середині. Різні знаки є свідченням того, що шуканий корень знаходиться саме на ньому, і тому праву половину відрізка можна відкинути. У протилежному випадку можна відкинути ліву половину відрізка.
. Треба знайти його значення із заданою точністю ε . Це означає, що шуканий корінь знаходиться у проміжку, ширина якого не перевищує ε, і тоді значенням кореня можна вважати середину цього проміжка.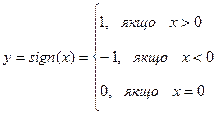
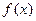в точці а, тобто 
.
.
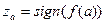, то вважати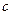 
коренем рівняння 
.
, то вважати 
.
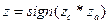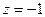, то значення b замінити на значення 
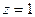, то значення a замінити на значення 
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
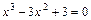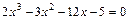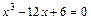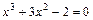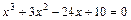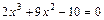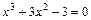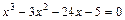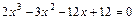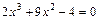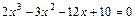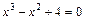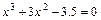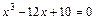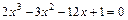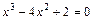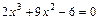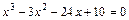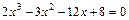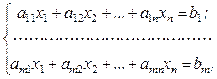(1)
- матриця коефіцієнтів при змінних (матриця системи);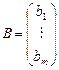
- матриця-стовпець (вектор) вільних членів;
- матриця-стовпець (вектор) невідомих.
(2)
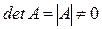, то система має один розв`язок.
, тоді 
, де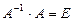 
(одинична матриця).
(3)
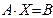вище перерахованими методами.
;
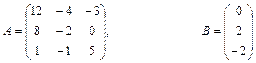
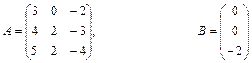
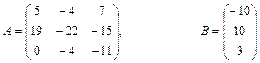
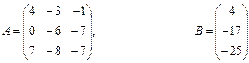
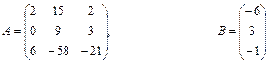
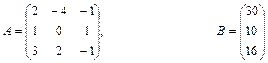
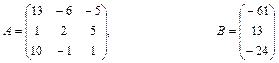
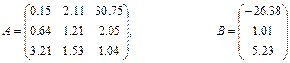
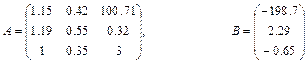
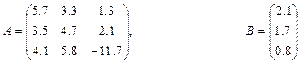
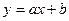