 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Завдання №1. Табуляція функціїСтр 1 из 5Следующая ⇒
Рівне - 2012 Методичні поради та завдання для розрахункової роботи №1 з курсу ,,Комп’ютерні технології та програмування“ для студентів заочної форми навчання за напрямком підготовки 6.050202 “Автоматизація та комп’ютерно-інтегровані технології” (А.П. Сафоник - Рівне: НУВГП, 2012. – 38с.)
Розробник: А.П. Сафоник, кандидат техн. наук, доцент кафедри автоматизації та комп’ютерно-інтегрованих технологій НУВГП.
Відповідальний за випуск - зав. кафедри автоматизації та комп’ютерно-інтегрованих технологій, професор, академік УЕАН Б.О. Баховець
Затверджено на засіданні кафедри автоматизації та комп’ютерно-інтегрованих технологій
Протокол № _7_ від “_29_”_листопада_2012 р.
Зав. кафедри _______________________Б.О. Баховець
Рекомендовано методичною комісією за напрямом підготовки 6.050202 „Автоматизація та комп’ютерно-інтегровані технології”
Протокол № _4_ від “_29_”_листопада_2012 р.
Голова ____________________________ Б.О. Баховець
ББК 32.973 Ó А.П. Сафоник, 2012 Ó НУВГП, 2012 І. МЕТА ВИКОНАННЯ РОЗРАХУНКОВО-ГРАФІЧНОЇ РОБОТИ Для того щоб навчитись використовувати теоретичні знання при організації обчислювальних робіт на комп’ютері, методика вивчення курсу передбачає виконання розрахунково-графічної роботи, завдання якої, охоплюють найважливіші елементи з обробки даних засобами табличного процесора. Розрахунково-графічна робота складається із п’яти завдань і передбачає закріплення, перевірку та поглиблення знань, набутих студентом в результаті вивчення Модуля ІІІ курсу. В результаті виконання розрахунково-графічної роботи, студент навчиться: - представляти у математичному вигляді, умову поставленої задачі; - будувати оптимальний алгоритм, який приведе до розв’язку; - працювати з формулами табличного процесора; - робити аналіз отриманих результатів; ІІ. ЗАВДАННЯ НА РОЗРАХУНКОВО-ГРАФІЧНУ РОБОТУ Завдання на розрахунково-графічну роботу є індивідуальним для кожного студента групи, і обирається згідно вказівок, наведених нижче. Варіанти для кожного завдання студент визначає за двома останніми цифрами номера залікової книжки (шифру) за допомогою таблиці вибору варіантів завдань розрахунково-графічної роботи. Згідно із варіантами в даній таблиці, у кожному завданні студент вибирає конкретні пункти завдань з додаткових таблиць варіантів кожного завдання. Наприклад, якщо номер варіанта завдання контрольної роботи 77, то завдання слід виконувати таким чином: завдання 1 – пункт 07; завдання 2 – пункт 16; завдання 3 – пункт 25; завдання 4 – пункт 04; завдання 5 – пункт 13; Кожне із завдань передбачає побудову відповідної електронної таблиці, яка формується в ТП Excel і зберігається на диску у формі закінченого модуля в окремій книзі з відповідною назвою (наприклад: zavd1.xls, zavd2.xls, zavd3.xls, zavd4.xls, zavd5.xls). Якщо завдання передбачає використання декількох листів робочої книги, то їм (листам) потрібно дати унікальні імена. Таблиця вибору варіантів розрахунково-графічної роботи.
Завдання №1. Табуляція функції 1.1. За заданими дійсними числами a,b (b>a) і цілому Отримані результати
1.2. Побудувати графік кожної функції в окремій системі координат; 1.3. На одній системі координат побудувати графік всіх функцій.
Варіанти:
В кожному варіанті вказані номери функції 1) 2) 3) 4) 5) 6) 7) 8) 9) 10)
Завдання №2. Обчислення інтегралів. Обчислити значення означеного інтегралу Формули чисельного інтегрування: а) „правих” прямокутників:
б)„лівих” прямокутників:
в)„центральних” прямокутників
г)трапецій:
д)Симпсона:
у формулах чисельного інтегрування позначено: n – число елементарних відрізків, на які поділяється проміжок інтегрування Варіанти:
Завдання №3. Знаходження коренів нелінійних рівнянь. Задано нелінійне рівняння
Поиск по сайту: |
 обчислити значення функцій
обчислити значення функцій  для значень аргументу
для значень аргументу  , де
, де  .
.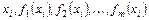 надрукувати у вигляді таблиці:
надрукувати у вигляді таблиці:











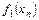




















 вибираються із наступного списку:
вибираються із наступного списку: 11)
11)  21)
21) 
 12)
12)  22)
22) 
 13)
13)  23)
23) 
 14)
14)  24)
24) 
 15)
15)  25)
25) 
 16)
16)  26)
26) 
 17)
17)  27)
27) 
 18)
18)  28)
28) 
 19)
19)  29)
29) 
 20)
20)  30)
30) 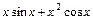
 ,розбивши проміжок
,розбивши проміжок 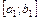 на
на  рівних частин за формулою
рівних частин за формулою 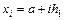 , де
, де  змінюється в межах
змінюється в межах  , а крок розбиття проміжку
, а крок розбиття проміжку  . Побудувати графік функції
. Побудувати графік функції  .
.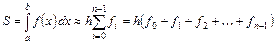


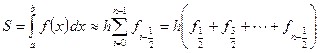


 ; h – крок інтегрування
; h – крок інтегрування  ;
;  ;
;  - середня точка елементарного відрізка
- середня точка елементарного відрізка  ;
;  - значення підінтегральної функції відповідно в точках
- значення підінтегральної функції відповідно в точках  ; значення функцій
; значення функцій  ,
,  ,
,  .
.






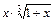

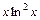
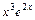

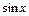





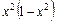





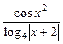



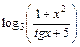



 .
.