 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вопрос 3. Мода и медиана, их смысл и значение в социально-экономических исследованиях, способы вычисления ⇐ ПредыдущаяСтр 2 из 2
Из структурных средних, характеризующих особенности распределения частот внутри ранжированных и вариационных рядов, получили распространение мода, медиана, средние величины. Модой в статистике называется величина признака (варианта), которая наиболее часто встречается в данной совокупности. В вариационном ряду это будет варианта, имеющая наибольшую частоту. В дискретном вариационном ряду модой называют ту варианту, которая имеет наибольшую частоту повторения. В интервальном ряду моду определяют по формуле: М0=х0+i∙ где х0- нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту); i– величина модального интервала; fМо – частота модального интервала; fМо-1 – частота интервала, предшествующего модальному; fМо+1 - частота интервала, следующего за модальным. ПРИМЕР 4. Распределение предприятий по численности промышленно-производственного персонала характеризуется следующими данными, приведенными таблице.
По формуле (2.11) рассчитаем моду:
В интервальном ряду с неравными интервалами применяется плотность распределения (частное от деления частоты на величину принятого интервала).
Медианой в статистике называется значение признака у единицы, которая расположена в середине упорядоченного ряда, а в вариационном ряду медианой будет величина признака, которая делит ряд пополам по сумме накопленных частот. По данным интервального вариационного ряда медиана определяется по следующей формуле:
где
Вначале определяется медианный интервал по сумме накопленных частот, превышающих половину всех значений частот. ПРИМЕР 4. Для данных примера 4 медианным интервалом будет 400–500. Рассчитаем медиану
Для характеристики структуры применяются квартили, которые делят ранжированную совокупность по сумме накопленных частот на четыре равные части. Различают квартиль нижний (Q1), отделяющий 1/4 часть совокупности с наименьшими значениями признака и квартиль верхний (Q4),отсекающий 1/4 часть с наибольшими значениями признака.
Поиск по сайту: |
 (2.11);
(2.11); =400,
=400,  =30,
=30,  =7,
=7,  =19,
=19,  =100.
=100.
 чел.
чел. (2.12)
(2.12) - начало медианного интервала;
- начало медианного интервала;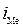 - величина медианного интервала;
- величина медианного интервала; - сумма накопленных частот до медианного интервала;
- сумма накопленных частот до медианного интервала; - частота медианного интервала.
- частота медианного интервала. .
.