 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вопрос 2. Средняя арифметическая, ее основные математические свойства и методы расчетаСтр 1 из 2Следующая ⇒
Тема 1.6. Средние величины Вопрос 1. Сущность и значение средних величин. Вопрос 2. Средняя арифметическая, ее основные математические свойства и методы расчета. Вопрос 3. Мода и медиана, их смысл и значение в социально-экономических исследованиях, способы вычисления. Вопрос 1. Сущность и значение средних величин. Задача средних величин – охарактеризовать все единицы статистической совокупности одним значением признака. Средняя величина – это обобщающая характеристика единиц совокупности по какому–либо варьирующему признаку. Средние величины позволяют сравнивать уровни одного и того же признака в различных совокупностях и находить причины этих расхождений. Средние величины являются обобщающими показателями, в которых находят выражение действие общих условий, закономерность изучаемого явления. Статистические средние величины рассчитываются на основе массовых данных статистически правильно организованного массового наблюдения. Если статистическая средняя рассчитывается по массовым данным для качественно однородной совокупности (массовых явлений), то она будет объективной. Средняя величина абстрактна, так как характеризует значение абстрактной единицы.От разнообразия признака у отдельных объектов абстрагируется средняя. Абстракция – ступень научного исследования. В средней величине осуществляется диалектическое единство отдельного и общего. Средние величины должны применяться исходя из диалектического понимания категорий индивидуального и общего, единичного и массового. Средняя отображает что–то общее, которое складывается в определенном единичном объекте. Для выявления закономерностей в массовых общественных процессах средняя величина имеет большое значение. В средней величине отражается характерный, типичный, реальный уровень изучаемых явлений. Задачей средних величин является характеристика этих уровней и их изменений во времени и пространстве.
Средний показатель – это обычное значение, потому что формируется в нормальных, естественных, общих условиях существования конкретного массового явления, рассматриваемого в целом.
Вопрос 2. Средняя арифметическая, ее основные математические свойства и методы расчета. Так как статистическая размерность различна, то приходится применять в расчетах различные виды средних: - арифметическую, - гармоническую, - геометрическую, - квадратическую и другие, относящиеся к роду степенных средних. Для расчета простых степенных средних применяется формула:
Взвешенные средние рассчитываются по формуле:
где
m – показатель степени средней; n – число единиц;
Для первичных признаков применяются простые средние, для вторичных – взвешенные. Один из наиболее распространенных видов средней – средняя арифметическая, которая исчисляется тогда, когда объем осредняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности (при этом m = 1). Для вычисления средней арифметической величины сумму всех уровней признака делят на их число.
Средняя арифметическая взвешенная применяется в расчетах, когда индивидуальные значения определяемого признака имеют различную частоту повторения:
Когда отдельные варианты представлены в виде интервалов «от и до», в качестве варианта принимается середина интервалов. При наличии открытых интервалов границы их устанавливаются условно, исходя из конкретных условий задачи, или с учетом предыдущего интервала.
ПРИМЕР 2. Объем производства и себестоимость единицы продукции А по трем заводам характеризуются следующими данными.
Исчислить среднюю себестоимость по трем заводам:
Средняя гармоническая применяется, когда индивидуальные значения выражены в форме обратных показателей. Если вес каждого варианта равен единице, то при n вариантах формула средней гармонической имеет вид
Формула средней гармонической взвешенной следующая:
ПРИМЕР 2. Издержки производства и себестоимость единицы продукции А по трем заводам характеризуются следующими данными.
Исчислить среднюю себестоимость по трем заводам:
Средняя геометрическая применяется для расчетов средних темпов за определенный период, т. е. тогда, когда определяющий показатель (величина, определяющая вид средней) является не суммой значений, а их произведением:
Средняя квадратическая применяется в тех случаях, когда приходится осреднять величины в виде квадратных функций (например, при расчетах диаметра труб, стволов); в статистике используется как мера вариации. Рассчитывается по формулам:
Как было отмечено, применение той или иной средней величины зависит от сущности явления и исходной информации. Между средними существует следующее соотношение, названное правилом мажорантности средних:
Поиск по сайту: |
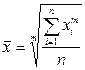 . (2.1)
. (2.1) , (2.2)
, (2.2) – индивидуальные значения осредняемых признаков, варианты;
– индивидуальные значения осредняемых признаков, варианты; – среднее значение исследуемого явления;
– среднее значение исследуемого явления; – вес, частота.
– вес, частота. . (2.3)
. (2.3)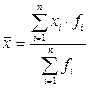 . (2.4)
. (2.4) = 22 тыс. руб.
= 22 тыс. руб. . (2.5)
. (2.5) . (2.6)
. (2.6)

 (простая); (2.7)
(простая); (2.7) (взвешенная). (2.8)
(взвешенная). (2.8) (простая); (2.9)
(простая); (2.9) (взвешенная). (2.10)
(взвешенная). (2.10)