 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Утворення різьби та види різьб
Якщо на циліндр діаметром d2 (рис. 5.2) навивати прямокутний трикутник так, щоб один із катетів збігався з основою циліндра, то гіпотенуза трикутника утворить на циліндрі гвинтову лінію. Кут y називається кутом підйому гвинтової лінії, а р – кроком різьби. З рис. 5.2 випливає
Якщо по гвинтовій лінії переміщати яку-небудь фігуру (трикутник, трапецію і т. п.) так, щоб фігура лежала в площині, що проходить через вісь циліндра, фігура опише тіло, що називається різьбою. Розташовані між канавками виступи називають витками різьби. Під витком різьби прийнято розуміти ту частину її, що охоплює різьбову деталь у межах до 360°. Виступ різьби, що охоплює різьбову деталь більше одного разу, тобто більше ніж 360°, називають ниткою різьби. По профілю поперечного перетину різьби розрізняють: 1) трикутну (рис. 5.3, а), що одержала найбільше застосування, – для кріпильних і інших деталей. Трикутні різьби бувають метричні (із кутом профілю a=60°) і дюймові (a=55°). При проектуванні нових машин застосовують тільки метричну різьбу, дюймова застосовується для заміни різьбових деталей старих і імпортних машин, а також у деяких особливих випадках (наприклад, як кріпильно-ущільнювальна для з'єднань водо- і газопровідних труб і арматури); 2) трапецеїдальну (рис. 5.3, б), що застосовується в ходових гвинтах верстатів, гвинтах супортів, вантажних гвинтах; служить основною різьбою для передач гвинт-гайка. Зручна для виготовлення й у порівнянні з трикутною різьбою має менші втрати на тертя, а в порівнянні з прямокутною – більш міцна. Трапецеїдальна різьба має кут профілю a=30°. Вона стандартизована в діапазоні діаметрів від 8 до 640 мм; 3) упорну (рис. 5.3, в), що застосовується в механізмах з односторонньо направленим зусиллям, наприклад, у пресах, гвинтових домкратах, вантажних гаках і т.п. Має несиметричний трапецеїдальний профіль витків. Кут нахилу робочої сторони профілю для підвищення ККД обраний досить малим – 3° (різьба з кутом нахилу профілю 0° незручна у виготовленні), кут нахилу неробочої сторони профілю 30°; 4) прямокутну (рис. 5.3, г), область застосування якої та ж, що і для трапецеїдальної і упорної різьби. Прямокутна різьба виготовляється на токарно-гвинторізних верстатах. Такий спосіб не дозволяє одержати високу точність (при куті нахилу профілю 0° утруднене застосування більш точних методів обробки). Тому ця різьба застосовується порівняно рідко і не стандартизована; 5) круглу (рис. 5.3, д), що застосовується для гвинтів, що зазнають дії великих динамічних навантажень і працюють у забрудненому середовищі з частим відкручуванням і загвинчуванням (вагонні зчіпки, пожежна арматура). Застосовується також у тонкостінних деталях (цоколі і патрони електричних ламп, протигази и т.п.). Окремі види круглої різьби стандартизовані.
Різьба, нарізана на зовнішній поверхні стержня, називається зовнішньою, нарізана на внутрішній поверхні отвору – внутрішньою. У залежності від форми стержня або отвору, на яких нарізана різьба, розрізняють різьби циліндричні і конічні. Найбільше поширення одержали циліндричні різьби як самі прості і зручні при виготовленні і зборці. За напрямком гвинтової лінії розрізняють праву і ліву різьби. У правої різьби гвинтова лінія йде зліва направо і нагору, у лівої – справа наліво і нагору. Найбільше поширена права різьба, ліву різьбу застосовують тільки в спеціальних випадках. У залежності від кількості ниток різьби, із яких вона утворена, розрізняють однозахідну, двозахідну і т. д. різьби. У різьбових з'єднаннях застосовують переважно однозахідні різьби як більш надійні щодо самовідгвинчування. Всі кріпильні різьби однозахідні. Багатозахідні різьби застосовуються переважно в гвинтових механізмах. Число заходів більше трьох застосовується рідко.
Різьби виготовляють нарізуванням (вручну, на токарно-гвинторізних верстатах або на спеціальних верстатах, фрезеруванням); накатуванням; литтям; видавлюванням. Нарізка вручну робиться мітчиками або плашками. Цей спосіб малопродуктивний, його застосовують в індивідуальному виробництві і при ремонтних роботах. Найбільш продуктивним і дешевим способом виготовлення стандартних кріпильних деталей є накатка на спеціальних різьбонакатних верстатах-автоматах. Накатка істотно зміцнює різьбові деталі. Геометричні параметри різьби (рис. 5.4): d – зовнішній діаметр; d1 – внутрішній діаметр (номінальні значення d та d1 однакові для гвинта і гайки, зазори в западинах утворюються за рахунок граничних відхилень розмірів діаметрів); d2– середній діаметр; h – робоча висота профілю, по якій стикаються бічні сторони різьб гвинта і гайки; р – крок (відстань між однойменними сторонами сусідніх профілів, вимірювана в напрямку осі різьби); р1 – хід (поступальне переміщення твірного профілю за один оберт або відносне переміщення гайки за один оберт). Для однозахідної різьби р1=р; для багатозахідної р1=пр, де п – число заходів різьби; a – кут профілю; y – кут підйому (див. рис. 5.2). Для багатозахідних різьб 5.3. Класифікація різьбових з‘єднань У залежності від характеру навантаження і способу зборки деталей різьбові з'єднання підрозділяються на напружені і ненапружені. Різьбове з'єднання буде ненапруженим, якщо напруження в матеріалі різьбових деталей виникають тільки під дією навантаження (наприклад, вантажний гвинт редуктора). У тих випадках, коли напруження в деталях виникають до навантаження, з'єднання буде напруженим. Ці напруження обумовлюються попередньою затяжкою з'єднання (наприклад, кріплення кришки редуктора). У залежності від призначення розрізняють з'єднання міцні (вантажний гвинт редуктора) і міцнощільні (кріплення кришки посудини, що знаходиться під тиском, до корпусу). 5.4. Силові співвідношення, умови самогальмування і ККД Силові співвідношення вивчимо на прикладі прямокутної різьби. Розглянемо гайку (рис. 5.5, а), що нагвинчується на гвинт рушійною силою Ft, прикладеною по середньому колу різьби, i навантажену осьовою силою. Приймемо умову, що все навантаження, прикладене до гайки, зосереджене в точці. Рух гайки можна представити як переміщення вантажу нагору по похилій площині з кутом підйому y, рівним куту підйому різьби гвинта (рис. 5.5, б). Крім сил Ft і Fa на вантаж діють нормальна реакція площини Fn і сила тертя Ff :
Рис. 5.5. Розрахункова схема до визначення силових співвідношень у гвинтовій парі Проектуючи діючі сили на осі x та y, отримуємо (використовуючи умову рівноваги тіла на похилій поверхні)
Розв‘язуючи систему рівнянь (5.3), маємо:
Отримали силу, яку треба прикласти до вантажу, щоб він рухався угору. Відомо, що
Добуток рушійної сили
При відгвинчуванні гайки, тобто при опусканні вантажу по похилій площині вниз, аналогічно можна отримати:
Із виразу (5.8) виходить, що: 1) якщо 2) якщо 3) якщо Таким чином, умовою спокою вантажу на похилій площині, тобто умовою самогальмування різьби буде:
Коефіцієнт корисної дії визначається відношенням роботи сил корисного опору При підйомі вантажу по похилій площині рушійною силою Коефіцієнт корисної дії гвинтової пари з прямокутною різьбою при нагвинчуванні гайки:
Підставляючи у рівняння (5.10) р із (5.1) і
Визначимо сили тертя й установимо співвідношення між силами тертя в прямокутній і трикутній різьбах.
Сила тертя для прямокутної різьби (рис. 5.6, а) Сила тертя для трикутної різьби (рис. 5.6, б)
Отримане співвідношення справедливе і для трапецеїдальної різьби. Співвідношенню коефіцієнтів тертя
Співвідношення між силами в прямокутній і трикутній різьбах аналогічні. Тому за аналогією з формулами (5.6), (5.7) і (5.9) випливає, що для трикутної (трапецеїдальної, упорної) різьби окружна сила
крутний момент у різьбі
умова самогальмування
коефіцієнт корисної дії
Визначимо момент тертя
де Момент тертя на торці гайки або головки гвинта
Для спрощення розрахунків приймають, що рівнодійна сила тертя
Таким чином, момент загвинчування гайки чи гвинта
5.5. Розрахунок різьбових з‘єднань
Болти і гвинти виходять із ладу як правило через розрив стержня по різьбі або по перехідному перетину біля головки, руйнування або ушкодження різьби, руйнування головки. Оскільки розміри стандартних болтів відповідають умові їх рівноміцності, розрахунок звичайно роблять по одному основному критерію працездатності – міцності нарізаної частини стержня. Розглянемо характерні випадки статичного навантаження з‘єднання. 5.5.1. З'єднання, навантажене осьовою розтяжною силою, попередня і кінцева затяжка його відсутні. Характерним прикладом такого навантаження може служити різьбовий кінець вантажного гака (рис. 5.8). Стержень працює на розтяг. Рівняння міцності:
де Із рівняння (5.20) отримаємо:
або
Отримане по рівнянню (5.21) значення внутрішнього діаметра різьби округляють за стандартом до найближчого більшого значення У відповідальних з'єднаннях витки різьби перевіряються на згин, зріз і зминання (питомий тиск). Представимо розгорнутий виток різьби, як консольну балку. Вважаючи, що навантаження між витками різьби гайки розподіляється рівномірно, навантаження на один виток буде дорівнювати
Умова міцності витка різьби на згин:
Умова міцності витка різьби на зріз:
При перевірці міцності різьби за питомим тиском допускається, що навантаження розподіляється рівномірно на проекцію витка різьби на горизонтальну площину:
Рівняння (5.22) – (5.24) застосовуються при перевірочному розрахунку витків різьби. Розв‘язуючи праву частину кожного з названих рівнянь відносно
Із отриманих трьох значень Встановлено, що навантаження між витками різьби гайки розподіляється нерівномірно. Так, відповідно до розрахунків М.Є. Жуковського перший виток різьби гайки сприймає 34% навантаження, другий – 22%, третій – 10% і т. д. Десятий виток різьби гайки сприймає менше 1% діючого зусилля. У зв'язку з цим гайки недоцільно виготовляти з більшим числом витків різьби ( 5.5.2. Болт сприймає розтяг і кручення. Такі умови навантаження виникають, якщо після навантаження болта робочим зусиллям
Рис. 5.10. Схема гвинтової стяжки Під дією осьової сили в матеріалі гвинта виникають напруження розтягу:
Під дією моменту гвинтової пари Тоді
Розділивши (5.29) на (5.28) із врахуванням, що для стандартних сталевих болтів із метричною різьбою Еквівалентне напруження в матеріалі болта від сили
З рівняння (5.30) випливає, що при підтягуванні різьбового з'єднання, навантаженого осьовою силою, у матеріалі деталей напруження зростають на 30%. Для компенсації цього перенапруження розрахунок роблять по розрахунковому навантаженню
5.5.3. Попередньо затягнутий болт, додатково навантажений осьовою розтяжною силою; можливе наступне затягування болта. Цей вид навантавження найпоширеніший, тому що для більшості різьбових з'єднань потрібне попереднє затягування болтів, що забезпечує щільність з'єднання і відсутність взаємних зсувів деталей стику, що порушують роботу з'єднання. Прикладом таких з'єднань можуть служити болти для кріплення кришок посудин, що знаходяться під великим тиском, болти для кріплення фланців редукторів, фундаментні болти і т. п. У результаті попереднього затягування болта силою
Рис. 5.11. Розрахункова схема до визначення розмірів різьби попередньо напруженого різьбового з‘єднання Задача про розподіл сили Після прикладення зовнішнього навантаження до моменту розкриття стику болт додатково розтягнеться на деяку величину
Із рівняння (5.32) коефіцієнт зовнішнього навантаження дорівнює:
При великій податливості болта Затягування болта повинне забезпечити герметичність з'єднання або нерозкриття стику під навантаженням. Зусилля нерозкриття стику:
З викладеного випливає, що розтягуюча сила, що діє на болт після попереднього затягування і прикладення зовнішньої сили (рис. 5.11, б)
При відсутності наступного затягування болт розраховують з врахуванням обертаючого моменту попереднього затягування по розрахунковій силі
При обчисленні по формулах (5.35) і (5.36) сил Проектний розрахунок болта при відсутності наступного затягування виконують по формулі
Проектний розрахунок болта, для якого можливе наступне затягування, роблять з врахуванням обертаючого моменту, викликаного цим затягуванням, по розрахунковій силі, рівній 1,3
5.5.4. Болт навантажений поперечною силою, встановлений у отвір з зазором. У випадку установки болта в отвір із зазором (рис. 5.12) його необхідно затягти такою силою По отриманій розрахунковій силі визначають внутрішній діаметр різьби болта:
або
Для зменшення діаметра болта застосовують різні пристрої, що розвантажують болт від сприйняття поперечних сил (наприклад, розвантажувальну втулку, шпонку, штифт і т. п.). У цьому випадку розраховується на міцність деталь, що сприймає поперечне навантаження, а діаметр болта приймається конструктивно.
5.5.5. Болт, навантажений поперечною силою, встановлений у отвір з-під розвертки без зазора. При постановці болта без зазора (рис. 5.13) з'єднання збирається без попереднього затягування. Поперечне навантаження Умова міцності на зріз:
Формулою (5.40) користуються при перевірочному розрахунку болта. Проектний розрахунок виконується по формулі або
Умова міцності на зминання:
5.5.6. Попередньо затягнутий болт з ексцентричною головкою додатково навантажений зовнішньою силою
де
де а – ексцентриситет навантаження. Приймаючи
або З приведених рівнянь випливає, що при такому навантаженні максимальні напруження в матеріалі болта різко зростають (при Ексцентричне навантаження діє і на болт із симетричною головкою, якщо опорні поверхні мають перекіс. Для виключення такого явища поверхні з'єднуваних деталей під головкою болта і гайкою обробляють. Клемові з'єднання Клемові з'єднання застосовуються для закріплення на валах і інших круглих стержнях різних деталей (кривошипів, важелів і т.п.) при необхідності подальших перестановок. По конструкції розрізняють два основних типи клемових з'єднань: а) із ступицею, що має проріз (рис. 5.15); б) із роз‘ємною ступицею (рис. 5.16).
У клемових з'єднаннях використовують сили тертя, що виникають від затягування болтів і дозволяють навантажувати з'єднання як моментом ( До переваг клемового з'єднання відносяться простота монтажу, самозапобігання від перевантаження, а також можливість перестановки і регулювання взаємного розташування деталей як в осьовому, так і окруж-
ному напрямках. При цьому вал не послабляється шпонковою канавкою. Недоліком є ненадійність передачі навантаження силами тертя і дисбаланс насаджених на вал деталей. Тому клемові з'єднання не застосовуються для передачі великих навантажень, а також при великих швидкостях обертання. У залежності від конструкції з'єднання при розрахунку можна розглянути два граничних випадки (див. рис. 5.16). Перший випадок. Клема має велику жорсткість, а посадка виконана з великим зазором (рис. 5.16, а). При цьому можна припустити, що контакт деталей відбувається по лінії. Запишемо відповідно умови міцності при навантаженні з'єднання моментом
де За умовою рівноваги половини клеми Підставляючи значення
Другий випадок. Клема досить гнучка, форма деталей, що стикуються, строго циліндрична, зазор у з'єднанні близький до нуля (рис. 5.16). При такій конструкції можна прийняти, що тиск р розподілений рівномірно по поверхні стику деталей. У цьому випадку умови міцності з'єднання при навантаженні моментом Т або осьовою силою
Із умови рівноваги клеми
Підставляючи значення р (5.48) у рівняння (5.47), знаходимо:
Із зіставлення рівнянь (5.48) і (5.49) випливає, що навантажувальні спроможності клемового з'єднання для двох цих граничних випадків відносяться, як У сучасному машинобудуванні розміри деталей клемового з'єднання виконують під посадку, при якій забезпечується вільна зборка деталей без зайвих зазорів. Це дає підставу розглядати умови роботи практично виконуваних клемових з'єднань як середні між двома розглянутими крайніми випадками і розраховувати їх на міцність по формулах
де 2,5 і 5 – коефіцієнти, приблизно рівні середньому значенню коефіцієнтів у формулах (5.46) і (5.49). Розрахунок клемового з‘єднання з одностороннім розташуванням болтів (див. рис. 5.15) прийнято також виконувати по формулах (5.50). при цьому умовно вважають, що функції другого болта з‘єднання виконує сам матеріал важеля. Використовуючи формули (5.50), визначимо потрібну силу затяжки болта
при дії осьової сили
де k – коефіцієнт запасу(k = 1,3…1,8); z – число болтів, розташованих по один бік вала. При спільній дії Т і
Після визначення сили
6. КЛИНОВІ ТА ШТИФТОВІ З‘ЄДНАННЯ 6.1. Клинові з‘єднання Клиновими називають роз‘ємні з'єднання, здійснювані за допомогою клина. За призначенням розрізняють клинові з'єднання: силові (служать для міцного з'єднання деталей машин) і установочні (призначені для регулювання й установки деталей машин у потрібному положенні). Прикладом міцного клинового з'єднання служить з'єднання за допомогою клина 2 штока 1 із стержнем 3 (рис. 6.1).
У залежності від методу зборки розрізняють клинові з'єднання ненапружені (що збираються без попереднього затягування) і напружені (що збираються з попереднім затягуванням). Ненапружені з'єднання призначаються для сприйняття постійних за знаком зусиль (рис. 6.1). При знакозмінних динамічних навантаженнях застосовуються напружені конструкції (рис. 6.2), в яких до прикладення зовнішнього навантаження при запресуванні клина створюється попереднє затягування. Обов'язкова умова надійної роботи таких з'єднань – зберігання залишкового затягування деталей після прикладення зовнішнього навантаження. Конструктивно напруженість клинового з'єднання досягається за допомогою бурта стержня (див. рис. 6.2), посадкою хвостовика стержня у
втулці на конус, упором торця хвостовика в дно отвору втулки. Застосовувані в клинових з'єднаннях клини бувають односкосі, двоскосі і безскосі (безскосий клин називають чекою). У силових клинових з'єднаннях застосовують, як правило, односкосі клини. У силовому клиновому з'єднанні клин установлюють на робоче місце забиванням (іноді затягуванням за допомогою гвинта). Клин утримується здебільшого лише тертям. Для надійності самогальмування клинів необхідно, щоб дотримувалася умова Переваги клинових з'єднань: 1) простота конструкції; 2) зручність і простота зборки і розбирання; 3) забезпечення центрування з‘єднуваних деталей; 4) можливість передавати великі навантаження. Недоліки клинових з‘єднань: 1) нетехнологічність конструкції (складність обробки деталей з‘єднання); 2) ослаблення з'єднуваних деталей прорізами для установки клина; 3) необхідність застосування у відповідальних випадках пристроїв, що стопорять клин. Перераховані недоліки обмежують область застосування клинових з'єднань, у даний час застосовуваних там, де зручність і швидкість зборки і розбирання мають вирішальне значення (наприклад, у парових машинах, двигунах внутрішнього згоряння, у затискних пристроях станочних пристроїв і т. п.). При розрахунку ненапружених клинових з'єднань за розрахункове приймається найбільше зовнішнє навантаження, прикладене до з'єднання. Стержень працює на розтяг. Умова міцності в перерізі А-А (рис. 6.3):
Рис 6.3. Розрахункова схема до визначення розмірів стержня клинового з‘єднання Товщина клина приймається
Напруження зминання під клином:
Розмір
Умова міцності на зминання опорної поверхні у втулці (рис. 6.4):
Рис. 6.4. Розрахункова схема до визначення розмірів втулки і штока клинового з‘єднання Міцність втулки на розтяг перевіряється за умовою
Розмір
Як правило приймають Аналіз випадків руйнування клина показує, що до початку процесу зрізання клин піддається деформації згину. Тому висоту середнього перерізу клина h визначають з умови міцності на згин (рис. 6.5). Клин розглядається як балка, що лежить на двох опорах із рівномірно розподіленим навантаженням із боку стержня. Тоді згинаючий момент:
Рис. 6.5. Розрахункова схема до визначення розмірів клина Момент опору
звідки
Вважаючи
Довжину клина зазвичай приймають
Штифтові з'єднання Штифти призначаються для точного взаємного фіксування деталей (кришки відносно корпуса редуктора, рис. 6.6, а) і для передачі невеликих навантажень (кріплення зубчастого колеса на валі, рис. 6.6, б). По конструкції штифти бувають конічні (рис. 6.7, а) і циліндричні (рис. 6.7, б), гладкі і просічні (рис. 6.7, в), тобто з насіченими або видавленими канавками.
Рис. 6.7. Види штифтів Циліндричні гладкі штифти ставляться в отвір із натягом і утримуються від випадання тертям або за допомогою спеціальних пристроїв. Недолік циліндричних штифтів – ослаблення посадки при повторних розбираннях і зборках. Конічні штифти виконуються з конусністю 1:50, що забезпечує надійність самогальмування і центрування деталей. Конічні штифти можуть бути поставлені в той саме отвір кілька разів. Просічні штифти застосовуються тільки для скріплення деталей машин. У порівнянні з гладкими вони не вимагають розгортки отворів і більш надійні від випадання. Ці штифти допускають багатократну зборку і розбирання з'єднань. Штифти виготовляють із сталі Ст 4, Ст 5, Сталь 35, Сталь 40, Сталь 45. Просічні штифти рекомендується виготовляти із пружинної сталі (Сталь 65Г). Діаметр установочних штифтів приймають конструктивно; діаметр кріпильного штифта визначають із розрахунку штифта на зріз. При дії на штифт сили F, перпендикулярної до його осі, умова міцності на зріз при z площинах зрізу:
де
Поиск по сайту: |
 Рис. 5.2. Схема утворення різьби
Рис. 5.2. Схема утворення різьби
 . (5.1)
. (5.1) Рис. 5.3. Види різьб
Рис. 5.3. Види різьб Рис. 5.4. Геометричні параметри різьби
Рис. 5.4. Геометричні параметри різьби
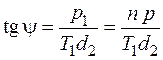 . Всі геометричні параметри різьб і допуски на їхні розміри стандартизовані.
. Всі геометричні параметри різьб і допуски на їхні розміри стандартизовані. , (5.2)
, (5.2)
 (5.3)
(5.3) ,
,  . (5.4)
. (5.4) , (5.5)
, (5.5) . (5.6)
. (5.6) на середній радіус дає момент у гвинтовій парі:
на середній радіус дає момент у гвинтовій парі: . (5.7)
. (5.7) . (5.8)
. (5.8)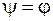 , то
, то  , тобто вантаж буде знаходитись у стані спокою;
, тобто вантаж буде знаходитись у стані спокою; , то
, то  , тобто вантаж буде знаходитись у стані спокою на площині і для його руху необхідно прикласти якесь додаткове навантаження;
, тобто вантаж буде знаходитись у стані спокою на площині і для його руху необхідно прикласти якесь додаткове навантаження; , то
, то  , тобто вантаж буде рухатись вниз під дією своєї ваги без дії додаткової сили.
, тобто вантаж буде рухатись вниз під дією своєї ваги без дії додаткової сили.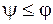 . (5.9)
. (5.9) до роботи рушійних сил
до роботи рушійних сил  .
.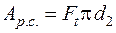 , а робота сил корисного опору
, а робота сил корисного опору  .
. . (5.10)
. (5.10) . (5.11)
. (5.11) Рис. 5.6. Розрахункова схема до визначення співвідношень сил, що діють у прямокутній (а) і трикутній (б) різьбах
Рис. 5.6. Розрахункова схема до визначення співвідношень сил, що діють у прямокутній (а) і трикутній (б) різьбах
 , де f – коефіцієнт тертя.
, де f – коефіцієнт тертя. , де a – кут профілю різьби;
, де a – кут профілю різьби; 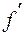 – приведений коефіцієнт тертя;
– приведений коефіцієнт тертя; . (5.12)
. (5.12) і
і 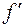 відповідає співвідношення між кутами тертя
відповідає співвідношення між кутами тертя  і
і  , де
, де  .
.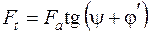 ; (5.13)
; (5.13) ; (5.14)
; (5.14) ; (5.15)
; (5.15) . (5.16)
. (5.16) Рис. 5.7. Розрахункова схема до визначення моменту сил тертя на торці головки гайки (гвинта)
Рис. 5.7. Розрахункова схема до визначення моменту сил тертя на торці головки гайки (гвинта)
 на торці гайки або головки гвинта (рис. 5.7) при їхньому загвинчуванні. Питомий тиск на опорній поверхні
на торці гайки або головки гвинта (рис. 5.7) при їхньому загвинчуванні. Питомий тиск на опорній поверхні ,
,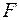 – сила притиснення гайки або головки гвинта.
– сила притиснення гайки або головки гвинта. , звідки
, звідки
 . (5.17)
. (5.17) на опорній поверхні гайки або головки гвинта діє по дотичній до кола середнього діаметра
на опорній поверхні гайки або головки гвинта діє по дотичній до кола середнього діаметра  опорної поверхні. Тоді момент
опорної поверхні. Тоді момент , (5.18)
, (5.18) .
. . (5.19)
. (5.19) Рис. 5.8. Кріплення
вантажного гака
Рис. 5.8. Кріплення
вантажного гака
 , (5.20)
, (5.20) – розрахункове напруження розтягу в поперечному перетині нарізаної частини стержня;
– розрахункове напруження розтягу в поперечному перетині нарізаної частини стержня;  – внутрішній діаметр різьби;
– внутрішній діаметр різьби;  – допустиме напруження на розтяг матеріалу стержня.
– допустиме напруження на розтяг матеріалу стержня. ,
, . (5.21)
. (5.21)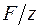 , де
, де  – число витків різьби гайки (рис. 5.9).
– число витків різьби гайки (рис. 5.9). Рис. 5.9. Розрахункова схема до перевірки різьби
Рис. 5.9. Розрахункова схема до перевірки різьби
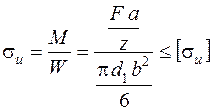 . (5.22)
. (5.22) . (5.23)
. (5.23) . (5.24)
. (5.24) ; (5.25)
; (5.25) ; (5.26)
; (5.26) . (5.27)
. (5.27) ).
).
 . (5.28)
. (5.28) виникають напруження кручення
виникають напруження кручення  , де
, де  – момент опору при крученні;
– момент опору при крученні;  – момент у гвинтовій парі.
– момент у гвинтовій парі. . (5.29)
. (5.29) = 2°30¢,
= 2°30¢,  = 1,12 і
= 1,12 і  0,5.
0,5. . (5.30)
. (5.30)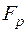 , що перевищує на 30% задане, тобто
, що перевищує на 30% задане, тобто  . Таким чином, проектний розрахунок болта в цьому випадку варто робити по формулі
. Таким чином, проектний розрахунок болта в цьому випадку варто робити по формулі 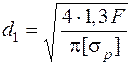 або
або . (5.31)
. (5.31) болт розтягується, а деталі стику стискаються. Після прикладення зовнішнього навантаження (рис. 5.11, а) тільки частина його
болт розтягується, а деталі стику стискаються. Після прикладення зовнішнього навантаження (рис. 5.11, а) тільки частина його  додатково навантажує болт, а інша частина
додатково навантажує болт, а інша частина  йде на часткове розвантаження деталей стику від стиску (рис. 5.11, б). Коефіцієнт
йде на часткове розвантаження деталей стику від стиску (рис. 5.11, б). Коефіцієнт  , що враховує долю зовнішнього навантаження
, що враховує долю зовнішнього навантаження 
 , а деформація деталей зменшиться на ту ж величину, тобто
, а деформація деталей зменшиться на ту ж величину, тобто , (5.32)
, (5.32)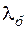 – податливість болта, рівна його деформації при одиничному навантаженні;
– податливість болта, рівна його деформації при одиничному навантаженні;  – сумарна податливість з'єднуваних болтом деталей .
– сумарна податливість з'єднуваних болтом деталей . . (5.33)
. (5.33) , (5.34)
, (5.34) – коефіцієнт затяжки болта, що враховує силу попередньої затяжки болта
– коефіцієнт затяжки болта, що враховує силу попередньої затяжки болта  , або
, або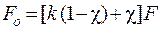 . (5.35)
. (5.35) , або
, або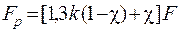 . (5.36)
. (5.36) і
і  , звідки
, звідки . (5.37)
. (5.37) , звідки
, звідки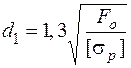 . (5.38)
. (5.38) Рис. 5.12 Різьбове з‘єднання, навантажене поперечною силою (болт встановлений у отвір з зазором)
Рис. 5.12 Різьбове з‘єднання, навантажене поперечною силою (болт встановлений у отвір з зазором)
 була більше поперечної сили
була більше поперечної сили  (1,2 – коефіцієнт запасу). Тоді необхідна сила стиску деталей (затягування болта)
(1,2 – коефіцієнт запасу). Тоді необхідна сила стиску деталей (затягування болта)  , де
, де  .
.
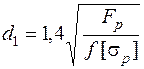 . (5.39)
. (5.39) Рис. 5.13.
Рис. 5.13.
 ).
).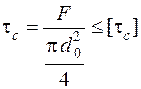 , (5.40)
, (5.40)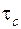 – розрахункове напруження зрізу болта;
– розрахункове напруження зрізу болта;  – діаметр стержня болта в небезпечному перерізі; [
– діаметр стержня болта в небезпечному перерізі; [ 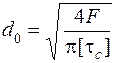
 . (5.41)
. (5.41) , (5.42)
, (5.42) – розрахункове напруження зминання в з'єднанні;
– розрахункове напруження зминання в з'єднанні; 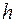 – довжина частини болта, яка піддається найбільшому зминанню; [
– довжина частини болта, яка піддається найбільшому зминанню; [  ,
,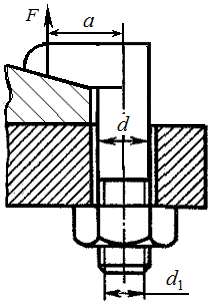 Рис. 5.14
Рис. 5.14
 – найбільше сумарне напруження болта від розтягу і згину;
– найбільше сумарне напруження болта від розтягу і згину;  – розрахункове напруження відповідно на розтяг і згин.
– розрахункове напруження відповідно на розтяг і згин. , (5.43)
, (5.43) , отримуємо
, отримуємо ,
, . (5.44)
. (5.44)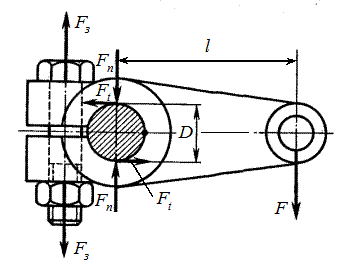 Рис. 5.15. Клемове з‘єднання
(ступиця деталі має прорізь)
Рис. 5.15. Клемове з‘єднання
(ступиця деталі має прорізь)
 ) (рис. 5.15), так і осьовою силою
) (рис. 5.15), так і осьовою силою  .
. Рис. 5.16. Клемове з‘єднання (ступиця деталі роз‘ємна)
Рис. 5.16. Клемове з‘єднання (ступиця деталі роз‘ємна) або осьовою силою
або осьовою силою  або
або  , (5.45)
, (5.45) – сила тертя (
– сила тертя (  );
);  – реакція в зоні контакту ;
– реакція в зоні контакту ;  , де
, де 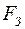 – сила затягування болтів.
– сила затягування болтів. у формули (5.45), отримаємо
у формули (5.45), отримаємо . (5.46)
. (5.46)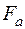 відповідно мають вигляд:
відповідно мають вигляд: (5.47)
(5.47) отримаємо:
отримаємо: . (5.48)
. (5.48)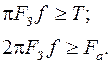 (5.49)
(5.49) . Тому з умови необхідного затягування болтів перший випадок самий несприятливий, а другий найбільш сприятливий (потрібна найменша сила затягування болтів). Крім того, наявність великих зазорів у з'єднанні може привести до руйнування клеми від напруження згину. Практично конструкції з великими зазорами недосконалі і не застосовуються.
. Тому з умови необхідного затягування болтів перший випадок самий несприятливий, а другий найбільш сприятливий (потрібна найменша сила затягування болтів). Крім того, наявність великих зазорів у з'єднанні може привести до руйнування клеми від напруження згину. Практично конструкції з великими зазорами недосконалі і не застосовуються.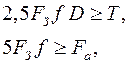 (5.50)
(5.50) . При дії момента Т
. При дії момента Т ; (5.51)
; (5.51) , (5.52)
, (5.52) сил
сил
 . (5.53)
. (5.53) . (5.54)
. (5.54) Рис. 6.1. Ненапружене клинове з‘єднання
Рис. 6.1. Ненапружене клинове з‘єднання
 Рис. 6.2. Напружене клинове з‘єднання
Рис. 6.2. Напружене клинове з‘єднання
 , де a – кут клина, а j – кут тертя. З цією метою ухил
, де a – кут клина, а j – кут тертя. З цією метою ухил  у силових клинових з'єднаннях звичайно приймають рівним 1:100, 1:40 або 1:30. Установочні клини виконують з ухилами 1:10, 1:6, 1:4; в усіх випадках при i>1:25 необхідні пристрої, що забезпечують невипадання клину, тобто при і<1:25 і безударних навантаженнях такі пристрої не потрібні, оскільки забезпечується самогальмування. Кріпильні клини звичайно виконують із сталі Ст 4, Ст 5, сталь 35, сталь 40, сталь 45.
у силових клинових з'єднаннях звичайно приймають рівним 1:100, 1:40 або 1:30. Установочні клини виконують з ухилами 1:10, 1:6, 1:4; в усіх випадках при i>1:25 необхідні пристрої, що забезпечують невипадання клину, тобто при і<1:25 і безударних навантаженнях такі пристрої не потрібні, оскільки забезпечується самогальмування. Кріпильні клини звичайно виконують із сталі Ст 4, Ст 5, сталь 35, сталь 40, сталь 45.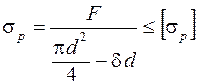 . (6.1)
. (6.1)
 ; при
; при  із (6.1) визначимо d:
із (6.1) визначимо d: . (6.2)
. (6.2) . (6.3)
. (6.3) визначається із умови міцності на зріз:
визначається із умови міцності на зріз: (6.4)
(6.4) , (6.5)
, (6.5) .
.
 . (6.6)
. (6.6) може бути знайдений із умови міцності втулки на зріз
може бути знайдений із умови міцності втулки на зріз (6.7)
(6.7) , де h – висота клина в середньому перерізі. Діаметр втулки приймають
, де h – висота клина в середньому перерізі. Діаметр втулки приймають 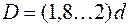 .
.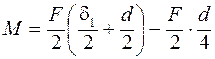 .
.
 . Умова міцності на згин:
. Умова міцності на згин: , (6.8)
, (6.8) . (6.9)
. (6.9) і
і  , отримаємо
, отримаємо . (6.10)
. (6.10)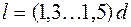 ; матеріал клинів Ст 5, Ст 6 та ін. При розрахунку напружених клинових з‘єднань з урахуванням напружень від попередньої затяжки розрахункове навантаження збільшують на 25%. Тоді:
; матеріал клинів Ст 5, Ст 6 та ін. При розрахунку напружених клинових з‘єднань з урахуванням напружень від попередньої затяжки розрахункове навантаження збільшують на 25%. Тоді: . (6.11)
. (6.11) Рис. 6.6. Види штифтових з‘єднань
Рис. 6.6. Види штифтових з‘єднань
 ,
, , (6.12)
, (6.12) – допустиме напруження на зріз матеріалу штифта.
– допустиме напруження на зріз матеріалу штифта.