 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Розвивання в ряд Тейлора ⇐ ПредыдущаяСтр 2 из 2
В задачах апроксимації і наближення функції f(x) важливе значення має розвивання функцій в ряд Тейлора в околі точки а:
Якщо а=0, отримаємо ряд Маклорена: >>taylor(f,n,x,a) в загальному випадку можна задати кількість членів ряда, змінну, по якій шукається розвивання, точку, в околі якої виконується розвивання.
>>taylor(f) повертає 6 членів ряда Маклорена
taylor(f,n) повертає члени ряда Маклорена до (n-1)-го порядка
taylor(f,a) повертає ряд Тейлора в околі точки А ????Як розрізнити – де кількість членів ряда, а де точка?
>>taylor(f,x) повертає ряд Тейлора для змінної х, яка визначається автоматично функцією findsym(f).
Приклади: >> x=sym('x'); >> F=sin(x); >> taylor(F) ans = x-1/6*x^3+1/120*x^5 >> taylor(F,10) ans = x-1/6*x^3+1/120*x^5-1/5040*x^7+1/362880*x^9 >> taylor(exp(x),1) ans = >> taylor(cos(x),-pi/2,6) ans = x+1/2*pi-1/6*(x+1/2*pi)^3+1/120*(x+1/2*pi)^5 Обчислення сум рядів В матаналізі досить часто приходиться обчислювати суми деякої функції f(i) від цілочисленних значень аргумента i від a до b:
>>symsum(S) повертає символьне значення суми нескінченого ряда по змінній, яка шукається автоматично за допомогою функції findsum. >>symsum(S,v) повертає суму нескінченого ряду по змінній v. >>symsum(S,a,b) symsum(S,v,a,b) обчислюються скінчені суми для номерів доданків від а до b. Приклади: >> symsum(x^2) ans = 1/3*x^3-1/2*x^2+1/6*x >> symsum(1/x^4) ans = -1/6*Psi(3,x) >> Psi(3,x) ans = Inf >> symsum(1/x^4,1,5) ans = 14001361/12960000 >> symsum([x,x^2,x^3],1,5) ans = [ 15, 55, 225]
Перетворення виразів >>simplify(S) Спрощує символьний вираз S. Якщо спрощення неможливе, повертає вихідний вираз. >> simple(S) Виконує спрощення з виводом проміжних результатів. >>[r,how]=simple(S) - проміжні результати не виводяться; результат спрощення знаходиться в змінній r, а в how – рядкова змінна, яка вказує на тип перетворення. Приклад: >>syms a b x; >>V=[sin(x)^2+cos(x)^2 log(a*b)] >> simplify(V) Ans= [1 log(a*b)] -------------------------------------------- >>simplify ((a^2-2*a*b+b^2)/(a-b)) Ans= a-b Можливості спрощення виразів в MATLAB скромніші, ніж в Maply у зв’язку з тим, що відсутні опції, за допомогою яких можна задати шлях спрощення.
Приклади: >> [r,how]=simple(cos(x)^2+sin(x)^2) Результат спрощення потрібен для подальшої програмної обробки r = how = Combine -------------------------------------- >> [r,how]=simple(2*cos(x)^2-sin(x)^2) r = 3*cos(x)^2-1 how = Simplify ------------------------------------------- >> [r,how]=simple(cos(x)^2-sin(x)^2) r = cos(2*x) how = Combine ------------------------------------------- >> [r,how]=simple(cos(x)+(-sin(x)^2)^(1/2)) r = cos(x)+i*sin(x) how = radsimp спрощення радікалів ---------------------------------------------- >> [r,how]=simple(cos(x)+i*sin(x)) r = exp(i*x) how = Convert(exp) ---------------------------------------------- >> [r,how]=simple((x+1)*x*(x-1)) r = x^3-x how = Collect(x) ----------------------------------------------- >> [r,how]=simple(x^3+3*x^2+3*x+1) r = (x+1)^3 how = Factor ------------------------------------------------ >> [r,how]=simple(cos(3*acos(x))) r = 4*x^3-3*x how = Expand ------------------------------------------------ >> expand(S) розширює вираз S. Раціональні вирази розкладає на прості дроби, поліноми – на поліноміальні розвивання. Функція працює з багатьма алгебраїчними та тригонометричними функціями. Приклади: >> syms a b x; >> S=[(x+2)*(x+3)*(x+4) sin(2*x)]; >> expand(S) ans = [ x^3+9*x^2+26*x+24, 2*sin(x)*cos(x)] ----------------------------------------- >> expand(sin(a+b)) ans = sin(a)*cos(b)+cos(a)*sin(b) ------------------------------------------- >> expand((a+b)^3) ans = a^3+3*a^2*b+3*a*b^2+b^3 >> factor(S) розкладає вираз на прості множники, цілі числа – на добуток простих чисел. Приклади: >> factor(x^7-1) ans = (x-1)*(x^6+x^5+x^4+x^3+x^2+x+1) >> factor(x^6-1) ans =
(x-1)*(x+1)*(x^2+x+1)*(x^2-x+1) ---------------------------------------- >> factor(x^2-x-1) ans = x^2-x-1 ------------------------------------------- >> factor(123456789) ans = 3 3 3607 3803 Тут ans масив 1*4 ------------------------------------------- >> factor(sym('123456789')) ans = (3)^2*(3803)*(3607) Тут ans sym object 1*1 >> collect(S,x) >> collect(S) Записує вираз по степенях змінної x. Приклади: >> S=[x^3*y^2+x^2*y+3*x*y^2 x^4*y-y*x^2]; >> collect(S,x) ans = [ x^3*y^2+x^2*y+3*x*y^2, x^4*y-x^2*y] ------------------------------------------- >> collect(S,y) ans = [ (x^3+3*x)*y^2+x^2*y, (x^4-x^2)*y] ---------------------------------------------- >> collect(S) ans = [ x^3*y^2+x^2*y+3*x*y^2, x^4*y-x^2*y] >> [N,D]=numdem(S) Перетворює кожен елемент масиву в раціональну форму у вигляді відношення двох неприводимих поліномів з цілочисельнимикоефіцієнтами. N,D – чисельник і знаменник перетвореного елемента масива. Приклади: >> [n,d]=numden(sym(8/10)) n = d = >> [n,d]=numden(x*y+y/x) n = y*(x^2+1) d = x >>horner(P) Перетворює поліном до схеми Горнера. Схема Горнера мінімізує кількість операцій множення. Приклади: >> horner(x^5-2*x^4-3*x^3-2*x^2-5*x-6) ans = -6+(-5+(-2+(-3+(-2+x)*x)*x)*x)*x ------------------------------------------------- >> horner([x^3+x^2+x (x^3+1)*(x^2+2)*(x+3)]) ans = [ (1+(x+1)*x)*x, (x^3+1)*(x^2+2)*(x+3)] ----------------------------------------------------- >> expand((x^3+1)*(x^2+2)*(x+3)) ans = x^6+3*x^5+2*x^4+7*x^3+3*x^2+2*x+6 >> horner(ans) ans = 6+(2+(3+(7+(2+(x+3)*x)*x)*x)*x)*x >>subs(S) Підстановка. Замінює в виразі S всі змінні їх значеннями, які беруться з робочої області MATLAB Якщо повернутися до попереднього прикладу і виконати присвоення значення >>x=1 >>subs(ans) ans=-17
>>subs(S,NEW) замінє в виразі S всі змінні значеннями NEW >>subs(S,OLD,NEW) заміняє в виразі S OLD на NEW. При однакових розмірах масивів OLD NEW заміна виконується поелементно. Приклади: >> syms a b x y; >> subs(x-y,y,1) ans = x-1 --------------------------- >> subs(sin(x)+cos(y),[x,y],[a,b]) ans = sin(a)+cos(b) --------------------------- >> subs(exp(a*x),a,-magic(3)) ans = [ exp(-8*x), exp(-x), exp(-6*x)] [ exp(-3*x), exp(-5*x), exp(-7*x)] [ exp(-4*x), exp(-9*x), exp(-2*x)]
Досить часто виникає необхідність в знаходженні функції, оберненої до заданої. >>g=finverse(f) – повертає функцію, обернену f. Вважається, що мова йде про функцію однієї змінної, наприклад, ‘x’. Тоді g(f(x))=x. >>g=finverse(f,v) повертає функцію, обернену f відносно заданої змінної v, так що g(f(v))=v. Ця форма використовується, якщо f – функція кількох змінних. Приклади: >>finverse(sinh(x)) Ans= Asinh(x) >>finverse(exp(x)) Ans= Log(x)
Поиск по сайту: |
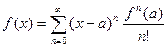
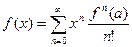
Це скінчена сума. Якщо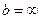 
, говорять про нескінчену суму.