 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Обчислення границь функційСтр 1 из 2Следующая ⇒
Перетворення виразів Точна арифметика MATLAB зазвичай виконує обчислення з числами, поданими в форматі плаваючої крапки з подвійною точністю. Це доволі висока точність, яка задовільняє більшість потреб в прикладних обчислювальних задачах. Однак є задачі, які потребують більш точного результату (задачі теорії чисел). Такі обчислення недуже вдало називають арифметикою довільної точності. Правильно говорити просто про точну арифметику.
Точною арифметикою називають обчислення, у яких всі числа результату є точними. В MATLAB т.а. реалізована в пакеті символьних обчислень. >> digits(D) змінює кількість цифр при обчисленнях в точній арифметиці >> digits Digits=32 повертає кількість цифр за замовчуванням в точній арифметиці Функція format впливає тільки на зображення на екрані!!!
Для того, щоб отримати результат на екрані саме такий, який є в пам'яті комп'ютера, використовують функцію vpa(variable precision arithmetic):
>>vpa(S) повертає результат обчислень змінної S з кількістю цифр, заданих функцією digits.
>>vpa(S,D) повертає результат обчислень змінної S з кількістю цифр, яка задано безпосередньо (D) В точній арифметиці результат зберігається в символьному вигляді. Тип результату sym object (піктограма в робочій області інша). Кількість байт памяті, яку займає символьний об’єкт, залежить від значення digits. Наприклад, якщо функцією digits задається 50 значущих цифр, то в памяті буде 126+2*50 Приклади: >>vpa (exp(1),50) ans=2.718281824590450907955982984276488423347473144531 >>exp(1) ans=2.7183 >> format long >> exp(1) ans = 2.71828182845905 !15 цифр
>>vpa(pi,100) або >>digits(100) >>vpa(pi) Якщо просто >>pi , то буде працювати встановленний за замовчуванням формат. >>vpa(pi, 5000)
>>vpa([2*pi exp(1) log(2)], 10) ans=[6.283185308 2.718281828 .6931471806]
Питання: а чи не можна без функції vpa завжди виконувати обчислення з такою точністю? В принципі можна, але плата за це час і оперативна пам'ять. В математичних виразах можуть використовуватися звичайні змінні таі символьні змінні.
>> a=2; b=4; a,b – звичайні змінні (поняття, відоме з систем програмування), яким присвоєні числові значення. Якщо ввести вираз >> (a-x)*(b-y) (1) Буде виведено повідомлення про помилку ??? Undefined function or variable 'x'. (аналогічно Паскалю – невідома змінна. Але ми збираємося з введеним виразом виконувати не числові, а символьні дії – наприклад, розкрити дужки – перемножити)
>>x=sym(‘x’) створення одного символьного об’єкта >>syms x y створення 2-х символьних об’єктів В ході тривалого сеансу роботи користувач може забути, які змінні символьні. В принципі можна переглянути робочу область. Є спеціальна функція, яка в виразі може виділяти символьні змінні:
findsym(s)– повертає в алфавітному порядку список всіх символьних змінних в виразі s. Якщо таких немає, повертає порожній рядок.
Приклади: >> a=2; b=4; >> findsym(a*x^2+b*y+z)
Якщо раніше була виконана функція >> syms x y z, то буде виведено ans = x, y, z
>> findsym(x+y*i) ans = x, y
Обчислення границь функцій >>limit(F,x,a) обчислює границю функціїї Fза змінноюхв точці а
>>limit(F,x) обчислює границю функціїї F в нулі
>>limit(F,x,a,’right’) >>limit(F,x,a,’left’)
Приклади: >> limit(sin(a*x)/(a*x)) тут ans = >> limit(sin(a*x)/x) тут ans = a >> limit(2*sin(x)/x) ans = >> limit(2+sin(x)/x) ans = аналогічний результат отримаємо, якщо: >> limit(2+sin(x)/x,0) ans = >> limit(tan(x),pi) ans = >> limit(tan(x),pi/2) ans = NaN >> limit(tan(x),x,pi/2,'right') ans = -inf >> limit(tan(x),x,pi/2,'left') ans = inf >> limit([sin(x)/x,(1+x)/(2+x)],x,0) ans = [ 1, 1/2] >>
Обчислення похідних diff(f)знаходить першу похідну функції fза змінною х. . diff(f,n) знаходить похідну n-го порядку функції fза змінною х. . diff(f,n,v)знаходить похідну n-го порядку функції fза змінною v. difff(f,v,n) знаходить похідну n-го порядку функції fза змінною v.
Приклади: >>syms x y; 1)>>diff(x^y) ans= x^y*y/x
2)>> diff(x^y,y) ans = x^y*log(x)
3)>> diff(sin(x*y),3) ans = -y^3*cos(x*y) (перша похідна y*cos(yx) друга похідна –y*y*sin(yx) третя похідна –y*y*y*cos(y*x))
4)>> diff(sin(x*y),3,y) ans = -x^3*cos(x*y)
5)>>diff([x^3 sin(x) exp(x)]) ans= [3*x^2 cos(x) exp(x)] Обчислення інтегралів
int(f) знаходить невизначений інтеграл за змінною х. int(f,v) знаходить невизначений інтеграл за змінною v. int(f,a,b) обчислює визначений інтеграл з межами інтегрування від а до b.Межі інтегрування можуть числовими або символьними змінними. int(f,v,a,b) обчислює визначений інтеграл з межами інтегрування від а до b.
Приклади:
ans= -1/3*sin(x)^2*cos(x)-2/3*cos(x)
ans=log(2*x)*x-x
>> int(sin(2*x)*cos(3*x))
ans =
cos(x)/2 - cos(5*x)/10
>> int(1/(2*sin(x)-cos(x)))
ans =
-(5^(1/2)*log(tan(x/2 - atan(1/2)/2)))/5
ans = -inf
Виникає проблема. Отримуємо не числову відповідь, а комбінацію функцій, яка фактично не піддається або слабо піддається спрощенню. ans = -2/3*log(2)+2/3*log(31)+2/3*3^(1/2)*atan(11/3*3^(1/2))-2/3*log(7)-2/3*3^(1/2)*atan(5/3*3^(1/2))
>> int([x^3,sin(x),exp(x)],x) ans = [ 1/4*x^4, -cos(x), exp(x)]
За допомогою функції int можна також обчислювати кратні інтеграли або невласні інтеграли (Які мають аналітичний розвязок, тобто в принципі беруться)
Перед обчисленням потрібно виконати команду, яка задає символьні змінні. Це можна зробити за допомогою однієї команди >>syms a x y z
Поиск по сайту: |
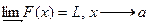
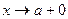
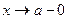 обчислює границю F в точці а зліва або справа
обчислює границю F в точці а зліва або справа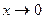

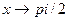
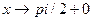
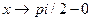
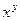
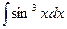 >>int(sin(x)^3,x)
>>int(sin(x)^3,x) >>int(log(2*x),x)
>>int(log(2*x),x)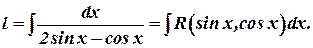
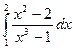 >> int((x^2-2)/(x^3-1),x,1,2)
>> int((x^2-2)/(x^3-1),x,1,2)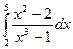 >> int((x^2-2)/(x^3-1),x,2,5)
>> int((x^2-2)/(x^3-1),x,2,5)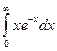 >> int(x*exp(-x),x,0,inf) ans =1
>> int(x*exp(-x),x,0,inf) ans =1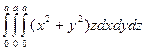 >> int(int(int((x^2+y^2)*z,x,0,a),y,0,a),z,0,a) ans =1/3*a^6
>> int(int(int((x^2+y^2)*z,x,0,a),y,0,a),z,0,a) ans =1/3*a^6