 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Кожному варіанту відповідає своє значення діелектричної проникності e(r)Стр 1 из 5Следующая ⇒
Факультет електроенерготехніки та автоматики
Розрахункова робота з фізики №1 на тему “Електрика і магнетизм” Варіант № 18 Виконала: студентка 1 курсу ФЕА гр. ЕС-61 Ткачук Т.В. Перевірив: Захарченко Р.В. Київ-2007 ЗАВДАННЯ 1 Тема 1. Електричне поле. Електроємність провідника. Конденсатори. 1.2 Номер Вашого варіанта відповідає номеру Вашого прізвища в списку журналу групи. Розрахунки повинні бути виконані в міжнародній системі одиниць (SI); наявність таблиць даних та відображення даних “крапками” на графіках обов’язкове; необхідна кількість розрахованих даних в межах зміни r (або х) від мінімального до максимального значення повинна складати не менше 10-ти (“крапок” на графіку); у випадку, якщо побудова графіків проводиться не за допомогою програмного забезпечення (комп’ютерні програми), а “вручну” – побудова на міліметровому папері обов’язкова. 1.4 Необхідна література: И.В.Савельев “Курс общей физики”, том 2, §§14- 20, §14 “Вычисление полей с помощью теоремы Гаусса»; §20 “Примеры на вычисление поля в диэлектриках”. Завдання для варіантів з №1 по №10 включно Простір між обкладинками сферичного конденсатора заповнений діелектриком, діелектрична проникність якого e(r) є функцією від відстані r між зовнішньою та внутрішньою обкладинками. Радіус внутрішньої сфери ro = 0.5 см, радіус зовнішньої сфери r може змінюватись в межах від ro £ r £ 10× ro . Заряд обкладки конденсатора q = 0.15 нКл. Внутрішня сфера конденсатора заряджена позитивно.
Вивести формули та побудувати графіки залежності від r :
Кожному варіанту відповідає своє значення діелектричної проникності e(r)
Завдання для варіантів з №11 по №20 включно
Простір між обкладинками довгого циліндричного конденсатора, утвореного металевою ниткою радіусом ro = 1.5 мм та співвісною з нею циліндричною металевою поверхнею, заповнений діелектриком з діелектричною проникністю e(r), де r – це відстань від осі циліндра, причому ro< r £ 11× ro . Лінійна густина заряду l = 3,15 × 10-11 Кл/м. Металева нитка заряджена позитивно.
Вивести формули та побудувати графіки залежності від r :
Кожному варіанту відповідає своє значення діелектричної проникності e(r)
ТАБЛИЧКА НА НАСТУПНІЙ СТОРІНЦІ
Завдання для варіантів з №21 по №30 включно
Простір між пластинами плоского конденсатора заповнений діелектриком, діелектрична проникність якого e(х) залежить від х , де х – відстань вздовж нормалі від позитивно зарядженої пластинки. Заряд обкладки q = 3,54 × 10-10 Кл. Площа обкладки S = 100 см2. Максимальна відстань між обкладками конденсатора l = 0.5 см.
Вивести формули та побудувати графіки залежності від х :
Кожному варіанту відповідає своє значення діелектричної проникності e(r)
Приклад 1. Умова задачі: Простір між обкладинками сферичного конденсатора заповнений діелектриком, діелектрична проникність якого e(r) є функцією від відстані r між зовнішньою та внутрішньою обкладинками. Радіус внутрішньої сфери ro = 1,0 см, радіус зовнішньої сфери r може змінюватись в межах від ro £ r £ 10× ro . Заряд обкладки конденсатора q = 0.111 нКл. Внутрішня сфера конденсатора заряджена позитивно.
Вивести формули та побудувати графіки залежності від r :
Розв’язок:
Знайдемо різницю потенціалів U(r) між обкладинками конденсатора :
Для випадку коли ε = 1 , U(r) буде:
Ємність сферичного конденсатора розраховується за формулою:
ЗАВДАННЯ 2
Поиск по сайту: |




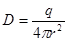




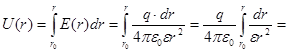




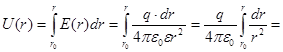 U(r) U(r)
U(r) U(r)

 , U
, U 
