 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Застосування індексного методу в статистичному аналізі соціально-економічних явищ і процесів ⇐ ПредыдущаяСтр 4 из 4
Задача 5.3. На основі даних про розміри середньомісячної заробітної плати та середньоспискову чисельність : - обчислити загальні індекси; - здійснити факторний аналіз фонду оплати праці на підприємстві Зробити висновки за кожним пунктом розрахунків.
Таблиця 5.1 – Вхідні дані
Загальний (зведений) індекс являє собою співвідношення рівнів показника неоднорідної сукупності, елементи якої з причини різної натуральної форми та одиниць вимірювання не підлягають підсумовуванню. Він показує, як у середньому змінився показник по сукупності елементів і позначається великою латинською літерою «І» з порядковим символом, що означає назву показника, зміну якого характеризує даний індекс. Основною проблемою побудови загального індексу є подолання несумірності елементів, що утворюють сукупність, наприклад, продукції, товарів тощо. Для того, щоб привести різні види продукції до порівняльного виду і здійснювати підсумовування різних видів товарів, необхідно здійснити введення в індекс додаткового і незмінного показника, який щільно пов'язаний з індексованою величиною. Цей додатковий показник називають сумірником. Таким сумірником може бути ціна, собівартість чи трудомісткість одиниці продукції. Перемноживши ціну продукції кожного виду на відповідний сумірник, отримують показники, які можна підсумовувати, а також порівнювати їх в цілому по сукупності. Такі індекси називаються агрегатними (від латинського aggregato ‑ приєдную) і позначаються великою латинською літерою «І». Щоб побудувати загальний індекс, який би відображав зміну тільки одного фактора (індексованої величини), необхідно сумірники (ваги) зафіксувати на рівні одного періоду (звітного або базисного). Залежно від того, на якому рівні, звітному чи базисному, фіксують сумірник (вагу), розрізняють дві системи побудови агрегатних індексів: - базисно-зважену, або систему Ласпереса (за прізвищем німецького економіста, який у 1871 році запропонував фіксувати сумірник на рівні базисного періоду). Знайдемо індекс цін таким чином:
Таблиця 5.2 – Розрахунок загального індексу
- поточно-зважену, або систему Пааше (за прізвищем німецького економіста, який у 1874 році запропонував фіксувати сумірник на рівні поточного періоду). Розрахуємо індекс цін:
Таблииця 5.3 – Розрахунок індексу цін
Аналогічно розрахуємо як загалом змінився обсяг продажу товарів групи. За системою Ласпейреса:
Таблиця 5.4 – Розрахунки індексу за системою Ласпейреса
За системою Пааше:
Таблиця 5.5 – Розрахунки індексу за системою Паше
Загальний індекс можна знайти і наступним чином:
Таблиця 5.6 – Розрахунок загального індексу
Висновок: середньомісячна заробітна плата за період зросла на 18%, в тому числі за рахунок зростання загального індексу середньомісячної заробітної плати Ix на 4% та за рахунок зростання загального індексу середньомісячної заробітної плати In на 14%. Тепер знаходимо індекси середнього рівня інтенсивності показника. Індекс змінного складу – являє з себе співвідношення середніх рівнів досліджуваного явища, що відносяться до різних періодів часу. Індекс показує у скільки разів зріс середній рівень інтенсивного показника у звітному періоді порівняно з базисним. Відображає зміну як індексованої величини, так і структури сукупності (ваги). Розрахунок індексу змінного складу здійснюється за формулою:
де
Індекс постійного складу– розраховується за вагами, зафіксованими на рівні певного періоду і відображає зміну тільки індексованої величини. Розраховується за формулою:
Індекс структурних зрушень – характеризує вплив змін структури досліджуваного явища на динаміку середнього рівня цього явища. Розраховується за формулою:
Отже, середньомісячна заробітна плата Індекс структурних зрушень зросла на 2%; середньомісячна заробітна платаІндекс змінного складуза період зросла на 6%; середньомісячна заробітна платаІндекс постійного складу зросла за період на 4% за рахунок зміни заробітних плат окремих працівників та середньоспискової чисельності робітників. Тепер здійснимо факторний аналіз середньої заробітної плати.
Отже, середньомісячна заробітна плата збільшилася на 45,3 грн., що відбулося головним чином за рахунок змін середніх заробітних плат окремих працівників. Тепер здійснимо факторний аналіз фонду оплати праці на підприємстві.
Таким чином, фонд оплати праці зріс на 8070 грн. Головним чином за рахунок підвищення середньомісячної заробітної плати окремих працівників та середньоспискової чисельності робітників.
Поиск по сайту: |
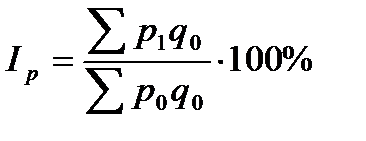 =
=  =104,45%
=104,45% =
= 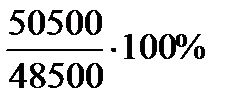 =104,12%.
=104,12%.

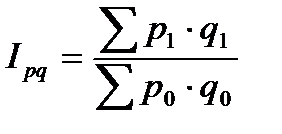
 (5.4)
(5.4) - інтенсивний показник;
- інтенсивний показник; - екстенсивний показник, виражений кількістю чи частотою.
- екстенсивний показник, виражений кількістю чи частотою. (106%)
(106%)
 (104%)
(104%)
 (102%)
(102%)




 =776,9-731,6 = 45,3
=776,9-731,6 = 45,3
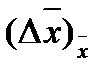 =776,9-746,2 = 30,7
=776,9-746,2 = 30,7 = 746,2-731,6=14,6
= 746,2-731,6=14,6



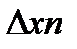 =
=  8070
8070 = (776,9-746,2)*65 = 1995,5
= (776,9-746,2)*65 = 1995,5 = (746,2 – 731,6)*65=949
= (746,2 – 731,6)*65=949 = (65-58)*731,6=5121,2
= (65-58)*731,6=5121,2