 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Геометричний закон розподілу ймовірностей ⇐ ПредыдущаяСтр 2 из 2
Інколи спроби здійснюють до першої появи випадкової події. Число проведених спроб буде цілочисловою випадковою величиною. Цілочислова випадкова величина Х має геометричний закон розподілу, якщо ймовірності її можливих значень
Тут p — імовірність появи випадкової події в кожній спробі — є величиною сталою, q = 1 – p. У табличній формі геометричний закон розподілу такий:
При перевірці умови нормування використовується формула суми нескінченної геометричної прогресії, тому й закон розподілу називають геометричним:
Побудуємо ймовірнісну твірну функцію
Числові характеристики для цього закону:
Серед дискретних випадкових величин лише геометричному закону притаманна властивість відсутності післядії. Це означає, що ймовірність появи випадкової події в k-му експерименті не залежить від того, скільки їх з’явилося до k-го, і завжди дорівнює p. Приклад. Гральний кубик підкидається до першої появи цифри 6. Визначити М(Х), D(X), s(Х) для випадкової величини Х числа здійснюваних підкидань. Розв’язання. Випадкова величина Х є цілочисловою, що має геометричний закон розподілу ймовірностей. За умовою задачі: p = Дістанемо:
Приклад. Спортсмен стріляє зі спортивної рушниці по одній і тій самій мішені. Імовірність влучити в мішень при одному пострілі є величиною сталою і дорівнює 0,8. Стрільба по мішені ведеться до першого влучення. Визначити М(Х), D(X), s(Х) випадкової величини Х — числа витрачених спортсменом набоїв. Розв’язання.Випадкова величина Х є цілочисловою, з геометричним законом розподілу ймовірностей. За умовою задачі: p = 0,8; q = 0,2. Маємо:
Рівномірний закон розподілу ймовірностей. Цілочислова випадкова величина Х має рівномірний закон розподілу, якщо ймовірності її можливих значень обчислюються за формулою:
У табличній формі запису рівномірний закон розподілу має вигляд:
Умова нормування Імовірнісна твірна функція для цього закону
Числові характеристики рівномірного закону:
Приклад.Знайти М(Х), D(X), s(Х), якщо цілочислова випадкова величина Х має рівномірний закон розподілу і можливі значення її такі:
Розв’язання.За умовою задачі маємо: n = 100, Pk = 1/100. Дістаємо:
Поиск по сайту: |
 , k = 1, 2, 3, …, n.
, k = 1, 2, 3, …, n.



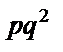


 .
. .
. ;
; .
. ; q =
; q =  .
. ;
;  ;
;  .
. ;
;  ;
;  .
. .
.





 виконується.
виконується. , або
, або  .
. .
.

 .
. .
. .
. .
.