 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Біноміальний закон розподілу ймовірностейСтр 1 из 2Следующая ⇒
План
1. Ймовірнісні твірні функції та їх властивості. 2. Біноміальний закон розподілу ймовірностей. 3. Пуассонівський закон розподілу ймовірностей. 4. Геометричний закон розподілу ймовірностей. 5. Рівномірний закон розподілу ймовірностей. 6. Гіпергеометричний закон розподілу ймовірностей.
Серед дискретних випадкових величин особливе місце в теорії ймовірностей посідають такі, що набувають лише цілих невід’ємних значень Х = хk = 0, 1, 2, 3, ... . Ці випадкові величини називають цілочисловими. Ймовірнісні твірні функції та їх властивості. Для дослідження законів розподілу цілочислових випадкових величин використовують ймовірнісну твірну функцію. Імовірнісною твірною функцією називають збіжний степеневий ряд виду: Тут рk = Р(Х = k), тобто є ймовірність того, що випадкова величина Х набуде значення k = 0, 1, 2, 3, … . Імовірнісній твірній функції притаманні такі властивості 1. А(Х) визначена в кожній точці інтервалу [–1; 1]. 2. При Х = 1 маємо:
де Аk (0) — k-та похідна від А(х), при Х = 0. Отже, знаючи аналітичний вираз для А(х), можемо знайти ймовірність будь-якого можливого значення Х = k. 3. 4. 5.
Біноміальний закон розподілу ймовірностей. Цілочислова випадкова величина X має біноміальний закон розподілу, якщо ймовірність її можливих значень обчислюється за формулою Бернуллі:
У табличній формі цей закон набирає такого вигляду:
При перевірці виконання умови нормування використовується формула біному Ньютона, тому закон розподілу називають біноміальним:
Ймовірнісна твірна функція для біноміального закону
Знайдемо основні числові характеристики для цього закону:
Приклад. У партії однотипних деталей стандартні становлять 95%. Навмання з партії беруть 400 деталей. Визначити Розв’язання.Цілочислова випадкова величина Х має біноміальний закон розподілу ймовірностей, яка може набувати значення Х = k = 0, 1, 2, ..., 400. Імовірності можливих значень обчислюються за формулою Бернуллі: Маємо:
Приклад. У кожному із 100 контейнерів міститься по 8 виробів першого сорту, а решта 2 — браковані. Із кожного контейнера навмання беруть по одному виробу. Визначити М (Х), D (X), s (X) для дискретної випадкової величини Х — поява числа виробів першого сорту серед 100 навмання взятих. Розв’язання.Цілочислова випадкова величина Х має біноміальний закон розподілу. Із умови задачі маємо: n = 100, p = 0,8, q = 0,2, k = 0, 1, 2, 3, ..., 100. Дістаємо:
Поиск по сайту: |
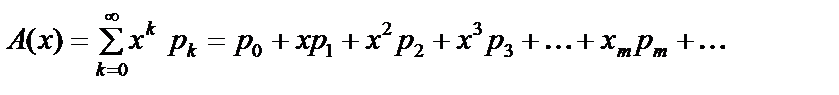 .
. , оскільки це є умовою нормування для дискретної випадкової величини.
, оскільки це є умовою нормування для дискретної випадкової величини.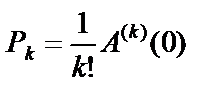 ,
, .
. .
.
 k = 0, 1, 2, 3, ..., n.
k = 0, 1, 2, 3, ..., n.
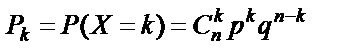
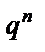




 .
.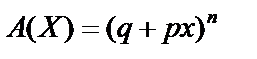 .
.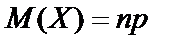 .
. ;
; .
. , де р = 0,95 — імовірність появи стандартної деталі, q = 1 – p =1 – 0,95 = 0,05 — імовірність появи нестандартної деталі.
, де р = 0,95 — імовірність появи стандартної деталі, q = 1 – p =1 – 0,95 = 0,05 — імовірність появи нестандартної деталі. = 400 × 0,95 = 380;
= 400 × 0,95 = 380; = 400 × 0,95 × 0,05 = 19;
= 400 × 0,95 × 0,05 = 19; =
=  » 4,36.
» 4,36. = 100 × 0,8 = 80;
= 100 × 0,8 = 80; = 100 × 0,8 × 0,2 = 16;
= 100 × 0,8 × 0,2 = 16; =
=  » 4.
» 4.