 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теплоємність. Питома й молярна теплоємність. Рівняння Майєра ⇐ ПредыдущаяСтр 3 из 3
Теплоємністю тіланазивається величина, що дорівнює кількості теплоти, яку потрібно передати тілу, щоб підвищити його температуру на один градус Кельвіна. Тобто
де Питомою теплоємністю називають теплоємність одиниці маси речовини
де Молярною теплоємністю називають теплоємність моля речовини .
де Питома й молярна теплоємності пов'язані співвідношенням
Теплоємність залежить від умов, при яких відбувається нагрівання тіла. Найбільш цікавими є теплоємності для випадків, коли нагрівання виконується при сталому об'ємі або при сталому тиску. У першому випадку ми маємо справу з теплоємністю при сталому об'ємі(позначається З’ясуємо зв’язок між внутрішньою енергією та теплоємністю газу. Якщо нагрівання має місце при сталому об'ємі, то тіло не виконує роботу над зовнішніми тілами й, отже, уся теплота йде на збільшення внутрішньої енергії тіла:
У термодинаміці подібні вирази прийнято записувати у вигляді
Символ частинної похідної з індексом Дослідним шляхом установлено, що в газах, які близькі за своїми властивостями до ідеального газу, теплоємність при сталому об'ємі в широких температурних інтервалах практично не залежить від температури:
Інтегруємо це співвідношення і знаходимо вираз для внутрішньої енергії одного моля ідеального газу
(ми врахували, що
Внутрішня енергія – величина адитивна. Тоді внутрішня енергія маси газу
Таким чином, отримали співвідношення (15) для внутрішньої енергії ідеального газу. Знайдемо зв’язок між теплоємностями
(
Відповідно до формули (12) доданок
Ми не робили ніяких припущень про властивості газу, тому формула (16) справедлива для будь-яких газів. Тепер припустимо, що газ ідеальний. Відповідно до рівняння стану ідеального газу (рівняння Менделєєва-Клапейрона)
Підстановка цього значення похідної в (17) приводить до співвідношення
Таким чином, отримали важливе співвідношення між Експериментально більш зручно визначати не
Відношення (19) являє собою характерну для кожного газу величину і називається сталою адіабати. Далі ми встановимо, що значення Знайдемо вираз для внутрішньої енергії через сталу адіабати. Відповідно до рівняння Майєра (18)
звідки
Підставивши цей вираз для
Врахуємо, що у відповідності до рівняння Менделєєва-Клапейрона
Таким чином, отримали ще співвідношення (22) та (23) для внутрішньої енергії ідеального газу.
Поиск по сайту: |
 ,
,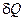 – кількість теплоти, передача якої підвищує температуру тіла на
– кількість теплоти, передача якої підвищує температуру тіла на  . Теплоємність тіла виміряється в джоулях на кельвін (Дж/К).
. Теплоємність тіла виміряється в джоулях на кельвін (Дж/К). ,
, – маса тіла. Виміряється вона в джоулях на кілограм-кельвін (Дж/(кг∙К)).
– маса тіла. Виміряється вона в джоулях на кілограм-кельвін (Дж/(кг∙К)). ,
, – кількість молів речовини тіла. Виміряється вона в джоулях на моль-кельвін (Дж/(моль∙К)).
– кількість молів речовини тіла. Виміряється вона в джоулях на моль-кельвін (Дж/(моль∙К)). . (11)
. (11) ), у другому – з теплоємністю при сталому тиску(
), у другому – з теплоємністю при сталому тиску( 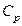 ).
). (див. формулу першого закону термодинаміки; індекс
(див. формулу першого закону термодинаміки; індекс 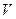 біля
біля 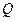 підкреслює ту обставину, що теплота передається в умовах, коли об'єм тіла не змінюється). Звідси випливає, що молярна теплоємність будь-якої речовини при сталому об'ємі дорівнює
підкреслює ту обставину, що теплота передається в умовах, коли об'єм тіла не змінюється). Звідси випливає, що молярна теплоємність будь-якої речовини при сталому об'ємі дорівнює . (12)
. (12) . (13)
. (13) за змінною
за змінною  об'єм вважається сталим.
об'єм вважається сталим. . Тоді відповідно до формули (12)
. Тоді відповідно до формули (12) .
.
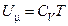 . (14)
. (14) . (15)
. (15) . Будемо розглядати процес, коли теплота передається газу при сталому тиску:
. Будемо розглядати процес, коли теплота передається газу при сталому тиску: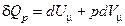
 – об'єм моля; індекс
– об'єм моля; індекс 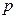 біля
біля  , прийдемо до формули для молярної теплоємності газу при сталому тиску:
, прийдемо до формули для молярної теплоємності газу при сталому тиску: .
.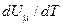 дорівнює молярній теплоємності при сталому об'ємі. Урахувавши це, прийдемо до співвідношення
дорівнює молярній теплоємності при сталому об'ємі. Урахувавши це, прийдемо до співвідношення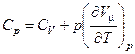 . (16)
. (16) . Диференціюємо цей вираз за величиною
. Диференціюємо цей вираз за величиною  , й отримаємо
, й отримаємо . (17)
. (17) . (18)
. (18) . (19)
. (19) визначається числом і характером ступенів вільності молекул.
визначається числом і характером ступенів вільності молекул. , (20)
, (20) . (21)
. (21) . (22)
. (22) прийдемо до ще одного виразу для внутрішньої енергії довільної маси ідеального газу:
прийдемо до ще одного виразу для внутрішньої енергії довільної маси ідеального газу: . (23)
. (23)