 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Робота, що виконується тілом при змінах його об'ємуСтр 1 из 3Следующая ⇒
Внутрішня енергія термодинамічної системи Внутрішньою енергієюназивають повну енергію тіла за винятком кінетичної енергії тіла як цілого і потенціальної енергії тіла в зовнішньому полі сил. Отже, внутрішня енергія складається з кінетичної енергії хаотичного руху молекул, потенціальної енергії взаємодії між ними і внутрішньомолекулярної енергії. У термодинамічні формули входить не сама енергія, а її зміна, що пов’язана зі зміною деякого параметра. Тому внутрішню енергію можна визначати з точністю до довільної адитивної сталої, вибираючи її так, щоб вираз для енергії був простим. Так, зазвичай вивчаються процеси, при яких внутрішньомолекулярна енергія залишається постійною. Тому цю енергію у внутрішній енергії можна не враховувати. Внутрішня енергія системи тіл складається із внутрішньої енергії кожного з окремих тіл й енергії взаємодії між тілами. Остання являє собою енергію взаємодії в тонкому шарі на границі між тілами. Вона є малою у порівнянні з енергією окремих макроскопічних тіл. Тому нею можна знехтувати й вважати, що внутрішня енергія системи макроскопічних тіл дорівнює сумі внутрішніх енергій цих окремих тіл. Отже, внутрішня енергія є величина адитивна. Внутрішня енергія є функцією стану системи. Це означає, що незалежно від попередньої історії системи її енергія в даному стані має визначені йому значення. Тому збільшення внутрішньої енергії при переході системи з одного стану в інший завжди дорівнює різниці значень внутрішньої енергії в кінцевому й початковому станах незалежно від шляху (процесу), за яким відбувався перехід системи з одного стану в інший.
Робота, що виконується тілом при змінах його об'єму
Розглянемо газ у циліндрі з поршнем (рис.1). Знайдемо нескінченно малу або елементарну роботу
тому що збільшення об'єму дорівнює Вираз (1) є справедливим й у загальному випадку квазистатичної зміни об'єму будь-якого тіла, що знаходиться під постійним зовнішнім тиском. Слід підкреслити, що величина (1) є алгебраїчною. При розширенні тіла збільшення об'єму Формула (1) визначає елементарну роботу, виконану газом при нескінченно малому збільшенні об'єму. Робота, виконана при скінченних змінах об'єму, обчислюється шляхом підсумовування елементарних робіт, тобто шляхом інтегрування:
де
Квазистатичний процес зміни об'єму тіла можна зобразити на діаграмі З рис. 3 випливає, що робота, яка виконується при квазистатичному круговому процесі, чисельно дорівнює площі, яка охоплюється кривою, що зображує цикл, узятої зі знаком плюс, коли обхід по кривій відбувається за годинниковою стрілкою, і зі знаком мінус, коли обхід по кривій відбувається проти годинникової стрілки.
Знайдемо роботу газу в різних ізопроцесах: Ізохорний. Так як V = const, dV = 0. Тому dAV =0 і АV = 0 (3) Ізобарний. Р = const. Взявши до уваги рівняння Клапейрона-Менделєєва, одержимо
Ізотермічний. Т = const.
Поиск по сайту: |

 , виконану газом при нескінченно малому квазистатичному розширенні, у якому його об'єм збільшується на
, виконану газом при нескінченно малому квазистатичному розширенні, у якому його об'єм збільшується на  . Сила тиску газу на поршень дорівнює
. Сила тиску газу на поршень дорівнює  , де
, де  – площа поршня. Якщо поршень переміститься на відстань
– площа поршня. Якщо поршень переміститься на відстань  , то газ виконає роботу
, то газ виконає роботу  або
або , (1)
, (1) .
. , (2)
, (2) – робота, виконана тілом при квазистатичній зміні об'єму тіла від значення
– робота, виконана тілом при квазистатичній зміні об'єму тіла від значення  до значення
до значення  . Зазначимо, що таке обчислення можливе тільки тоді, коли тиск є певною функцією об'єму
. Зазначимо, що таке обчислення можливе тільки тоді, коли тиск є певною функцією об'єму 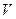 . Тим часом, відповідно до рівняння стану,
. Тим часом, відповідно до рівняння стану, 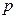 залежить не тільки від об’єму
залежить не тільки від об’єму  . Змінюючи неоднаково в ході процесу температуру, можна квазистатично перевести систему з початкового стану в кінцевий різними способами. Кожному із цих способів відповідає своя функція
. Змінюючи неоднаково в ході процесу температуру, можна квазистатично перевести систему з початкового стану в кінцевий різними способами. Кожному із цих способів відповідає своя функція  і своє значення інтеграла у формулі (2). Таким чином, робота А не визначається початковим й кінцевим станами системи. Її величина залежить також і від способу або шляху переходу системи з початкового стану в кінцевий. Про величини такого роду говорять, що вони не є функціями стану. Навпаки, величини, що мають цілком певні значення в кожному стані системи, називаються функціями стану. Функціями стану є, наприклад, температура системи при термодинамічній рівновазі, внутрішня енергія. Саме тому елементарну роботу позначають через
і своє значення інтеграла у формулі (2). Таким чином, робота А не визначається початковим й кінцевим станами системи. Її величина залежить також і від способу або шляху переходу системи з початкового стану в кінцевий. Про величини такого роду говорять, що вони не є функціями стану. Навпаки, величини, що мають цілком певні значення в кожному стані системи, називаються функціями стану. Функціями стану є, наприклад, температура системи при термодинамічній рівновазі, внутрішня енергія. Саме тому елементарну роботу позначають через  .
.
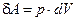 чисельно дорівнює площі заштрихованої смужки
чисельно дорівнює площі заштрихованої смужки
 (рис. 2). Тоді робота, яка виконується тілом при зміні його об'єму від значення
(рис. 2). Тоді робота, яка виконується тілом при зміні його об'єму від значення  і прямими
і прямими 
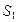 , заштрихованій лініями, які нахилені вправо, взятої зі знаком плюс
, заштрихованій лініями, які нахилені вправо, взятої зі знаком плюс 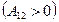 . Робота
. Робота 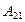 на ділянці 2–1чисельно дорівнює площі
на ділянці 2–1чисельно дорівнює площі  , заштрихованої лініями, нахиленими вліво, взятої зі знаком мінус
, заштрихованої лініями, нахиленими вліво, взятої зі знаком мінус  . Робота за цикл дорівнює
. Робота за цикл дорівнює  , тобто чисельно дорівнює площі циклу. При зворотному напрямку циклу знаки робіт змінюються на зворотні
, тобто чисельно дорівнює площі циклу. При зворотному напрямку циклу знаки робіт змінюються на зворотні
 (4)
(4) . (5)
. (5)