 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 10. Числові методи ⇐ ПредыдущаяСтр 3 из 3
1. Елементарна теорія похибок. 2. Наближені методи розв’язування рівнянь та систем рівнянь.
10.1.Елементарна теорія похибок
Означення. Нехай A ‑ точне значення деякого числа, тоді як a ‑ наближене. Тоді різниця Da = |A-a| називається абсолютною похибкою числа A . Означення. Частка da= Приклад. Нехай A=10; a=9,5; B=50; b=50,5. Тоді Da = |10-9,5| = 0,5; da = 0,5/10 =0,05 = 5%. Db = |50-50,5| = 0,5; db = 0,5/50 = 0,01 = 1%. Зазначимо, що на практиці більшість статистичних даних є відомими лише з деякою похибкою. Означення.Кажуть, що число a має n вірних знаків (розрядів, цифр), якщо його абсолютна похибка не перевищує половини n-го розряду. Приклад. Числа 10±0,5 та 50±0,5 мають два вірні знаки. Число 123,2±0,05 має чотири вірні знаки. У математиці (а також в її застосуваннях) прийнято записувати для кожного числа всі його вірні знаки і лише ці вірні знаки. Наприклад, за записом x1=112,40 визначаємо, що це число має п’ять вірних знаків ( D=0,005 ), тоді як за записом числа x2=112,4 визначаємо той факт, що це число має чотири вірні знаки (D=0,05). У числі y1=1200 вірними є чотири знаки (D=0,5), а в числі y2=0,120×104 маємо тільки три (D=5).
Теорема 1. У разі додавання (віднімання) наближених чисел їхні абсолютні похибки додають: Da+b £ Da + Db . Теорема 2. У разі множення (ділення) наближених чисел їхні відносні похибки додають: da×b £ da + db . Для додавання багатьох близьких чисел (a1~a2~…~an~a) використовують формулу
Приклад. Нехай a=12±0,3 ; b=10±0,2. Виконавши додавання, одержимо a+b=22±0,5 , звідки Da+b = 0,5. У результаті множення отримуємо a×b=(12±0,3)×(10±0,2)»120±5,4 , звідки Абслютну похибку Dy функції від багатьох змінних y = y(x1,…,xn), як зазначено в темі 6, обчислюють за формулою
Типовою помилкою економіста є наведення у відповіді великої кількості знаків після коми (оскільки комп’ютер виконує обчислення з багатьма розрядами). Проте точність результату не може бути вищою, ніж точність вхідних даних! Зазначимо, що у разі віднімання відносна похибка може значно зростати. Приклад. Нехай a=121±0,5 b=119±0,5 Відносні похибки аргументів становлять та Знаходимо відносну похибку результату віднімання наближених чисел: Як бачимо, внаслідок виконання лише однієї дії відносна похибка зросла більше, ніж у 100 разів. Отже у разі виконання значної кількості обчислень завжди є небезпека втрати вірних знаків. Автоматизація розрахунків за допомогою комп’ютера в цьому аспекті допомогти аж ніяк не може. Користувач сам повинен планувати процес обчислень так, щоб уникати віднімання близьких чисел.
10.2. Наближені методи розв’язування рівнянь та систем рівнянь
Розглянемо рівняння з одним невідомим f(x) = 0. Точних методів відшукання всіх коренів такого рівняння немає. Наближені методи полягають у виконанні двох етапів. Етап 1. відокремлення коренів. Необхідно знайти відрізок [a;b] , на якому рівняння f(x)=0 має тільки один корінь (рис.10.1).
a b Рис. 10.1.
Етап відокремлення коренів виконується вручну за допомогою загальновідомих методів дослідження функцій (тема 4). На цьому етапі корисною може бути наведена нижче теорема. Теорема. Якщо функція y=f(x) є неперервною на відрізку [a;b], причому величини f(a) та f(b) мають різні знаки, то на [a;b] рівняння f(x)=0 має хоча б один корінь. Якщо, крім того, похідна f¢(x) на [a;b] не змінює знака, то цей корінь є єдиним. Етап 2. уточнення коренів. Розглянемо один з найпростіших методів уточнення відділеного кореня – метод половинного ділення. Обчислюємо значення f(x) в середині відрізка [a;b], тобто в точці Зрозуміло, що другий етап наближеного відшукання кореня бажано виконувати за допомогою комп’ютера. Алгоритм методу половинного ділення, з використанням шкільних конструкцій алгоритмічної мови, можна записати так:
ввід інтервалу (a;b) та потрібної точності (D) поки |a-b| < D виконувати пц
якщо f(a)×f(b) > 0 то a:=c інакше b:=c кц вивід значення кореня
Розглянемо систему лінійних рівнянь
Метод Жордана-Гауса (як і інші точні методи) полягає у виконанні досить багатьох дій, у тому числі й операцій віднімання. Отже, знайдені таким методом корені (x1,…,xn) насправді виявляються досить неточними. Розглянемо один з методів уточнення коренів для систем лінійних рівнянь – метод ітерації. Згідно з цим методом систему (10.1) записують у вигляді
Початковим наближенням системи (10.2) є точка Застосовують таку обчислювальну схему:
Теорема. Якщо Загалом, на практиці досить часто застосовують такий підхід: спершу одним з точних методів відшукують наближені значення коренів, потім якимось з наближених методів поліпшують значення цих коренів до потрібного рівня точності.
Контрольні запитання
1. Операції над матрицями, їхні властивості. 2. Операції над векторами. Добуток матриці на вектор. 3. Розв’язування систем лінійних рівнянь за допомогою оберненої матриці. 4. Визначник другого та третього порядку, його властивості. 5. Обчислення визначника n-го порядку за допомогою алгебраїчних доповнень. 6. Система двох лінійних рівнянь з двома невідомими. 7. Система двох лінійних рівнянь з трьома невідомими 8. Система трьох лінійних рівнянь з трьома невідомими 9. Розв’язування систем лінійних рівнянь за допомогою формул Крамера. 10. Власні числа та власні вектори матриці. 11. Модель міжгалузевого балансу (Леонтьєва). 12. Рівняння прямої на площині (загальне; у відрізках; через дві точки). 13. Криві другого порядку, їхні рівняння. 14. Рівняння площини (через три точки, у відрізках, через точку перпендикулярно до вектора). 15. Рівняння прямої у просторі (через дві точки; параметричне; канонічне). 16. Кут між прямими (на площині та у просторі). Кут між прямою та площиною. 17. Послідовність, границя послідовності. 18. Геометрична прогресія, її сума. Нескінченна геометрична прогресія. 19. Формула розрахунку майбутньої вартості теперішніх грошей. 20. Формула розрахунку теперішньої вартості майбутніх грошей. 21. Формула розрахунку рент. 22. Лінійна, квадратична та кубічна функції, їхні графіки. Економічний сенс. 23. Показникова функція, її графік. Економічний сенс. 24. Степенева функція, її графік. Економічний сенс. 25. Границя функції. Властивості границь. 26. Число e. 27. Логістична крива, її графік. Економічний сенс. 28. Означення похідної. 29. Правила знаходження похідних. 30. Необхідна умова екстремуму. 31. Перша достатня умова екстремуму. 32. Друга достатня умова екстремуму. 33. Випуклі та увігнуті функції. Точка перегину. 34. Достатня ознака випуклості функції. 35. Достатня ознака існування точки перегину. 36. Похідна як гранична зміна економічного показника. 37. Обчислення темпу приросту та еластичності за допомогою похідної. 38. Функції багатьох змінних. Лінії рівня. 39. Часткова похідна. Означення. 40. Невизначений інтеграл. Означення. Властивості. 41. Обчислення інтеграла методом заміни змінних. 42. Інтегрування за частинами. 43 Визначений інтеграл. Означення. Властивості. 44. Геометричний сенс визначеного інтеграла. 45. Невласний інтеграл. 46. Диференціальні рівняння з розділеними змінними. 47. Лінійні диференціальні рівняння першого порядку. 48. Лінійні диференціальні рівняння другого порядку зі сталими коефіцієнтами. 49. Задача Коші. 50. Сума нескінченного ряду. Властивості збіжних рядів. 51. Ознака Даламбера збіжності рядів. 52. Ознака Лейбніца збіжності рядів. 53. Абсолютна збіжність рядів. 54. Степеневий ряд. Область збіжності. 55. Розклад елементарних функцій у степеневий ряд. 56. Абсолютні та відносні похибки арифметичних дій. 57. Метод половинного ділення розв’язування нелінійних рівнянь. 58. Метод ітерацій розв’язування систем лінійних рівнянь. 59. Метод прямокутників обчислення визначених інтегралів.
60. Розкласти в степеневий ряд функцію y=e-x. 61. Виконати операцію множення матриць другого або третього порядку. 62. Обчислити визначник третього порядку за допомогою алгебраїчних доповнень. 63. За допомогою формул Крамера розв’язати систему трьох лінійних рівнянь з трьома невідомими. 64. Записати рівняння прямої на площині (у відрізках), яка проходить через точки (2;3) та (6;8). 65. Записати рівняння прямої у просторі, яка проходить через дві точки . 66. Записати рівняння площини, яка проходить через три точки. 67. Знайти границі послідовностей 68. Знайти границі функцій 69. Нараховують складні відсотки у розмірі 20%. Обчислити майбутню вартість (через три роки) теперішніх грошей у сумі 1000 грн. 70. Знайти похідну від функції y=2×x×e3x-1+(1/8)ln2(x+3); y=(1+ex)/(1-ex). 71. Знайти точки перегину та інтервали випуклості функції y=2×x3-3×x2+15. 72. Обчислити часткові похідні від функцій z=x3×y2-2×x×y3 ; z=ln(x2+2×y3). 73 Обчислити інтеграл 74. Інтегруванням за частинами обчислити інтеграл 75. Обчислити визначений інтеграл 76. Розв’язати диференціальне рівняння
77. Розв’язати задачу Коші (1+y2)dx + x×ydy = 0 ; y(1)=0. 78. Дослідити збіжність ряду 79. Знайти область збіжності степеневого ряду 80. Відносні похибки чисел a та b дорівнюють 4%. Знайти відносну похибку числа a×b.
СПИСОК ЛІТЕРАТУРИ
1. Барковський В., Барковська Н. Математика для економіста. – К., 1997.‑ Т.1‑3. 2. Бугір М. Математика для економістів. – Тернопіль, 1998. 3. Михайленко В., Федоренко Н. Математичний аналіз для економістів. – К., 1999. 4. Нікбахт Е., Гроппелі А. Фінанси. ‑ К., 1993. 5. Nicholson R.N. Mathematics for Business and Economics. ‑ 1986. 6. Завада О. Методичні вказівки до виконання контрольних робіт з курсу “Математика для економіста”. – Львів, 2000.
З М І С Т Вступ 3 Частина 1 4 Тема 1. Лінійна алгебра 4 Тема 2. Аналітична геометрія 21 Тема 3. Послідовності 32 Тема 4. Функції від однієї змінної 40 Тема 5. Диференціальне числення 49 Частина 2 59 Тема 6. Функції від багатьох змінних 59 Тема 7. Інтегральне числення 70 Тема 8. Диференціальні рівняння 82 Тема 9. Числові та степеневі ряди 92 Тема 10. Числові методи 97 Контрольні запитання 101 Список літератури 104
Поиск по сайту: |
 називається відносною похибкою числа A.
називається відносною похибкою числа A.
 .
.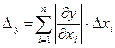 .
.
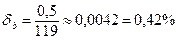 .
.
 y
y
 [ ] x
[ ] x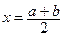 . Залежно від значення
. Залежно від значення 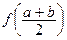 вибираємо ту частину інтервалу [a;b], де знаки функції f(x) є різними. Отже, інтервал, у якому є корінь, зменшився удвічі. Продовживши процес, ми звужуємо інтервал до такої величини, поки його розмір (який дорівнює абсолютній похибці) не стане меншим від потрібної нам величини.
вибираємо ту частину інтервалу [a;b], де знаки функції f(x) є різними. Отже, інтервал, у якому є корінь, зменшився удвічі. Продовживши процес, ми звужуємо інтервал до такої величини, поки його розмір (який дорівнює абсолютній похибці) не стане меншим від потрібної нам величини.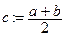
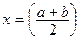
 . (10.1)
. (10.1) . (10.2)
. (10.2) .
. . (10.3)
. (10.3)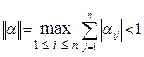 , то зі збільшенням кількості кроків k вектор
, то зі збільшенням кількості кроків k вектор  збігається до точного розв’язку
збігається до точного розв’язку  .
.
 ;
; 
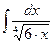 ,
, 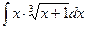 ,
, 
 ;
; 
 ;
;  ;
;  ,
, 
 ;
;  ;
; ;
;  .
. ;
; 
