 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 6. Функції від багатьох зміннихСтр 1 из 3Следующая ⇒
Частина 2
1. Поняття функції від багатьох змінних. Лінії рівня. 2. Частинні похідні. Повний диференціал. 3. Знаходження екстремуму функції від багатьох змінних.
6.1. Поняття функції від багатьох змінних. Лінії рівня На практиці досить часто функція y залежить не від однієї змінної x, а від багатьох аргументів x1,…,xn. Означення. Множина значень {x1,…,xn}, за яких вираз f(x1,…,xn) має зміст, називається областю визначення функції від n змінних y = f(x1,…,xn). Приклади. 1. Функція від двох змінних z=3x+5xy+y2. Область визначення цієї функції - всі пари дійсних чисел (x;y). 2. Функція від чотирьох змінних y=2x1+3x2-x3+7x4. 3. Функція від трьох змінних V=V(a,b,c)=a×b×c. Об’єм паралелепіпеда є функцією від довжин його сторін. 4. Функція від двох змінних Q=F(K,L). Обсяг випущеної продукції Q є функцією від кількості затраченого капіталу K та кількості затраченої праці L. Областю визначення цієї функції є множина {K³0; L³0}. 5. Область визначення функції
z
x Рис. 6.1. Функції від двох змінних геометрично зображають також за допомогою ліній рівня (ліній однакового рівня, ізоліній). Означення. Лінією рівня функції від двох змінних z=f(x,y) називається множина точок площин OXY таких, що f(x,y)=const=C. Прикладом ізоліній є паралелі та меридіани. Приклади. 1. Побудуємо лінії однакового рівня функції При C=6 отримуємо При C=8 отримуємо ізолінію (неявну функцію y від x) x2+y2=62.
6 8 10 x Рис. 6.2. 2. Для випуску продукції Q використовують ресурси x1 та x2. Виробнича функція має вигляд Q=10x1+20x2 (ресурси повністю взаємозамінні, наприклад, цвяхи та шурупи). Зобразити ізолінії для Q=Q(x1,x2) (лінії однакової кількості (quantity) продукції, ізокванти ). Очевидно, що при C=60 ізолінія (ізокванта) – це відрізок прямої 10x1+20x2=60, а при C=40 – відрізок прямої 10x1+20x2=40 (рис. 6.3).
(Ресурс x1)
Рис. 6.3. 3. Виробнича функція має вигляд Q=min{10x1,20x2} (ресурси повністю взаємодоповнюючі, наприклад, калійні та азотні добрива). Тоді в точках (x1=2, x2=1), (x1=4, x2=1), (x1=2, x2=3) значення Q=40. У точках (x1=4; x2=2) та (x1=4; x2=4) випуск набуває значення Q=80. На рис. 6.4 зображені лінії однакового рівня (ізокванти) для кількості продукції Q.
1 2 3 4 5 (Ресурс x2)
Рис. 6.4.
Зазначимо, що в другому та третьому прикладах зобразити функцію Q=Q(x1,x2) геометрично в тривимірному просторі дуже складно. 4. Випуск продукції Q, як функцію від вкладеного капіталу K та кількості затраченої праці L, задається формулою Q=K0.6×L0.4 (часткова взаємозамінність і часткова взаємодоповнюваність ресурсів). На рис. 6.5 зображено лінії однакового значення Q (тобто, графіки неявних функцій K0.6×L0.4=10 та K0.6×L0.4=20):
Q=20 Q=10
Рис. 6.5.
L Рис. 6.6. 5. Розглянемо виробничу функцію Кобба-Дугласа вигляду Q=Ka×L1-a (0<a<1) і побудуємо лінії однакового рівня для різних значень параметрів a та C. При a=0,5 та C=2 маємо 2 = K0.5×L0.5 , звідки K= 2L-1. При a=0,3 та C=1 отримуємо 1 = K0.3×L0.7 , звідки K= 2L-7/3. На рис. 6.7 зображені лінії однакового рівня за даних значень a та C.
a=0,5 ; C=2
a=0,3 ; C=1
Рис. 6.7.
6. Нехай виробнича функція Кобба-Дугласа має вигляд Q=Ka×Lb (0<a,b<1). На рис. 6.8,а та 6.8,б показані тривимірні зображення цієї функції (та лінії однакового рівня) для випадків a+b<1 та a+b>1, відповідно.
L L а б Рис. 6.8.
6.2. Частинні похідні. Повний диференціал Означення. Нехай задано функцію z=f(x,y) і нехай деяку точку з області визначення цієї функції (x,y). Якщо аргумент x отримує приріст dx, а аргумент y – приріст dy, то вираз dz=f(x+dx,y+dy)-f(x,y) називають повним приростом функції f(x,y) . Означення. Функція f(x,y) називається неперервною у точці (x0,y0), якщо
Попередні означення легко переносяться із випадку двох змінних на випадок функції від n (n>2) змінних. Означення. Величини dxz=f(x+dx,y)-f(x,y) та dyz=f(x,y+dy)-f(x,y) називаються частинними приростами функції f(x,y) . Означення. Частинною (частковою) похідною від функції f(x,y) за аргументом x називається границя Частинну (часткова) похідну від функції f(x,y) за аргументом y визначаєють аналогічно. Для частинних похідних від функції f(x,y) використовують такі позначення : f¢x(x,y); z¢x; f¢y(x,y); z¢y; Частинні похідні Приклади 1. Нехай Тоді
(Випуск продукції зростає зі збільшенням затрат як капіталу, так і праці).
3. Побудуємо другі частинні похідні від функції Q=K0.6×L0.4 .
(Граничний випуск продукції спадає зі збільшенням як затрат капіталу, так і затрат праці). 4. Знайдемо змішані частинні похідні другого порядку :
Теорема: Якщо функція z = f(x,y) та її похідні z¢x , z¢y , z¢¢xy і z¢¢yx неперервні в точці (x,y) та деякому околі цієї точки, то z¢¢xy = z¢¢yx . Означення. Повним диференціалом dz від функції z =f(x,y) називають суму її частинних диференціалів :
Приклад. Тоді Поняття повного диференціала має ряд застосувань. По-перше, величина dz є приростом (по z) дотичної площини до поверхні z =f(x,y), аналогічно до того, як диференціал dy від функції f(x) є приростом ординати дотичної до кривої y = f(x) (рис. 6.9,а - б).
x a б Рис. 6.9.
де По-третє, з використанням диференціала можна знаходити похідні від функцій, заданих неявно.
Приклад. Нехай Маємо
Отже,
Нехай потрібно знайти похідну
звідки Приклад. Знайти похідну Маємо
звідки
За допомогою неявних похідних в економіці визначають граничні норми (частки, квоти, rate) заміни. Приклад. Виробнича функція має вигляд Q=10x1+15x2, де x1 та x2 -затрати ресурсів (факторів виробництва). Потрібно знайти граничну норму технологічної заміни ресурсу x2 на ресурс x1 (під граничною нормою технологічної заміни ресурсу x2 на ресурс x1 в економіці розуміють додаткову кількість ресурсу x1, яка компенсує зменшення ресурсу x2 на одиницю). Очевидно, що ця гранична норма (MRTS) технологічної заміни в неперервному випадку є похідною від змінної x1 за змінною x2 за умови сталого випуску Q:
Отже, у разі зменшення кількості ресурсу x2 на одиницю та одночасного збільшення ресурсу x1 на 1,5 одиниці випуск Q залишиться не змінниться (рис. 6.10).
x2
1,5 Рис. 6.10. Приклад. Виробнича функція має вигляд Q=K0,6×L0,4 (функція Кобба-Дугласа). Гранична норма (частка) технологічної заміни праці капіталом у цьому випадку с
Як бачимо із останньої формули, значення MRTS (marginal rate of technological substitution) для функції Кобба-Дугласа залежить від співвідношення K/L.
6.3. Знаходження екстремуму функції від багатьох змінних
Означення. Точка За аналогією із функцією від однієї змінної, для функції від двох змінних
Як і раніше, ці умови не обов’язково є достатніми. Отже, відшукання екстремумів функції від багатьох змінних
розв’язати її, знайшовши критичні (стаціонарні) точки Означення. Вектор називається градієнтом функції Очевидно, що градієнт задає напрям найшвидшого зростання функції Очевидно також, що необхідну умову екстремуму можна записати так:
Розглянемо достатні умови екстремуму для випадку функції від багатьох змінних.
Теорема (без доведення). Нехай функція При D = AC-B2<0 екстремуму немає (перегин, сідлова точка, тощо).
Зазначимо, що невиконання достатніх умов не означає того, що екстремуму немає.
Приклад. Знайти екстремум функції z = x3+y3-3xy. Маємо Розв’язуємо систему звідки знаходимо дві критичні (стаціонарні) точки: M0=(0,0) та M1(1,1). Обчислюємо другі частинні похідні:
У точці M0=(0,0) маємо: A=0, B= -3, C=0, отже, AC-B2 = -9<0, тобто екстремуму немає. У точці M1(1,1) маємо: A=6, B= -3, C=6, отже, AC-B2=27>0, A=6>0. Функція z = z(x,y) має мінімум у точці (1,1) .
Розглянемо, накінець, достатні умови існування екстремуму функції від n (n>2) змінних y=f(x1…xn). Знаходимо всі можливі другі частинні похідні і будуємо матрицю (матрицю Гессе).
Означення. Матриця H=H(x1…xn) називається додатно визначеною в точці ( M1 =
…………………………. (6.5)
Означення. Матриця H=H(x1…xn) називається від’ємно визначеною, якщо M1>0, M2<0, M3>0,…,(-1)nMn>0. У темі 1 сформульовано теорему про те, що матриця є додатно визначеною тоді і тільки тоді, коли всі її власні числа є додатними. Правильно й таке: матриця є від’ємно визначеною тоді і тільки тоді, коли всі її власні числа є від’ємними. Теорема . Нехай функція z = f(x1…xn) визначена в околі точки ( Тоді в разі додатної визначеності матриці Гессе (A>0, AC-B2>0, …) в точці (
Зазначимо, що задача відшукання найбільшого і найменшого значення функції від багатьох змінних у деякій замкнутій області відрізняється від задачі знаходження екстремумів. Спеціальні методи вивчають в курсі “Математичне програмування”.
Поиск по сайту: |
 визначається з нерівності 100-x2-y2³0, тобто x2+y2£102. Це круг з центром у початку координат і радіусом r = 10.
визначається з нерівності 100-x2-y2³0, тобто x2+y2£102. Це круг з центром у початку координат і радіусом r = 10. Функція від двох змінних (аргументів) f(x,y) представляє собою деяку поверхню в трьохвимірному просторі. Зокрема, графіком функції
Функція від двох змінних (аргументів) f(x,y) представляє собою деяку поверхню в трьохвимірному просторі. Зокрема, графіком функції  є верхня половина сфери (рис. 6.1).
є верхня половина сфери (рис. 6.1).



 6 8 10 y
6 8 10 y . При C=0 маємо
. При C=0 маємо  тобто x2+y2=102 (коло з радіусом r=10, рис.6.2).
тобто x2+y2=102 (коло з радіусом r=10, рис.6.2). тобто x2+y2=82 . Отже лінією рівня, яка відповідає константі C=6, є коло з радіусом r = 8.
тобто x2+y2=82 . Отже лінією рівня, яка відповідає константі C=6, є коло з радіусом r = 8.
 y
y

 4 Q=60
4 Q=60 3
3
 2 Q=40
2 Q=40 1
1 1 2 3 4 5 6 (Ресурс x2)
1 2 3 4 5 6 (Ресурс x2) (Ресурс x1)
(Ресурс x1)
 5
5

 2 Q=80
2 Q=80

 1 Q=40
1 Q=40


 K
K L
L  У тривимірному просторі функція Q=K0.6×L0.4 є поверхнею, що зображена на рис. 6.6.
У тривимірному просторі функція Q=K0.6×L0.4 є поверхнею, що зображена на рис. 6.6. Q
Q

 K
K
 K
K
 L
L
 a+b<1 a+b>1
a+b<1 a+b>1 Q Q
Q Q










 K K
K K

 .
. (6.1)
(6.1) ;
; .
. та
та  задають напрями дотичних до поверхні z = f(x,y). Варто пригадати, що звичайна похідна f¢(x) =
задають напрями дотичних до поверхні z = f(x,y). Варто пригадати, що звичайна похідна f¢(x) =  задає напрям дотичної до кривої y = f(x).
задає напрям дотичної до кривої y = f(x).







 (6.2)
(6.2)



 z y y=f(x)
z y y=f(x)


 z=z(x,y) dy
z=z(x,y) dy




 dz
dz
 dy Dx=dx
dy Dx=dx






 dx y x
dx y x
 ,
,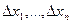 - похибки аргументів.
- похибки аргументів.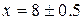 та
та  . Потрібно оцінити похибку функції
. Потрібно оцінити похибку функції  .
.

 у тому випадку, коли функція
у тому випадку, коли функція  задана неявно у вигляді
задана неявно у вигляді  . Узявши від функції F(x,y) повний диференціал, отримуємо
. Узявши від функції F(x,y) повний диференціал, отримуємо
 .
. якщо
якщо 

 .
. .
.



 x1
x1 .
. називається точкою максимуму (мінімуму) функції
називається точкою максимуму (мінімуму) функції  , якщо існує окіл точки
, якщо існує окіл точки  такий, що для всіх точок цього околу виконується нерівність
такий, що для всіх точок цього околу виконується нерівність  (відповідно
(відповідно  ).
). маємо такі необхідні умови екстремуму:
маємо такі необхідні умови екстремуму: (6.3)
(6.3) полягає в тому, що потрібно побудувати систему рівнянь
полягає в тому, що потрібно побудувати систему рівнянь ,
, , які надалі треба перевірити на наявність максимуму чи мінімуму.
, які надалі треба перевірити на наявність максимуму чи мінімуму. (6.4)
(6.4) .
. .
. .
.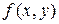 визначена в деякому околі точки
визначена в деякому околі точки  і f¢x(x0,y0)= f¢y(x0,y0)=0. Нехай A= f¢¢xx(x0,y0), B = f¢¢xy(x0,y0) та C = f¢¢yy(x0,y0) неперервні. Тоді при D = AC-B2 > 0 у точці (x0,y0) функція має екстремум (при A<0 – максимум, при A>0 – мінімум ).
і f¢x(x0,y0)= f¢y(x0,y0)=0. Нехай A= f¢¢xx(x0,y0), B = f¢¢xy(x0,y0) та C = f¢¢yy(x0,y0) неперервні. Тоді при D = AC-B2 > 0 у точці (x0,y0) функція має екстремум (при A<0 – максимум, при A>0 – мінімум ).
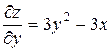
 ,
, ;
;  ;
; 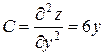 .
. .
. ) , якщо визначники M1>0, M2>0,…, Mn>0, де
) , якщо визначники M1>0, M2>0,…, Mn>0, де ;
; ;
; .
. .
.