 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Линии второго порядка ⇐ ПредыдущаяСтр 4 из 4
15.1.Найти расстояние от центра окружности 15.2.Определить, как расположена прямая 15.3.Привести уравнение к каноническому виду и построить кривую 15.4Найти длину и уравнение перпендикуляра, опущенного из фокуса параболы 15.5Написать уравнение окружности, диаметром которой служит отрезок прямой 15.6Определить, как расположена прямая 15.7Составить уравнение окружности, касающейся двух параллельных прямых 15.8Привести уравнение кривой к каноническому виду и построить её: 15.9Установить тип кривой, её характеристики: центр, вершины, фокусы, эксцентриситет, уравнения директрис: 15.10Определить точки гиперболы 15.11Написать уравнение окружности, проходящей через точку 15.12Привести уравнение к каноническому виду, найти координаты центра, вершин, фокусов, эксцентриситет, уравнения директрис: 15.13Привести уравнение к каноническому виду, найти координаты центра, вершин, фокусов, эксцентриситет, уравнения директрис и асимптот: 15.14Написать уравнение параболы, если известны фокус 15.15Найти угол между радиусами окружности 15.16Привести уравнение кривой 15.17Привести уравнение кривой 15.18На параболе 15.19Найти точки гиперболы 15.20Привести уравнение к каноническому виду, найти координаты центра, вершины, фокуса, уравнение директрисы: 15.21Определить, как расположена прямая 15.22Определить, как расположена прямая 15.23Написать уравнение гиперболы, имеющей вершины в фокусах, а фокусы в вершинах эллипса 15.24Найти точки пересечения асимптот гиперболы
15.25На параболе
15.26На гиперболе
15.27Эллипс, симметричный относительно осей координат, проходит через точки M0(2; 3), B (0;2). Написать его уравнение и найти расстояние точки M от фокусов.
15.28Окружность касается оси Оx в начале координат и проходят через точку A(0;-4). Написать уравнение окружности и найти точки пересечения её с биссектрисами координатных углов. 15.29Через фокус параболы 15.30Написать уравнение окружности, имеющей центр в фокусе параболы
Поиск по сайту: |
 до прямой
до прямой 
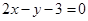 относительно окружности
относительно окружности 
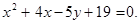
 на прямую, отсекающую на осях координат отрезки
на прямую, отсекающую на осях координат отрезки 
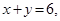 отсеченный гиперболой
отсеченный гиперболой 


 и проходящей через точку
и проходящей через точку 

 Построить кривую.
Построить кривую. расстояние которых до правого фокуса равна
расстояние которых до правого фокуса равна 
 и касающейся осей координат.
и касающейся осей координат. Построить кривую.
Построить кривую. Построить кривую.
Построить кривую. и уравнение директрисы
и уравнение директрисы 
 проведенными в точках пересечения её с осью Oх.
проведенными в точках пересечения её с осью Oх. к каноническому виду, построить её.
к каноническому виду, построить её. к каноническому виду, построить её.
к каноническому виду, построить её. найти точку M0 , ближайшую к прямой
найти точку M0 , ближайшую к прямой 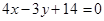 и вычислить расстояние от точки M0 до этой прямой.
и вычислить расстояние от точки M0 до этой прямой. находящиеся на расстоянии 7 от фокуса F1.
находящиеся на расстоянии 7 от фокуса F1.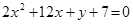 . Построить кривую.
. Построить кривую. относительно эллипса
относительно эллипса 
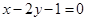 относительно окружности
относительно окружности 

 с окружностью, имеющей центр в правом фокусе гиперболы и проходящей через начало координат.
с окружностью, имеющей центр в правом фокусе гиперболы и проходящей через начало координат. найти точку, фокальный радиус который равен 4,5.
найти точку, фокальный радиус который равен 4,5. взята точка M с ординатой, равной 1. Найти расстояние её от фокусов.
взята точка M с ординатой, равной 1. Найти расстояние её от фокусов. проведена прямая под углом 1200 к оси Oх. Написать уравнение прямой и найти длину образовавшейся хорды.
проведена прямая под углом 1200 к оси Oх. Написать уравнение прямой и найти длину образовавшейся хорды. и касающейся её директрисы. Найти точки пересечения параболы и окружности.
и касающейся её директрисы. Найти точки пересечения параболы и окружности.