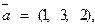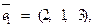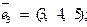|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Скалярное произведение векторовСтр 1 из 4Следующая ⇒
Действия над матрицами Решение матричного уравнения. Матричное уравнение. Решение системы уравнений методом Крамера. Решение системы уравнений методом Гаусса. Решение однородной системы II. Векторная алгебра. стр.18-25 Координаты вектора, базис Скалярное произведение векторов. Векторное произведение векторов. Смешанное произведение векторов. III.Аналитическая геометрия. стр.25-34 Уравнение прямой на плоскости. Уравнение плоскости Уравнения плоскости и прямой в пространстве. Линии второго порядка. IV. Комплексные числа. стр.34-35 Действия с комплексными числами Применение формулы Муавра Решение уравнения с комплексными числами V.Введение в анализ стр.35-44 Пределы Определение точки разрыва функции и исследование характера точек разрыва I. Линейная алгебра 1. Вычислить определитель: а) разложив по элементам і-ой строки; б) разложив по элементам ј–ого столбца; в) приведением к треугольному виду. 1.1.
1.4.
1.7.
1.10.
1.13.
1.16.
1.19.
1.22.
1.25.
1.28.
Выполнить действия над матрицами.
2.1. (А+В) (2Е – А), где
2.2. А – (Е + 2В) B, где
2.3. (А – В) (А +В), где 2.4.(А – В) (А + 2В), где
2.5. (А –В) (2А +Е), где
2.6. (А – В) А + 2Е, где 2.7. (2А - В) А +В, где
2.8. (А – В) А + 3В, где
2.9. 2А + (А + Е) В, где
2.10. 3 (А – В) – 2 АВ, где 2.11. ( 2А – Е) А + 2 В, где
2.12. А ( А - Е ) – (А + В , где
2.13. (А + В) – В (2А + Е), где 2.14. (2Е + В) - В (А – Е), где 2.15. 3 (А + В) (В – Е), где 2.16. 2А – (А + Е) (А –В), где 2.17. 2А + В (А – 2 Е), где
2.18. 2А + В (В – 2А), где 2.19. А – В (А – Е), где
2.20. А – (А + В) (В – 2Е), где
2.21. В (А + 2Е) – 3А, где
2.22. 3 (А + В) – (А – Е) В, где
2.23. (А – В) + 2В (А-Е), где
2.24. (2А + В) В – А, где 2.25. В – 2 (А +Е) В, где 2.26. (А + 2Е) (3Е – В), где 2.27. 2А + А (В – Е), где
2.28. (3А + В) (2В – Е), где 2.29. (2А – В) (В – 2Е), где 2.30. 2А + (А – В) (А – Е), где Решить матричное уравнение.
3.1. 3.2. 3.3. 3.4. 3.6.
3.7. 3.9 .
3.11. 3.12. 3.14. 3.15. 3.16. 3.17. 3.18. 3.19. 3.20 3.21.
3.23. 3.25. 3.26. 3.28.
3.30.
Решить матричное уравнение.
4.1. 4.2. 4.3. 4.4. 4.5. 4.6. 4.7. 4.8. 4.9. 4.10. 4.11. 4.12 . 4.13. 4.14. 4.15. 4.16. 4.17. 4.18. 4.19. 4.20. 4.21. 4.22. 4.23. 4.24. 4.25. 4.26. 4.27. 4.28. 4.29. 4.30.
Решить систему уравнений методом Крамера.
5.1
5.3.
5.5. 5.7.
5.9.
5.11.
5.13.
5.15.
5.17.
5.19.
5.21.
5.23.
5.25.
5.27.
5.29.
Решить систему уравнений методом Гаусса.
6.1. 6.3.
6.5.
6.7.
6.9.
6.11.
6.13.
6.15.
6.17. 6.19. 6.21.
6.23.
6.25.
6.27.
6.29.
7. Найти общее решение однородной системы и записать общее решение через фундаментальную систему решений: 7.1.
7.2. 7.3. 7.4. 7.5. 7.6. 7.7. 7.8. 7.9. 7.10.
7.11. 7.12. 7.13. 9.14. 7.15. 7.16. 7.17. 7.18. 7.19. 7.20. 7.21. 7.22. 7.23.
7.24.
7.25. 7.26. 7.27. 7.28. 7.29. 7.30.
II. Векторная алгебра. 8. Показать, что тройка векторов
8.1.
8.2.
8.3.
8.4.
8.5.
8.6.
8.7.
8.8.
8.9.
Поиск по сайту: |
 1.2.
1.2. 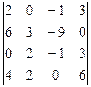 1.3.
1.3. 

 .
.  .
.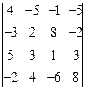 1.5.
1.5.  1.6.
1.6. 
 .
. 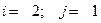

 1.8.
1.8.  1.9.
1.9. 
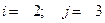 .
.  .
. 
 1. 11.
1. 11.  1.12.
1.12. 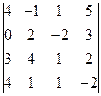
 .
. 

 1.14.
1.14.  1.15.
1.15. 
 .
. 

 1.17.
1.17.  1.18.
1.18. 



 1.20.
1.20.  1.21.
1.21. 
 .
.  .
. 
 1.23.
1.23.  1.24 .
1.24 . 
 .
. 

 1.26.
1.26.  1.27.
1.27. 
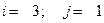
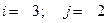

 1.29.
1.29. 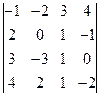 1.30.
1.30. 



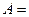
 ,
, 
 .
. ,
,  .
. 
 ,
,  .
. ,
,  .
.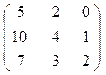 ,
,  .
. ,
,  .
. ,
, 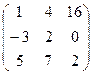 .
. ,
,  .
.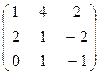 ,
,  .
. ,
, 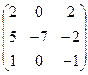 .
.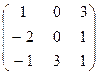 ,
,  .
. ,
,  .
. ,
, 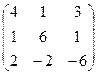 .
. ,
,  .
. .
.  .
.
 .
. ,
,  .
.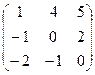 ,
,  .
. ,
,  .
. ,
,  .
.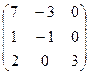 ,
,  .
.
 .
. ,
, 
 .
. ,
, 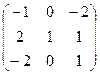 .
. ,
,  .
. ,
,  .
.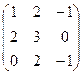 ,
, 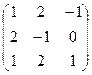 .
. ,
,  .
. ,
,  .
.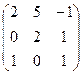 ,
,  .
. *
*  *
* 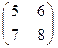
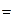
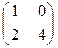 .
. *
* 
 .
.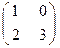

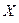
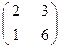
 .
. *
* 
 . 3.5.
. 3.5.  *
*  .
.
 .
.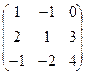 *
*  . 3.8
. 3.8  *
* 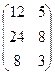 .
. *
*  . 3.10.
. 3.10. 
 .
.
 .
. *
* 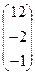 . 3.13.
. 3.13.  *
*  .
.

 .
. *
* 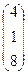 .
.
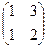
 .
. *
*  .
.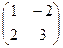

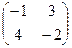 .
. *
*  .
.

 .
. *
*  . 3.22.
. 3.22. 
 .
. *
*  . 3.24.
. 3.24. 
 .
. *
*  . 3.26.
. 3.26.  *
* 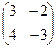
 .
.
 *
*  .
.

 . 3.29.
. 3.29.  *
* 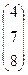 .
.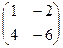
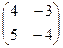 *
*  .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
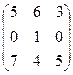



 .
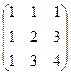
.

 .
.

 .
.
 .
.
 .
.
 .
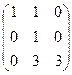
.
 .
.


 .
.
 .
.
 .
.
 .
.
 .
.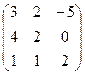
 .
.
 .
. 5.2.
5.2. 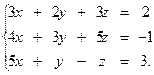
 5.4.
5.4. 
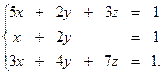 5.6.
5.6. 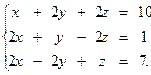
 5.8.
5.8. 
 5.10.
5.10. 
 5.12.
5.12. 
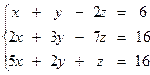 5.14.
5.14. 
 5.16.
5.16. 
 5.18.
5.18. 
 5.20.
5.20. 
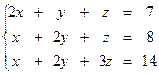 5.22.
5.22. 

 5.24.
5.24. 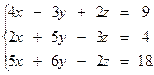
 5.26.
5.26. 
 5.28.
5.28. 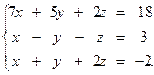
 5.30.
5.30. 
 6.2.
6.2. 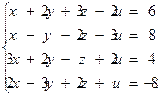
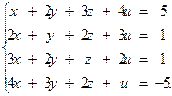 6.4.
6.4. 
 6.6.
6.6. 
 6.8.
6.8. 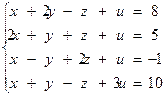
 6.10.
6.10. 
 6.12.
6.12. 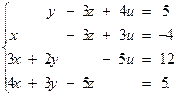
 6.14.
6.14. 
 6. 16.
6. 16. 
 6.18.
6.18. 
 6.20.
6.20. 
 6.22
6.22 
 6.24.
6.24. 
 6.26.
6.26. 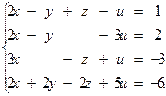
 6.28.
6.28. 
 6.30.
6.30. 






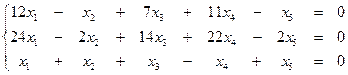


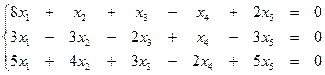




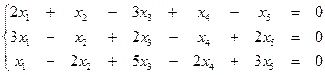









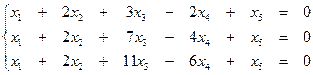
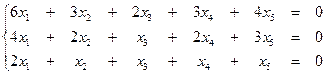

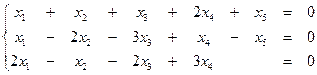
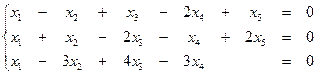

 образует базис. Вычислить координаты вектора
образует базис. Вычислить координаты вектора  в этом базисе.
в этом базисе.
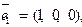 ,
,  ,
, 










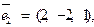
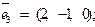





 ,
,  ,
,