 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Техника раскрытий основных видов неопределенностей ⇐ ПредыдущаяСтр 3 из 3
Рассмотрим ситуацию, когда в пределе
возникает неопределенность вида
1. Предположим сначала, что числовые последовательности
В этом случае для раскрытия неопределенности где
Пример 1. Вычислить предел (раскрыть неопределенность
Решение В пределе имеем неопределенность
Выносим за скобки в числителе и знаменателе дроби общий множитель
Учитывая, что последовательности
окончательно получаем
Пример 2. Вычислить предел (раскрыть неопределенность
Решение В пределе имеем неопределенность
Выносим за скобки в числителе и знаменателе дроби общий множитель
Учитывая, как и прежде, что последовательности
окончательно получаем
Вообще, можно доказать, что
2. Предположим теперь, что числовые последовательности Напомним, что факториалом
Замечание. Для определенности считают, что При решении задач будем пользоваться следующим свойством факториала:
Рассмотрим конкретные примеры. Пример 3. Вычислить предел (раскрыть неопределенность
Решение Для раскрытия неопределенности
получим:
Затем вынесем за скобки общий множитель
Пример 4. Вычислить предел (раскрыть неопределенность
Решение Для раскрытия неопределенности
Итак, получаем
Затем выносим за скобки общий множитель
В полученном пределе вновь возникает неопределенность
3. Пусть обе числовые последовательности
Для раскрытия неопределенности рекомендуется в числителе и знаменателе дроби вынести общим множителем показательное выражение где После вынесения выражения Пример 5. Вычислить предел (раскрыть неопределенность
Решение Для раскрытия неопределенности
который является показательным выражением с наибольшим основанием из оснований 2 и 3:
Далее учитываем (см. лекция №2), что числовая последовательность с общим членом
является бесконечно малой последовательностью:
Тогда окончательно получаем
Поиск по сайту: |

 . Метод раскрытие данной ситуации неопределенности непосредственно зависит от того, какой вид имеют общие члены
. Метод раскрытие данной ситуации неопределенности непосредственно зависит от того, какой вид имеют общие члены  числовых последовательностей
числовых последовательностей  . В случае возникновения ситуации неопределенности
. В случае возникновения ситуации неопределенности 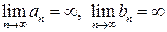 .
. соответственно относительно натуральной переменной
соответственно относительно натуральной переменной  :
:
 необходимо вынести за скобки в числителе и знаменателе дроби общий множитель
необходимо вынести за скобки в числителе и знаменателе дроби общий множитель ,
, – наибольшее из степеней
– наибольшее из степеней  являются бесконечно малыми:
являются бесконечно малыми:  .
.

 (
(  ). Пользуясь теоремами о сходящихся последовательностях, получим
). Пользуясь теоремами о сходящихся последовательностях, получим
 есть бесконечно малые числовые последовательности (
есть бесконечно малые числовые последовательности (  ), а
), а ,
,



 ,
,

 натурального числа
натурального числа  ,
,
 .
. ,
, .
.
 – факториал с наименьшим номером. Используя свойство
– факториал с наименьшим номером. Используя свойство ,
,
 .
.
 – факториал с наименьшим номером. Для этого используем свойства факториала:
– факториал с наименьшим номером. Для этого используем свойства факториала: ,
, .
. .
.
 .
. (см. пункт 1 данного практикума), сокращаем на него и получаем ответ
(см. пункт 1 данного практикума), сокращаем на него и получаем ответ .
. .
. ,
, есть наибольшее из всех оснований показательных выражений.
есть наибольшее из всех оснований показательных выражений. и сокращения на него воспользоваться действиями над сходящимися последовательностями. При этом учесть, что в пределе возникнут бесконечно малые последовательности.
и сокращения на него воспользоваться действиями над сходящимися последовательностями. При этом учесть, что в пределе возникнут бесконечно малые последовательности.
 ,
,

 (
(  ),
), .
.