 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Свойства сходящихся числовых последовательностейСтр 1 из 3Следующая ⇒
ЛЕКЦИИ ПО ДИСЦИПЛИНЕ «Математический анализ» для направления 080100 «Экономика»
Рязань 2012 Тема 1. Числовая последовательность, ее предел
Понятие числовой последовательности. Свойства числовых последовательностей Рассмотрим функцию Определение 1.Функцию, аргументом которой служит натуральное число n, называют числовой последовательностью. Значения функции называются членами или элементами этой последовательности и обозначаются, как правило,
Сокращенно последовательность обозначается символом Суммой, разностью, произведением и частным последовательностей
Символически вышеуказанные действия записываются следующим образом:
Заметим, что значения членов последовательности не должны быть обязательно различными. Например, если
В первом случае имеем просто постоянную величину, во втором члены последовательности принимают два различных значения, в третьем множество значений переменной бесконечно. Определение 2.Последовательность Последовательность называется ограниченной, если она ограничена и снизу, и сверху, то есть существуют такие числа Например, последовательность последовательность последовательность
Предел числовой последовательности, его геометрический смысл. Свойства сходящихся числовых последовательностей Определение 1.Число a называется пределом последовательности
Тот факт, что a является пределом последовательности
Если предел последовательности существует, то говорят также, что последовательность Заметим, что номер N зависит от выбора Используя логические символы, это определение можно записать следующим образом:
Если изобразить числа
Какой бы малый промежуток длины Рассмотрим некоторые свойства сходящихся последовательностей, сформулировав их в виде теорем. Теорема 1. Если последовательность ■ Пусть Теорема 2. Если Для доказательства следует применить предыдущее утверждение, выбрав Теорема 3. Если последовательность ■ Так как Обозначим Теорема 4. Последовательность ■ Предположим, что 3. Бесконечно малые и бесконечно большие последовательности Определение 1.Последовательность Если в определении 1 положить Определение 2.Последовательность ( Пример 1. Последовательность В самом деле, Вернемся к общему случаю существования предела последовательности. Если Обратно, если Теорема 1. Для того, чтобы последовательность Итак, если Бесконечно малым последовательностям противопоставляются в некотором смысле бесконечно большие последовательности. Определение 3.Последовательность Как и в случае бесконечно малых, следует заметить, что ни одно отдельно взятое значение бесконечно большой не может рассматриваться как «большое». Это переменная величина, которая лишь в процессе своего изменения способна сделаться большей произвольно взятого числа M. Пример 2. Последовательность Если последовательность
Если при этом бесконечно большая сохраняет определенный знак, то в соответствии со знаком говорят, что ( Существует связь между бесконечно большими и бесконечно малыми последовательностями, которая устанавливается теоремой 6. Теорема 2. 1) Если 2) если ■ Выберем любое число Символически утверждение теоремы запишем так:
Пример 3.
Поиск по сайту: |
 , где
, где 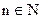 .
.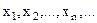 , так что
, так что 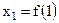 ,
,  ,…,
,…, 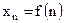 .
. . Геометрически последовательность изображается на координатной прямой в виде последовательности точек, координаты которых равны соответствующим элементам последовательности.
. Геометрически последовательность изображается на координатной прямой в виде последовательности точек, координаты которых равны соответствующим элементам последовательности.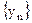 называются соответственно последовательности
называются соответственно последовательности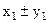 ,
,  , …,
, …,  ,…,
,…,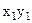 ,
,  , …,
, …,  ,…,
,…, ,
, 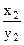 , …,
, …, 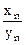 , …
, … 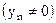 .
.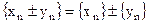 ,
,  ,
, 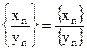 .
.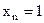 ,
, 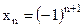 ,
,  , то соответствующие последовательности имеют вид
, то соответствующие последовательности имеют вид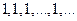 ;
;  ;
; 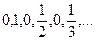 .
.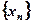 назовем ограниченной сверху (снизу), если существует такое число
назовем ограниченной сверху (снизу), если существует такое число 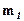 (
( 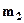 ), что любой элемент этой последовательности удовлетворяет неравенству
), что любой элемент этой последовательности удовлетворяет неравенству 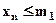 (
(  ).
). и
и 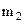 , что для любого
, что для любого  :
:  . Обозначим
. Обозначим 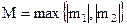 . Тогда условие ограниченности можно записать в виде
. Тогда условие ограниченности можно записать в виде  .
.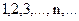 ограничена снизу, но не ограничена сверху;
ограничена снизу, но не ограничена сверху;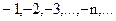 ограничена сверху, но не ограничена снизу;
ограничена сверху, но не ограничена снизу;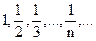 ограничена, так как любой элемент
ограничена, так как любой элемент 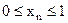 .
.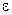 , сколь бы мало оно ни было, существует такой номер
, сколь бы мало оно ни было, существует такой номер  , что для всех
, что для всех 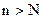 выполняется неравенство
выполняется неравенство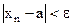 . (2.1)
. (2.1)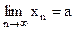 или
или 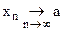 . (2.2)
. (2.2)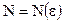 .
.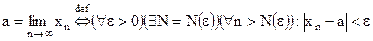 .
.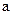 ,
, 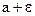 ,
, 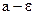 и значения
и значения 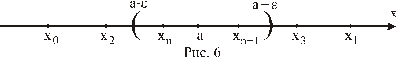
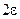 с центром в точке a ни взять, все точки
с центром в точке a ни взять, все точки  , который рассмотрим позднее.
, который рассмотрим позднее.
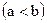 , то и члены последовательности
, то и члены последовательности 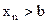
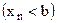 , начиная с некоторого номера.
, начиная с некоторого номера.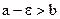 ; для этого достаточно взять
; для этого достаточно взять 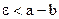 . Но тогда по определению предела найдется такой номер N, что для
. Но тогда по определению предела найдется такой номер N, что для 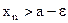 , а, следовательно, тем более
, а, следовательно, тем более 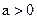
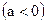 , то и
, то и 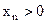
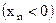 , начиная с некоторого номера.
, начиная с некоторого номера.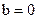 .
. . Но
. Но 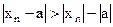 , следовательно,
, следовательно, 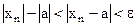 ; откуда
; откуда 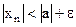 для
для 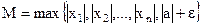 . Тогда для всех n
. Тогда для всех n  и
и  , причем
, причем  . Выберем любое число
. Выберем любое число 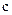 ,
, 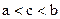 . Так как
. Так как 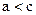 , то существует такой номер
, то существует такой номер 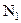 , что для
, что для 
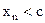 (на основании теоремы 1). С другой стороны, так как
(на основании теоремы 1). С другой стороны, так как 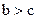 , то существует такой номер
, то существует такой номер 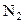 , что для
, что для 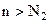
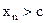 . Тогда для N, большего
. Тогда для N, большего 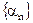 называется бесконечно малой, если
называется бесконечно малой, если 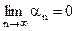 .
.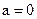 , то неравенство (2.1) примет вид
, то неравенство (2.1) примет вид  . Следовательно, определение бесконечно малой последовательности может быть сформулировано следующим образом.
. Следовательно, определение бесконечно малой последовательности может быть сформулировано следующим образом.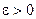 существует такой номер N, что для
существует такой номер N, что для 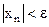 .
.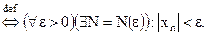 )
)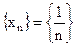 является бесконечно малой.
является бесконечно малой.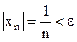 лишь только
лишь только  . Следовательно, в качестве
. Следовательно, в качестве  можно взять целую часть числа
можно взять целую часть числа 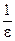 . Заметим, что ни одно отдельно взятое значение бесконечно малой последовательности (если оно не нуль) не может рассматриваться как «малое». Дело в том, что это переменная величина, которая лишь в процессе своего изменения способна сделаться меньшей произвольно выбранного числа
. Заметим, что ни одно отдельно взятое значение бесконечно малой последовательности (если оно не нуль) не может рассматриваться как «малое». Дело в том, что это переменная величина, которая лишь в процессе своего изменения способна сделаться меньшей произвольно выбранного числа 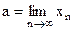 , то разность
, то разность 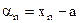 будет бесконечно малой, так как в силу (1)
будет бесконечно малой, так как в силу (1)  при
при 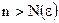 .
.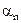 – бесконечно малая, то
– бесконечно малая, то 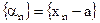 была бесконечно малой.
была бесконечно малой.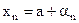 , где
, где 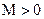 существует такой номер
существует такой номер 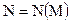 , что
, что  для всех номеров
для всех номеров 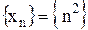 является бесконечно большой, так как
является бесконечно большой, так как 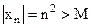 , лишь только
, лишь только 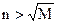 . Следовательно, в качестве
. Следовательно, в качестве 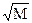 .
.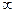 или стремится к
или стремится к  (
(  ).
). или
или 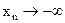 (
(  либо
либо 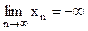 ).
). .)
.)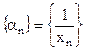 – бесконечно малая последовательность;
– бесконечно малая последовательность;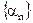 (
( 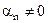 ) – бесконечно малая, то
) – бесконечно малая, то 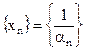 – бесконечно большая последовательность.
– бесконечно большая последовательность. , то для числа
, то для числа 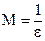 найдется такой номер N, что
найдется такой номер N, что 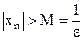 , как только
, как только 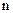
 , что и доказывает утверждение. Аналогично доказывается и вторая часть утверждения. ■
, что и доказывает утверждение. Аналогично доказывается и вторая часть утверждения. ■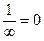 ,
, 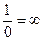 .
.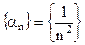 – бесконечно малая последовательность, а
– бесконечно малая последовательность, а  – бесконечно большая.
– бесконечно большая.