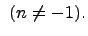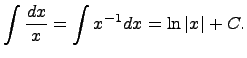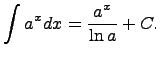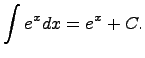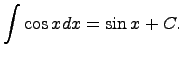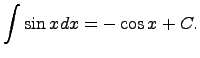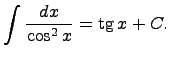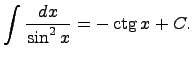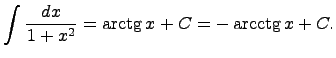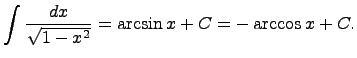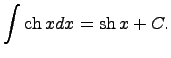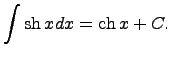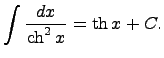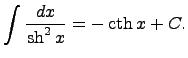|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Возрастание и убывание функции ⇐ ПредыдущаяСтр 2 из 2
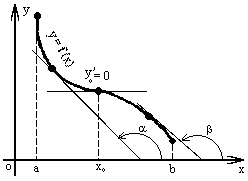
Функция f(x) называется возрастающей в интервале (a,b), если при возрастании аргумента x в этом интервале соответствующие значения функции f(x) также возрастают, т.е. если
f(x2) > f(x1) при x2 > x1.
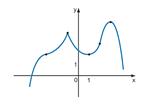
Функция f (x) называется убывающей в интервале ( a, b ) если при возрастании аргумента x в этом интервале соответствующие значения функции f (x) убывают, т.е. если f(x2) < f(x1) при x2 > x1. Из этого определения следует, что у убывающей в интервале ( a, b ) функции f (x) в любой точке этого интервала приращения Dx и Dy имеют разные знаки. Экстремумы функций Слово «экстремум» значит крайний. Точкой экстремума называется такая точка, в которой функция принимает крайние значения: наибольшее или наименьшее. Критической точкой функции называется такая точка ее области определения, в которой производная функции обращается в нуль или не существует. Критические точки функции, в которых она меняет возрастание на убывание или убывание на возрастание, называются точками экстремума. Если в точке экстремума функция меняет убывание на возрастание, то в этой точке достигается наименьшее значение хотя бы на небольшом участке ее области определения. Говорят, что такая точка является точкой локального минимума. Если в точке экстремума функция меняет возрастание на убывание, то в этой точке достигается наибольшее значение хотя бы на небольшом участке ее области определения. Говорят, что такая точка является точкой локального максимума.
Асимптота Определение (основное). Прямая называется асимптотой к кривой, если точка этой кривой неограниченно приближается к асимптоте при удалении точки по кривой в бесконечность. Определение. Если для функции
тогда прямая
называется вертикальной асимптотой к функции Определение. Если существуют конечные пределы:
то прямая
называется горизонтальной асимптотой к функции Определение. Если существуют конечные пределы:
и
тогда у функции
18)первообразные и неопределенные интегралы Неопределенным интегралом Задача нахождения неопределенного интеграла заключается в нахождении такой функции,производная которой равняется подынтегральному выражению. Данная функция определяется с точностью до постоянной, т.к. производная от постоянной равняется нулю. Например, известно, что
Пусть функция
то функция интегрирования – операции, обратной дифференцированию. 19)таблица интегралов 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. Здесь C - произвольная постоянная, т.к. производная от постоянной есть нуль, следовательно, неопределённый определяется с точностью до постоянной.
| ||
Поиск по сайту:

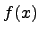 выполняется, что
выполняется, что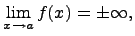
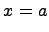
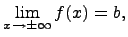
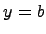
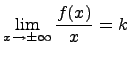
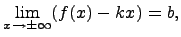
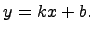
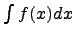 называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равенподынтегральному выражению f(x)dx, т.е.
называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равенподынтегральному выражению f(x)dx, т.е.  или
или  Функцию
Функцию 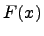 называют первообразной функции
называют первообразной функции 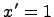 , тогда получается, что
, тогда получается, что 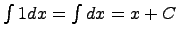 , здесь
, здесь  - произвольная постоянная.
- произвольная постоянная. задана на некотором интервале
задана на некотором интервале  . Если найдётся такая функция
. Если найдётся такая функция 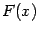 , что при всех
, что при всех 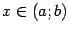 имеет место равенство
имеет место равенство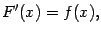
 где
где