 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Производная сложной и обратной функцииСтр 1 из 2Следующая ⇒
Теорема
4)Предел функции Пусть функция f (x) определена на некотором открытом интервале [b,c], содержащим точку x = a. (При этом не требуется, чтобы значение f (a) было обязательно определено.) Число A называется пределом функции f (x) при
при условии
Данное определение предела известно как Существует также определение предела функции по Гейне, согласно которому функция f (x)имеет предел A в точке x = a, если для каждой последовательности
5)Число е ,замечательный предел Числом e называется предел
Это число иррациональное и приближенно равно е = 2.718281828.... Логарифмы с основанием е называются натуральными и обозначаются
Данный предел называют вторым замечательным пределом. Многие примеры сводятся с помощью простых хамен ко второму замечательному пределу. Рассмотрим несколько примеров решения на второй замечательный предел. Пример 1 - найти предел используя второй замечательный предел Найти предел:
Решение. Преобразуем предел:
Используя свойства пределов , а конкретно, что если функция
Замечаем, что можно применить второй замечательный предел и получаем ответ.
Исходный предел равен:
6)
при этом предел знаменателя
8)Непрерывность функции, разрывы Пусть функция f(x) определена на некотором множестве Е и х0 – предельная точка множества Е. Функция f(x) называется непрерывной в точке х0, если 1. Она определена в точке х0 Существует конечный предел
3. Этот предел равен значению функции в точке х0. Иначе говоря, функция у=f(x) называется непрерывной в точке, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть
Разрывность функции Итак, если хотя бы одно из трех условий непрерывности не выполняется, функция называется разрывной в точке х0, а сама точка x0-точкой разрыва. Если в точке x0 оба односторонних предела существуют и конечны, то разрыв называется разрывом первого рода. Пусть х0-точка разрыва первого рода, т.е. Возможны два случая 1. f(x0+0)=f(x0-0)=L, но либо функция f(x) не определена в точке х0, либо f(x0) # L (то есть не выполнено либо первое либо третье условие непрерывности). В этом случае разрыв называется устранимым, так как если доопределить функцию в точке х0 или переопределить ее, положив f(x0)=L, функция f(x) станет непрерывной в точке х0.
2. f(x0- 0) ¹ f(x0+0) B этом случае разрыв называется неустранимым. Если же хотя бы один из односторонних пределов f(x0+0) или f(x0-0) не существует или бесконечен, то разрыв называется разрывом второго рода. Разрыв второго рода всегда неустранимый. Если в точке х0 функции f(x) и g(x) непрерывны, то в этой же точке непрерывными являются и функции
9)Производная ,геом смысл Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.
Если функция
Функция fl называется касательной к f в точке x0. Число Дифференциал Дифференциал+ (от лат. differentia — разность, различие) — линейная часть приращения функции. Обычно дифференциал функции f обозначается df. Для функций Дифференциал функции
где f'(x0) обозначает производную f в точке x0. Таким образом df есть функция двух аргументов Дифференциал может быть определён напрямую, т.е., без привлечения определения производной как функция
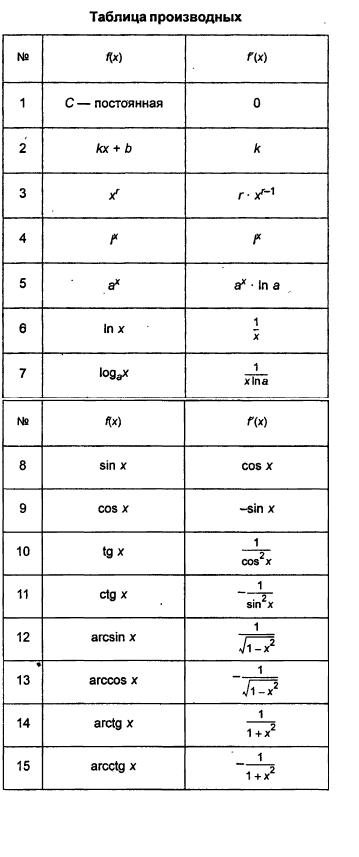
Таблица производных
Доказательство y = xn. Если n – целое положительное число, то, используя формулу бинома Ньютона: (a + b)n = an+n·an-1·b + 1/2∙n(n – 1)an-2∙b2+ 1/(2∙3)∙n(n – 1)(n – 2)an-3b3+…+ bn, Можно доказать, что
Итак, если x получает приращение Δx, то f(x+Δx) = (x + Δx)n, и, следовательно, Δy=(x+Δx)n – xn =n·xn-1·Δx + 1/2·n·(n–1)·xn-2·Δx2 +…+Δxn. Заметим, что в каждом из пропущенных слагаемых есть множитель Δx в степени выше 3. Найдем предел
Производная сложной и обратной функции
Правило Лопиталя Пусть при x
Эта теорема называется правилом Лопиталя. Она позволяет вычислять пределы отношения функций, когда и числитель, и знаменатель cтремятсялибо к нулю, либо к бесконечности. Правило Лопиталя, как говорят математики, позволяет избавляться от неопределённостей типа: 0 / 0 и
Поиск по сайту: |
 при
при 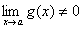
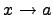 , если для любого
, если для любого  существует такое
существует такое  , что выполняется
, что выполняется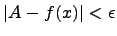
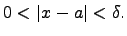
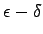 - определение или определение Коши.
- определение или определение Коши.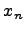 , сходящейся к точке a, последовательность
, сходящейся к точке a, последовательность 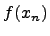 сходится к A.
сходится к A.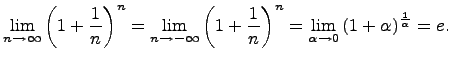
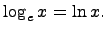
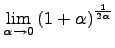

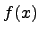 непрерывна в точке a, то
непрерывна в точке a, то 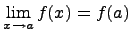 , получим:
, получим: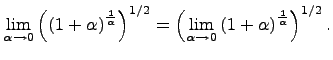
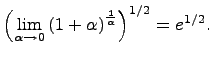
 .
.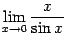 .
.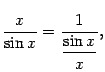
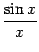 -- это первый замечательный предел, равный 1 (и, следовательно, не равный 0). Числитель правой части, равный 1, имеет предел 1. Значит, по теореме о пределе отношения,
-- это первый замечательный предел, равный 1 (и, следовательно, не равный 0). Числитель правой части, равный 1, имеет предел 1. Значит, по теореме о пределе отношения,

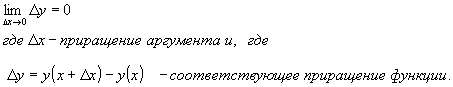
 оба односторонних предела существуют, конечны и равны.
оба односторонних предела существуют, конечны и равны.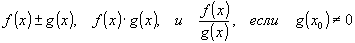
 имеет конечную производную в точке x0, то в окрестности U(x0) её можно приблизить линейной функцией
имеет конечную производную в точке x0, то в окрестности U(x0) её можно приблизить линейной функцией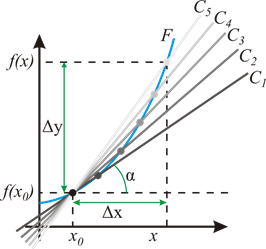
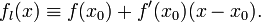
 является угловым коэффициентом или тангенсом угла наклонакасательной прямой.
является угловым коэффициентом или тангенсом угла наклонакасательной прямой. в точке
в точке 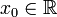 может быть определён как линейная функция
может быть определён как линейная функция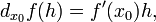
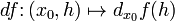 .
.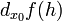 линейно зависящая от h и для которой верно следующее соотношение
линейно зависящая от h и для которой верно следующее соотношение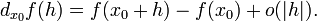
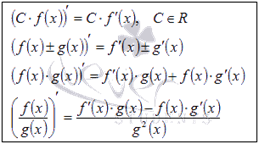

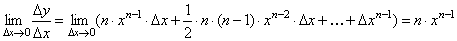
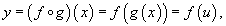 где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция
где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция 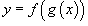 также дифференцируема по x и ее производная равна
также дифференцируема по x и ее производная равна
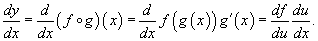 Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную
от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции
- в точке u = g(x)!
Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную
от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции
- в точке u = g(x)!
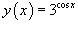 .
Решение.
Поскольку
.
Решение.
Поскольку 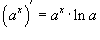 , то по правилу производной сложной функции получаем
, то по правилу производной сложной функции получаем
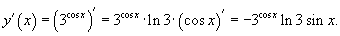 Обратная
Рассмотрим функцию y = f(x), для которой существует обратная функция x = g(y).
Теорема 5. Если обратная функция x = g(y) дифференцируема и g'(y) ≠ 0, то функцияy=f(x) дифференцируема, и
Обратная
Рассмотрим функцию y = f(x), для которой существует обратная функция x = g(y).
Теорема 5. Если обратная функция x = g(y) дифференцируема и g'(y) ≠ 0, то функцияy=f(x) дифференцируема, и 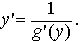 Доказательство
Если аргумент x получит приращение Δx, то функция f получит приращение
Δy = f(x + Δx) − f(x).
С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом:
Δx=g(y + Δy) − g(y).
Тогда получаем
Доказательство
Если аргумент x получит приращение Δx, то функция f получит приращение
Δy = f(x + Δx) − f(x).
С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом:
Δx=g(y + Δy) − g(y).
Тогда получаем
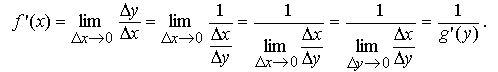 13)Теоремы
Теорема 1. Теорема Ро́лля утверждает, что если функция, имеющая производную на интервале, принимает в его концах равные значения, то её производная обращается в нуль в некоторой точке внутри интервала.
(Теорема Ролля) Пусть функция f(x)
1. непрерывна на отрезке [a, b];
2. дифференцируема в интервале (a, b);
3. на концах отрезка [a, b] принимает равные значения.
Тогда существует точка c Î (a, b) такая, что f'(c) = 0.
Теорема 2. (Теорема Лагранжа) Пусть функция f(x)
1. непрерывна на отрезке [a, b];
2. дифференцируема в интервале (a, b).
Тогда существует точка с Î (a, b) такая, что
13)Теоремы
Теорема 1. Теорема Ро́лля утверждает, что если функция, имеющая производную на интервале, принимает в его концах равные значения, то её производная обращается в нуль в некоторой точке внутри интервала.
(Теорема Ролля) Пусть функция f(x)
1. непрерывна на отрезке [a, b];
2. дифференцируема в интервале (a, b);
3. на концах отрезка [a, b] принимает равные значения.
Тогда существует точка c Î (a, b) такая, что f'(c) = 0.
Теорема 2. (Теорема Лагранжа) Пусть функция f(x)
1. непрерывна на отрезке [a, b];
2. дифференцируема в интервале (a, b).
Тогда существует точка с Î (a, b) такая, что
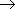 a для функций f ( x ) и g ( x ), дифференцируемых в некоторой окрестности точки а , выполняются условия:
a для функций f ( x ) и g ( x ), дифференцируемых в некоторой окрестности точки а , выполняются условия:
 /
/