 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Предел функции в точке ⇐ ПредыдущаяСтр 2 из 2
Пусть функция y=f(x) задана в некоторой окрестности точки x0, кроме быть может, самой точки x0. Определение. Число А называется пределом функции f(x) при x®x0, если, для любого сколь угодно малого положительного числа e>0 найдется такое положительное число d>0 (зависящее от e), что для всех x, не равных x0 и удовлетворяющих неравенству Этот предел обозначается Если последовательность {f(xn)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу x0, то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:
Переменная величина (т.е. последовательность или функция), имеющая своим пределом нуль, называется бесконечно малой величиной. Переменная величина, имеющая бесконечный предел, называется бесконечно большой величиной. Для нахождения пределов на практике пользуются следующими теоремами. Теорема 1. Если существуют пределы
Замечание. Выражения вида 0/0, ¥ /¥, 0 × ¥, ¥ - ¥ являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и нахождение пределов такого вида носит название “раскрытие неопределенностей”. Теорема 2.
Замечательные пределы Первым замечательным пределом называется
Вторым замечательным пределом называется
где e » 2.718281…- число Эйлера. На практике также используются формулы для пределов последовательности: Используются на практике и формулы вида:
Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины. К таким задачам, например, относятся: рост вклада по закону сложных процентов, рост населения страны, распад радиоактивного вещества, размножение бактерий и т.п. Рассмотрим пример Я. И. Перельмана, дающий интерпретацию числа e в задаче о сложных процентах. В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример. Пусть в банк положено 100 ден. ед. из расчета 100% годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 × 1,5 = 150, а еще через полгода - в 150 × 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100×(1+1/3)3»237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится: 100 × (1 +1/10)10 » 259 (ден. ед.), 100 × (1+1/100)100 » 270 (ден. ед.), 100 × (1+1/1000)1000 » 271 (ден. ед.). При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что
Пример. Найти предел последовательности, заданной общим членом Решение. Применим теорему о пределе суммы и найдем предел каждого слагаемого. При n ®¥ числитель и знаменатель каждого слагаемого стремится к бесконечности, и мы не можем непосредственно применить теорему о пределе частного. Поэтому сначала преобразуем xn, разделив числитель и знаменатель первого слагаемого на n2, а второго на n. Затем, применяя теорему о пределе частного и о пределе суммы, найдем: Пример. Решение. Здесь мы воспользовались теоремой о пределе степени: предел степени равен степени от предела основания. Пример. Найти ( Решение. Применять теорему о пределе разности нельзя, поскольку имеем неопределенность вида ¥ - ¥. Преобразуем формулу общего члена: Пример. Найти Решение. Имеем: Пример. Вычислить Решение. Обозначим y=p-x. Тогда при x®p, y®0.Имеем: sin 3x = sin 3(p-y) = sin (3p-3y) = sin 3y и sin 4x = sin 4(p-y) = sin (4p-4y)= - sin 4y. Пример. Найти Решение. Обозначим arcsin x=t. Тогда x=sint и при x®0 t®0. Пример. Найти 1) Решение. 1. Применяя теорему 1 о пределе разности и произведения, находим предел знаменателя: Предел знаменателя не равен нулю, поэтому, по теореме 1 о пределе частного, получаем: 2. Здесь числитель и знаменатель стремятся к нулю, т.е. имеет место неопределенность вида 0/0. Теорема о пределе частного непосредственно неприменима. Для “раскрытия неопределенности” преобразуем данную функцию. Разделив числитель и знаменатель на x-2, получим при x ¹ 2 равенство: Так как 3. Числитель и знаменатель при x®¥ являются бесконечно большими функциями. Поэтому теорема о пределе частного непосредственно не применима. Разделим числитель и знаменатель на x2 и к полученной функции применим теорему о пределе частного: Пример. Найти Решение. Здесь числитель и знаменатель стремятся к нулю: Преобразуем данную функцию, умножив числитель и знаменатель на неполный квадрат суммы выражения Пример. Найти Решение.
Поиск по сайту: |
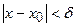 , выполняется неравенство êf(x)-A ê < e.
, выполняется неравенство êf(x)-A ê < e.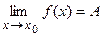 .
. или
или 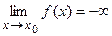 .
.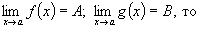


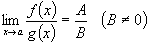 .
.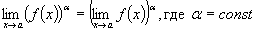 , т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности
, т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности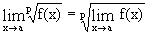 ;
;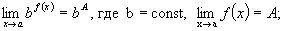
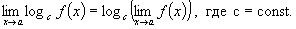 .
.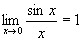 .
. его можно записать в другом виде:
его можно записать в другом виде:  ,
,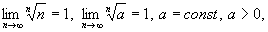
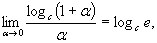

 , в частности,
, в частности, 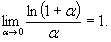
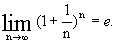
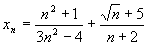 .
. .
. . Найти
. Найти  .
. .
. ).
). .
.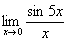 .
.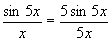 . Обозначим t = 5x. При x®0 имеем: t®0. Применяя формулу первого замечательного предела, получим
. Обозначим t = 5x. При x®0 имеем: t®0. Применяя формулу первого замечательного предела, получим 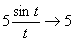 .
.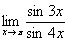 .
.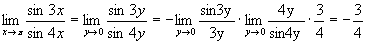 .
.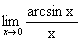 .
.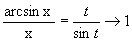 .
.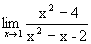 ; 2)
; 2) 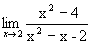 ; 3)
; 3) 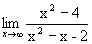 .
.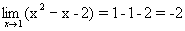 .
.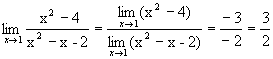 .
.
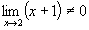 , то по теореме о пределе частного найдем
, то по теореме о пределе частного найдем
 .
.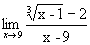 .
. , x-9®0, т.е. имеем неопределенность вида
, x-9®0, т.е. имеем неопределенность вида 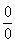 .
.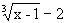 , получим
, получим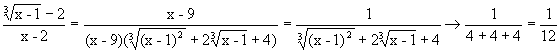 .
. .
.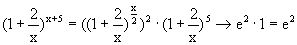 .
.