 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Предел функции в бесконечностиСтр 1 из 2Следующая ⇒
Пределы и непрерывность Предел числовой последовательности Определение. Если по некоторому закону каждому натуральному числу n поставлено в соответствие определенное число an, то говорят, что задана числовая последовательность {an}:
Другими словами, числовая последовательность – это функция натурального аргумента: Числа Примеры: 2,4,6,8,…,2n,…- монотонная, неограниченная. 1,0,1,0,… - немонотонная, ограниченная.
Можно заметить, что члены последовательности с ростом n сколь угодно близко приближаются к 1. При этом абсолютная величина разности
то есть с ростом n величина Определение. Число А называется пределом числовой последовательности {an}, если для любого сколь угодно малого положительного числа
Записывают это следующим образом: Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся. Геометрический смысл предела числовой последовательности состоит в том, что точки an, начиная с некоторого номера n>N, лежат внутри интервала (A-e, A+e), т.е. попадают в какую угодно малую e-окрестность точки а.
Предел функции в бесконечности Понятие предела функции является обобщением понятия предела последовательности, так как предел последовательности можно рассматривать как предел функции xn = f(n) целочисленного аргумента n. Пусть дана функция f(x) и пусть A - предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от A. Точка A может принадлежать множеству D(f), а может и не принадлежать ему. Определение. Число А называется пределом функции y=f(x) при x®¥, если для любого сколь угодно малого положительного числа e>0 найдется такое положительное число S>0 (зависящее от e), что для всех x, таких, что
Этот предел обозначается Геометрический смысл: неравенство
Поиск по сайту: |
 .
.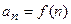 .
. называются членами последовательности, а число an – общим членом данной последовательности.
называются членами последовательности, а число an – общим членом данной последовательности. - немонотонная, ограниченная. Рассмотрим эту последовательность подробнее. Изобразим ее члены точками числовой оси.
- немонотонная, ограниченная. Рассмотрим эту последовательность подробнее. Изобразим ее члены точками числовой оси.
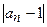 становится все меньше и меньше:
становится все меньше и меньше: ,
,  ,
,  ,
,  ,…,
,…,  ,…,
,…,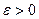 найдется такой номер N (зависящий от e), что для всех членов последовательности с номерами n>N верно неравенство
найдется такой номер N (зависящий от e), что для всех членов последовательности с номерами n>N верно неравенство .
.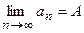 или an ® A при n®¥.
или an ® A при n®¥. , верно неравенство
, верно неравенство .
. .
.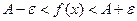 , соответствующему расположению части графика в полосе шириной 2e.
, соответствующему расположению части графика в полосе шириной 2e.