 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ОБЩИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ⇐ ПредыдущаяСтр 2 из 2
Понятие о дифференциальных уравнениях. Дифференциальные уравнения используются при изучении явлений и процессов в физике, химии, биологии, медицине, фармации, астрофизике, кибернетике, социологии и других областях знаний. Сформулировав задачу на языке дифференциальных уравнений, специалист любой отрасли знаний получает в руки готовый аппарат для численного решения задачи, изучения качественных особенностей этого решения. Многие вопросы естествознания и техники сводятся к нахождению неизвестной функции у = f(x), если известно уравнение, содержащее х, у и производные разных порядков функции f(x): f¢(x), f¢¢(x), …, f(n)(x) или дифференциалы функции df, d2f, …, dnf. Такие уравнения называются дифференциальными. Рассмотрим задачу, приводящую к дифференциальному уравнению: установить закон изменения скорости u свободно падающего тела массой т без учета силы сопротивления воздуха. Согласно второму закону Ньютона,
где mg – сила тяжести. Полученное уравнение является дифференциальным, так как в него входит производная du/dt искомой функции u. Решить дифференциальное уравнение – значит найти такую функцию u = f(t) , которая тождественно удовлетворяет этому уравнению. Легко проверить, что уравнению удовлетворяет функция вида u = gt + C, где С – любое число. Указав начальные условия, можно найти одну функцию, удовлетворяющую уравнению. Так, если при t = 0 u = u0, то получим функцию u = u0 + gt. Существует много задач из различных областей знаний, решение которых сводится к составлению и решению дифференциальных уравнений. Основные определения теории обыкновенных дифференциальных уравнений. Дифференциальным называют уравнение, связывающее аргумент х, искомую функцию у = f(x), ее производные f¢(x), f¢¢(x), …, f(п)(x) или дифференциалы df, d2f, …, dпf. Дифференциальное уравнение в общем виде можно записать так: F(x, f(x), f¢(x), f¢¢(x), …, f(п)(x)) = 0 или F(x, y, y¢, y¢¢, …, y(n)) = 0. Если искомая функция y = f(x) есть функция одного аргумента, то дифференциальное уравнение называют обыкновенным. Если функция u = f(x, y, z, …, t) зависит от двух и большего числа аргументов, то уравнение будет содержать частные производные Порядком дифференциального уравнения называется порядок наивысшей производной или дифференциала, входящих в уравнение. Например, у¢ = 2ху2 + 5 – уравнение первого порядка, а у¢¢ + у =0 – второго. Общим решением дифференциального уравнения порядка r называется функция y = f(x,C1, C2, …, Cr) от х с произвольными постоянными C1, C2, …, Cr,обращающая это уравнение в тождество. Общее решение, записанное в неявном виде Ф(x, у,C1, …, Cr) = 0, называется общим интегралом. Так, решением дифференциального уравнения у¢¢ + у =0 является функция у = С1 sin x + C2 cos x, где C1 и C2 – произвольные постоянные. При подстановке функции у = С1 sin x + C2 cos x в уравнение у¢¢ + у =0 оно превращается в тождество. Действительно, у¢х = C1 cos x – С2 sin x; у¢¢хх = - С1 sin x - C2 cos x; - С1 sin x - C2 cos x + С1 sin x + C2 cos x =0. При любом наборе конкретных постоянных получаются частные решения. На практике частное решение получают из общего не прямым заданием значений произвольных постоянных, а с учетом тех условий, которым должно удовлетворять искомое частное решение. Задание таких условий называется заданием начальных условий и записывается кратко так: f(x0) = y0; f¢(x0) = y¢0;…; f(r-1)(x0) = y0(r-1). Задача нахождения частного решения, удовлетворяющего начальным условиям, называется задачей Коши. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА Уравнение вида f1(x)j1(y)dx + f2(x)j2(y)dy =0 называется уравнением с разделяющимися переменными. Оно может быть приведено к уравнению с разделенными переменными путем деления обеих его частей на j1(y) f2(x):
при условии, что j1(y) f2(x) ¹ 0. После сокращения получаем
Интегрируя равенство (1), получаем
где С – произвольная постоянная. Выражение (2) является общим решением уравнения (1). Пример. Найти общее и частное решения уравнения dy/dx = - y/x при x = 1, y = 2. Решение. В уравнении dy/dx = - y/x путем умножения обеих частей на dx разделим (отделим) дифференциалы: dy = -( y/x)dx. Разделив обе части последнего уравнения на у, получим уравнение с разделенными переменными: dy/у = -dx/x. Проинтегрируем его:
Потенцируя последнее равенство, получаем
Однородные дифференциальные уравнения первого порядка. Уравнение dy/dx = f(x,y) называется однородным уравнением первого порядка, если функция f(x,y) может быть представлена как функция отношения своих аргументов: f( x, y)= j(y/x). Например, уравнение dy/dx = ху/(х2 – у2) однородное, так как, разделив числитель и знаменатель правой части на х2 , получим
Поиск по сайту: |

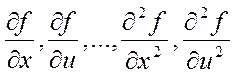 и т.д. Такое уравнение носит название дифференциального уравнения в частных производных. Мы будем рассматривать только обыкновенные дифференциальные уравнения.
и т.д. Такое уравнение носит название дифференциального уравнения в частных производных. Мы будем рассматривать только обыкновенные дифференциальные уравнения.
 (1)
(1) (2)
(2)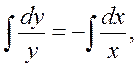 откуда
откуда
 - общее решение уравнения.Из условия, что при х = 1 у = 2, найдем значение С: 2 = С/1, откуда С = 2. Частное решение будет иметь вид у = 2/х.
- общее решение уравнения.Из условия, что при х = 1 у = 2, найдем значение С: 2 = С/1, откуда С = 2. Частное решение будет иметь вид у = 2/х.