 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
КОНТРОЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ №2 ⇐ ПредыдущаяСтр 2 из 2
I. Найти пределы функции.
II. Найти точки разрыва функции
ОБРАЗЕЦ ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ №3 «Производная и ее приложение к исследованию функции»
Вариант 0 I. Найти
II. Найти III. Найти IV. Найти V. Исследовать и построить график функции
VI. Найти наибольшее и наименьшее значение функции
VII. Составить уравнения касательных к линии
I. Решение. 1.
2.
3.
4.
5.
6.
7.
II. Найти
III. Найти
IV. Найти
V. Исследовать и построить график функции
1. Функция определена всюду, т.е. область определения (-∞;+∞) 2. Функция общего вида 3. Вертикальные асимптоты. Т.к. нет особенностей в области определения, то функция вертикальных асимптот не имеет. 4. Асимптоты 5. Интервалы монотонности и точки экстремумов.
а). Найдем производную:
в).
6. Интервалы выпуклости вогнутости, точки перегиба.
а). Найдем
б). Найдем критические точки 2-го рода:
в).
В точке
7. Точки пересечения с осью
Точка пересечения с осью
 . .
Из графика видно, что функция 3 раза пересекает ось Х.
2). 1. Функция определена всюду, кроме точки 2. Функция общего вида. 3. Функция непрерывна на своей области определения. Исследуем функцию в точке
Эти пределы различны и бесконечны, т.е. в точке 4. Так как функция имеет в точке
График имеет асимптоту 5. Найдем производную функции:
 . Выясним, при каких значениях . Выясним, при каких значениях 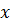 производная равна нулю. Решим уравнение производная равна нулю. Решим уравнение  . Вычисляя дискриминант, получаем . Вычисляя дискриминант, получаем  , поэтому корней у этого уравнения нет , поэтому корней у этого уравнения нет
Производная всюду положительна, экстремумов у графика функции нет, функция возрастает на интервалах
1. Найдем вторую производную функции:
Вторая производная нигде не обращается в нуль, поэтому функция не имеет точек перегиба.
При 7. Найдем точки пересечения графика функции с осями координат. Имеем
 , поэтому с осью , поэтому с осью 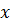 функция пересекается в точках функция пересекается в точках 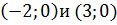
VI. 1. Найдем
2. Найдем критические точки
функция, поэтому ее рассматривать не нужно. 3. Посмотрим, все ли критические точки лежат в рассматриваемом интервале:
4. Найдем значение в оставшейся критической точке
5. Из получившихся значений выбираем самое большое и самое маленькое
VII. 1. Найдем точки пересечения
2. Т.к. уравнение касательной в точке
то вычислим
Имеем две касательные с уравнениям
Поиск по сайту: |

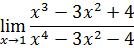






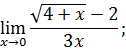













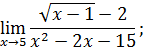













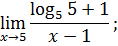
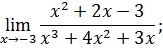






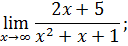



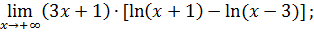

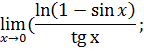




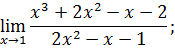

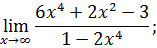




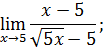

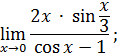
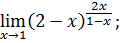
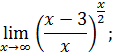
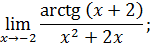


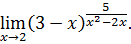
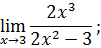
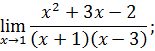









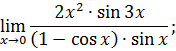


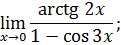








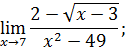
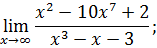
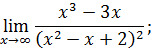




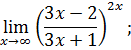



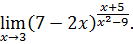





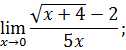




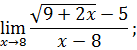
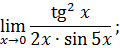


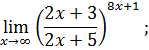

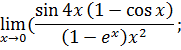




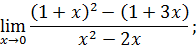


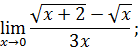

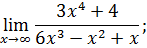




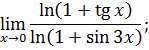










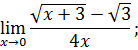




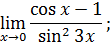





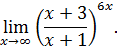
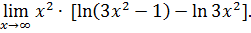
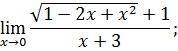
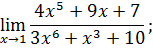






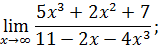



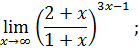






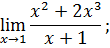


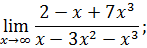
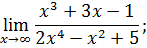




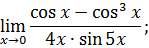





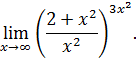


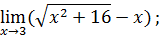




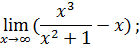


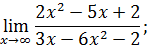
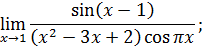
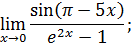
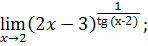



 .
.









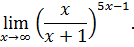
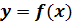 . Определить вид разрывов и изобразить график функции в окрестности этих точек.
. Определить вид разрывов и изобразить график функции в окрестности этих точек.
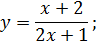




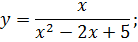




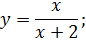




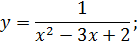








 следующих функций:
следующих функций: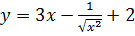 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
 , если
, если 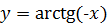 .
. , если
, если 
 , если
, если 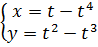
 ;
;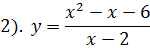
 на отрезке
на отрезке 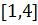 .
. в точках её пересечения с осью абсцисс.
в точках её пересечения с осью абсцисс.

 .
.









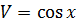

 .
. – производная сложной функции
– производная сложной функции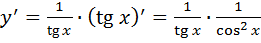
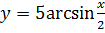

 (обратить внимание
(обратить внимание  это показательная функция)
это показательная функция)


 , если
, если 

 , если
, если 

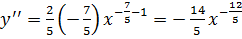
 , если
, если  ;
; 

 . Т.к. функция представляет собой многочлен, то ни наклонных, ни горизонтальных асимптот нет
. Т.к. функция представляет собой многочлен, то ни наклонных, ни горизонтальных асимптот нет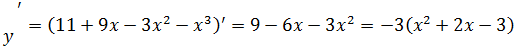
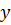
 ;
;
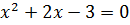 ;
;
 ;
;
 ;
;
 .
.
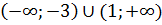 ;
; .
. максимум;
максимум;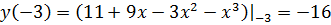 мининум.
мининум.

 ;
;
 .
.

 ;
;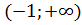 .
.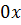 найти не можем (сложно)
найти не можем (сложно) .
. :
:

 .
.
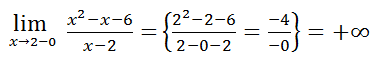

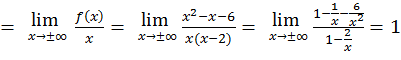
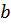
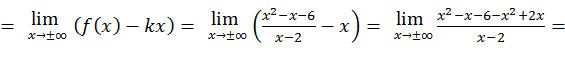
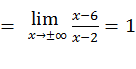
 .
.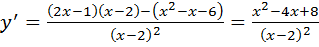
 .
.
 выполнено неравенство
выполнено неравенство  , поэтому на интервале
, поэтому на интервале  график функции является вогнутым. При
график функции является вогнутым. При 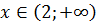 выполняется неравенство
выполняется неравенство  , поэтому на интервале
, поэтому на интервале  график функции является выпуклым.
график функции является выпуклым. , поэтому с осью
, поэтому с осью  . Далее,
. Далее, 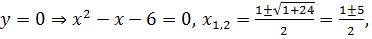
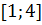 .
.

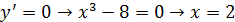
 не существует
не существует  , но в этой точке не существует сама
, но в этой точке не существует сама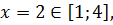 значит, она нам нужна.
значит, она нам нужна.



 – наибольшее значение
– наибольшее значение 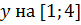 ;
; – наименьшее значение
– наименьшее значение 

 имеет вид:
имеет вид: ,
, ;
; ;
; .
.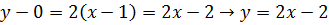 ;
; .
.