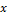|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ОБРАЗЕЦ ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ №2Стр 1 из 2Следующая ⇒
ОБРАЗЕЦ ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ №1 «Аналитическая геометрия» Вариант 0 1. Разложить вектор 2. Найти длину вектора
3. Найти вектор 4. Вычислить угол между диагоналями параллелограмма, построенного на векторах 5. Найти направляющие косинусы вектора силы 6. Найти вектор 7. Определить, лежат ли точки А(1, 2, 3); В(0, 5, 5); С(3, -1, -1); D(-2, 14, 9) в одной плоскости. 8. В треугольнике АВС известны координаты вершины А(4, 0) и уравнения высоты 9. Найти длину высоты пирамиды ABCD, опущенную из вершины D, если D(1, 6, 3), А(4, 5, 2), В(-1, 11, 6) и С(2, -1, 3). 10. Найти радиус и координаты центра окружности, заданной уравнением.
I. Решение
 по векторам по векторам 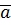 и и  – это значит представить – это значит представить  в виде в виде 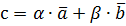 , где α и β пока неизвестные числа. Переходя к координатам, получим: , где α и β пока неизвестные числа. Переходя к координатам, получим: 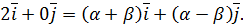
В результате приходим к системе уравнений:
решением которой являются α = 1 и β = 1. Отсюда Ответ: 2. Решение Как известно, модуль вектора равен корню квадратному из скалярного квадрата этого вектора
Ответ: 3. Решение В силу коллинеарности вектор Ответ: 4. Решение Известно, что диагонали параллелограмма можно найти
т.к. векторы
Ответ: 5. Решение Находим направляющие косинусы вектора силы
момент силы как векторное произведение вектора
Ответ:
6. Решение Найдем вектор Поскольку вектор Так как Ответ: 7. Решение Рассмотрим три вектора
следовательно, векторы компланарны и точки лежат в одной плоскости. 8. Решение
Составим уравнение АС, для чего определим её угловой коэффициент из условия перпендикулярности АС и ВЕ:
Зная угловой коэффициент и одну точку, находим уравнение АС:
Находим координаты D как точки пересечения медианы BD и стороны AC:
Находим координаты вершины С, используя то, что D делит отрезок АС пополам, С(8, -6). Зная координаты всех вершин треугольника, составляем уравнения сторон АВ и ВС как прямых, проходящих через заданные точки.
BC:
9. Решение Длина высоты равна расстоянию от вершины D до плоскости АВС. Составим уравнение этой плоскости, воспользовавшись уравнением плоскости, проходящей через три точки:
Находим теперь расстояние от D до плоскости АВС:
Ответ: h = 3 10. Решение Приводим уравнение к каноническому виду, выделяя полные квадраты
Полученное уравнение определяет окружность радиуса 2 с центром в точке (5, -4).
Ответ: Окружность R = 2, центр (5, -4)
ОБРАЗЕЦ ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ №2 «Предел и непрерывность функции» Вариант 0 I. Найти пределы функций:
и изобразить график функции в окрестности этих точек.
I. Решение Нам потребуются следующие сведения из теории пределов:
Эквивалентности:
Разложим числитель на множители:
Имеем
Домножим числитель и знаменатель на
Разложим квадратный трехчлен в знаменателе и воспользуемся тем, что
Получаем
Функция непрерывна всюду, кроме точки в которой знаменатель обращается в нуль, т.е.
Характер точки разрыва зависит от того, какое из этих трех условий нарушается В нашем примере функция не существует в точке Для существования предела функции в точке должны существовать и быть равны односторонние пределы в этой точке:
Это также поможет нам построить правильно график
Поиск по сайту: |
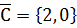 по векторам
по векторам 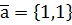 и
и 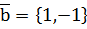
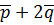 , если
, если 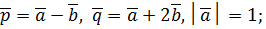
 .
. , коллинеарный вектору
, коллинеарный вектору 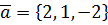 и удовлетворяю-щий условию
и удовлетворяю-щий условию  .
.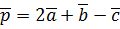 и
и  , где
, где 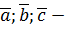 единичные взаимноперпендикулярные векторы (косинус угла).
единичные взаимноперпендикулярные векторы (косинус угла).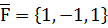 , приложен-ной в точке В(5, 1, 0), и момент этой силы относительно точки А(3, 2, -1).
, приложен-ной в точке В(5, 1, 0), и момент этой силы относительно точки А(3, 2, -1).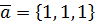 и
и  и образующий с осью OX тупой угол, если
и образующий с осью OX тупой угол, если 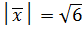 .
. и медианы
и медианы 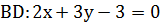 . Составить уравнения сторон треугольника.
. Составить уравнения сторон треугольника.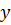 2
2 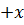 2
2 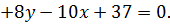
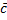
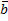

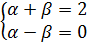 ,
,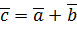 .
.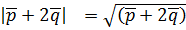 2. Находим скалярный квадрат
2. Находим скалярный квадрат 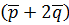 2
2 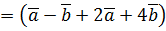 2
2  2
2  2
2  2
2 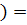
 Отсюда
Отсюда 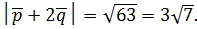
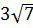
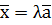 , где λ – пока неизвестный множитель. Для его определения используем второй пункт условия (
, где λ – пока неизвестный множитель. Для его определения используем второй пункт условия (  Отсюда
Отсюда  и
и 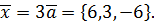
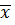 =
= 
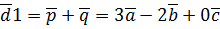
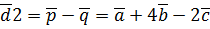
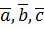 представляют собой единичные взаимно перпендику-лярные вектора, то
представляют собой единичные взаимно перпендику-лярные вектора, то 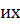 можно считать координатным базисом, тогда для нахождения требуемого угла воспользуемся формулой
можно считать координатным базисом, тогда для нахождения требуемого угла воспользуемся формулой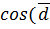 1
1 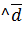 2)
2) 
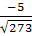
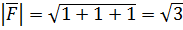
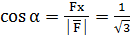
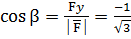
 ,
,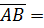
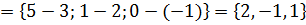 на вектор
на вектор 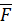 :
: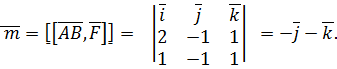 Следовательно,
Следовательно, 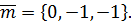
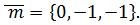
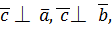 следовательно,
следовательно,
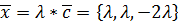 .
.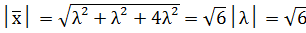 , то λ
, то λ 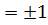 . Вектор
. Вектор 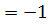 и
и  .
.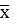 =
= 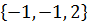 .
.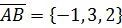 ,
, 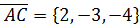 и
и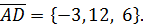 если точки А, В, С, D лежат в одной плоскости, то векторы
если точки А, В, С, D лежат в одной плоскости, то векторы  компланарны. Для проверки составляем смешанное произведение этих векторов:
компланарны. Для проверки составляем смешанное произведение этих векторов:
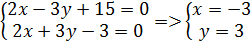

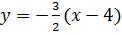 или
или 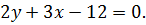

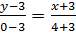
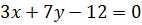
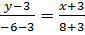
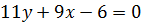 .
.
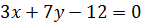
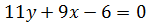
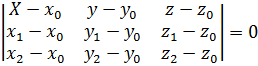
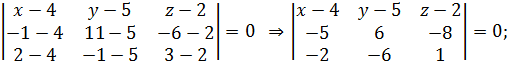
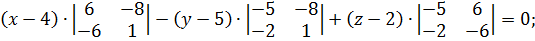
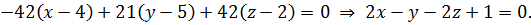
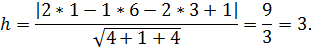
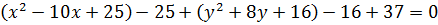 или
или
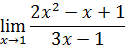

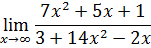

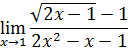



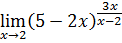
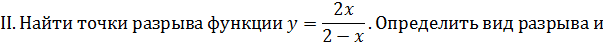

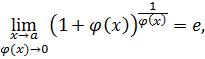
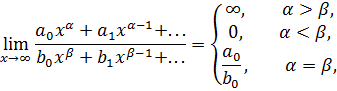
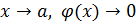 .
. ,
,
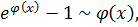
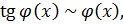
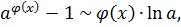

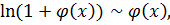
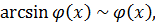


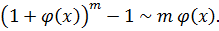
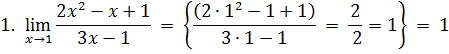
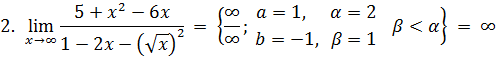
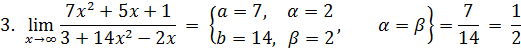
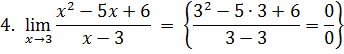
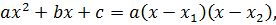 где
где 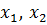 – корни уравнения
– корни уравнения 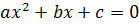 .
.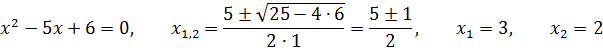
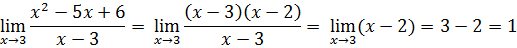

 , тогда согласно формуле
, тогда согласно формуле 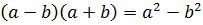 получаем
получаем

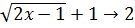 при
при 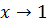 :
: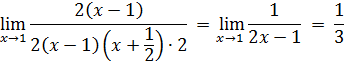

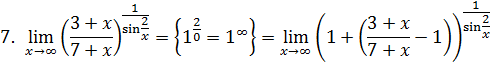
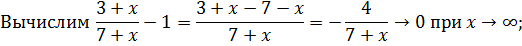

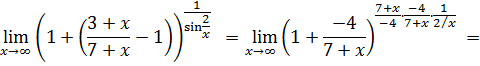


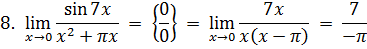
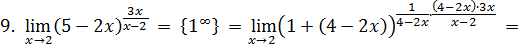
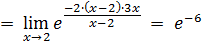
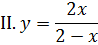
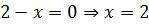 . Это и есть возможная точка разрыва. По определению функция
. Это и есть возможная точка разрыва. По определению функция 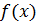 называется непрерывной в точке
называется непрерывной в точке 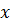 , если
, если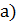 Она определена в этой точке.
Она определена в этой точке.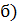 Существует предел функции в
Существует предел функции в 
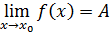
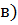 И этот предел равен значению функции в точке
И этот предел равен значению функции в точке 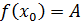
 .
.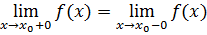
 в окрестности точки разрыва
в окрестности точки разрыва