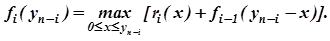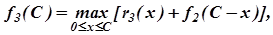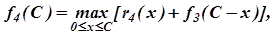РЕШЕНИЕ ЗАДАЧ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Оптимизация решения о капиталовложениях в

несколько объектов единовременно

Допустим, имеется возможность вложения средств С в группу из n предприятий на реконструкцию и модернизацию оборудования. Известен возможный прирост продукции на каждом предприятии в зависимости от выделенных ему средств r_i(x); .

Необходимо таким образом распределить инвестиции С между предприятиями, чтобы общий прирост выпуска продукции на всех n предприятиях в сумме был максимальным.

Составим основное функциональное уравнение. Обозначим через f₁ – максимально возможный прирост выпуска продукции на одном предприятии при различных значениях вкладываемых средств х. Каждому значению х отвечает определённый результат r₁(x):

где y_n-1 – допустимая сумма средств, которая может быть вложена в одно предприятие – это допустимое состояние процесса на начало первого шага вычислений.

На следующем шаге - оптимальный эффект от вложения средств в два предприятия получаем максимизируя объём прироста продукции на втором предприятии r₂(x) плюс оптимальный результат, полученный на предыдущем шаге:

где y_n-2 – средства, вкладываемые в два предприятия;

х – средства, выделяемые второму предприятию;

(y_n-2 – x) – средства, вкладываемые в первое предприятие.

В общем случае функциональное уравнение задачи, позволяющее максимизировать эффект, получаемый на i-м шаге, плюс оптимальное решение, полученное на предыдущем шаге, имеет вид:

Задача. Составить оптимальный план распределения капиталовложений между четырьмя предприятиями (проектами) в размере С = 100 млн. ден. ед.

Таблица 1

На первом этапе решения задачи динамического программирования, рассмотрим программу вложения средств в предприятие по шагам. На первом шаге максимизируем отдачу f₁(C) от вложения средств x₁ в одно (первое) предприятие:

Таблица 2

Отдача от средств, вкладываемых в 1-ое предприятие

На втором шаге максимизируем отдачу f₂(C) от вложения средств в два предприятия, из которых x₂ вкладывается во второе предприятие, с учётом результата, полученного на предыдущем шаге, при этом вложения в первое предприятие составят (С – х₁):

Таблица 3

Отдача от средств, вкладываемых во 2-ое предприятие и их остатков, вкладываемых в 1-ое предприятие

На третьем шаге максимизируем отдачу f₃(C) от вложения средств в три предприятия, из которых x₃ вкладывается в третье предприятие, с учётом результата, полученного на предыдущем шаге:

Таблица 4

Отдача от средств, вкладываемых в 3-е предприятие и их остатков (С – х₂), вкладываемых в 1-ое и 2-ое предприятия

На четвёртом шаге максимизируем отдачу f₄(C) от вложения средств в четыре предприятия, из которых x₄ вкладывается в четвёртое предприятие, с учётом результата, полученного на предыдущем шаге:

Таблица 5

Отдача от средств, вкладываемых в 4-ое предприятие и их остатков (С – х₃), вкладываемых в 1-ое, 2-ое и 3-е предприятия

На втором этапе решения задачи динамического программирования, проанализируем таблицы в обратном порядке. Максимальный прирост отдачи от вложения средств в размере 100 млн. ден. ед. на четырёх предприятиях составит 91 млн. ден. ед. (табл. 5). При этом в 4-ое предприятие следует вложить х₄ = 40 млн. ден. ед. Остаток средств 100 – 40 = 60 млн. ден. ед. вкладывают в развитие 1-го, 2-го и 3-го предприятий. Из табл. 4 видно, что из этой суммы в 3-е предприятие следует вложить х₃ = 40 млн. ден. ед. Остаток средств - 60 – 40 = 20 млн. ден. ед. вкладывают в развитие 1-го и 2-го предприятий. Из табл. 3 видно, что из этой суммы во 2-е предприятие следует вложить всю оставшуюся сумму х₂ = 20 млн. ден. ед. Вложение средств в 1-ое предприятие нерентабельно.

f = 91, x₁ = 0, x₂ = 20, x₃ = 40, x₄ = 40.

В А Р И А Н Т Ы К З А Д А Н И Ю № 2

ГЛОССАРИЙ

ИССЛЕДОВАНИЕ ОПЕРАЦИЙ - прикладное направление математики и экономической кибернетики, непосредственно используемое для решения практических организационных (в том числе экономических) задач. Это - комплексная научная дисциплина. Круг проблем, изучаемых ею, пока недостаточно определен. Иногда исследование операций понимают очень широко, включая в это понятие ряд чисто математических методов, иногда, наоборот, очень узко, как практическую методику решения строго определенного перечня задач с помощью экономико-математических моделей.

Сущность задач исследования операций - поиск путей рационального использования имеющихся (весьма разнообразных) ресурсов для достижения поставленных целей. Соответственно, операцией называют сложный процесс с ярко выраженной целью или, шире, совокупность действий, направленных на достижение некоторой цели. Поскольку обычно возможностей для этого много, выбираются те или иные стратегии («альтернативы») - это позволяет оценивать влияние отдельных факторов на результат, выявлять «узкие места» и т.д.

Исследование операций дает эффект в наиболее сложных случаях. Например, расширение выпуска продукции на заводе требует одновременного взаимосвязанного решения множества частных проблем: реконструкции предприятия, заказа оборудования, сырья и материалов, подготовки кадров, подготовки рынка сбыта, совершенствования технологии, изменения системы оперативно-производственного планирования и диспетчирования, организационной перестройки, перемещения руководящих работников и т. д. При анализе возможных последствий принимаемых решений приходится учитывать такие факторы, как случайность и риск. К решению столь сложных задач привлекают экономистов, математиков, статистиков, инженеров, социологов и психологов.

Основные этапы операционного исследования следующие:

- постановка задачи и выделение критерия эффективности (например, им может быть рост прибыли предприятия в результате расширения выпуска продукции):

- построение математической модели изучаемой системы;

- нахождение решения с помощью модели;

- проверка модели и полученного с ее помощью решения;

- построение процедуры подстройки (т. е. исправления) решения на случай, если изменятся условия;

- осуществление решения.

Таким способом решаются задачи, связанные с процессом создания и хранения запасов, распределением ресурсов, обслуживанием, заменой оборудования и др. Количественные методы исследования операций строятся на основе достижений экономико-математических и статистических дисциплин (теории массового обслуживания, оптимального программирования и т. д.). Эти методы зародились накануне второй мировой войны, когда в Англии на одной радиолокационной станции была создана группа специалистов для решения технических задач при помощи математики. Они сосредоточили внимание на сравнении эффективности путей решения задач, поиске оптимального решения. Участие в этой группе представителей разных специальностей предопределило комплексный, или, как теперь принято говорить, системный подход. В дальнейшем выяснилось, что такой подход особенно плодотворен при решении производственных задач. В настоящее время в этом направлении работают сотни исследовательских учреждений и групп в десятках стран.

В нашей стране особенно широко используются такие ветви исследования операций, как сетевое планирование и управление, теория массового обслуживания. Это повышает обоснованность и эффективность хозяйственных решений.

ЗАДАЧИ МАССОВОГО ОБСЛУЖИВАНИЯ класс задач исследования операций, заключающихся в нахождения оптимальных параметров систем массового обслуживания (см. в первом разделе статью «Теория массового обслуживания»). Такие задачи успешнее всего решаются методами машинной имитации: ЭВМ воссоздает искусственно картину того, что может произойти в исследуемой системе обслуживания при различных условиях, и выдает статистические данные, как если бы они были получены при наблюдении за реальным действием системы (например, магазина, склада, порта и т.д.). Анализ таких данных позволяет выявлять «узкие» места в системе и рационализировать ее.

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ - первая по времени возникновения и на сегодняшний день самая распространенная область оптимального программирования. Она посвящена теории и методам решения экономико-математических экстремальных задач, характеризующихся линейной зависимостью между переменными.

Первооткрыватель линейного программирования - советский ученый, академик, лауреат Ленинской, государственных и Нобелевской премий Л.В. Канторович. Он в 1939 г., занявшись вопросами планирования работы агрегатов фанерной фабрики, решил математически несколько задач: о наилучшей загрузке машин, о раскрое материалов с наименьшими расходами, о распределении грузов по нескольким видам транспорта и др. При этом он разработал универсальный метод решения таких задач, а также различные алгоритмы реализующие его.

В 40-50-х годах, многое сделали в этой области американский экономист Т. Купманс и математик Дж. Данциг. Последнему принадлежит и сам термин «линейное программирование». Слово «программирование», объясняется здесь тем, что неизвестные переменные, которые отыскиваются в процессе решения задачи, обычно в совокупности определяют программу (план) работы некоторого Экономического объекта. При этом задача обязательно носит экстремальный характер, т.е. состоит в отыскании экстремума (максимума или минимума) целевой функции. Им могут быть, например, максимум продукции, или максимум прибыли, или минимум затрат и т.д. Прилагательное «линейное» означает прямую пропорциональную зависимость между переменными. Например, увеличение на 5% количества рабочих часов и заготовок повышает выработку на те же 5%. Поскольку здесь рассматриваются именно такие взаимосвязи, метод назван «линейным программированием».

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА - раздел прикладной математики, который занимается методами и правилами обработки, анализа и использования статистических данных для научных и практических выводов. Сами правила строятся безотносительно к тому, какие статистические данные обрабатываются (физические, экономические, биологические и т.д.). Однако обращение с ними обязательно требует понимания сущности явления, изучаемого с помощью этих правил. К экономике математическая статистика применима по той причине, что экономические данные всегда представляют собой статистические сведения, т. е. сведения об однородных совокупностях объектов и явлений. Такими однородными совокупностями могут быть выпускаемые промышленностью изделия, персонал промышленности, данные о прибылях предприятий и т.д. В настоящее время существуют разные определения сущности математической статистики, и не следует удивляться, если вы увидите в одной книге утверждение, что математическая статистика - это наука о принятии решений в условиях неопределенности, а в другой, что это наука, объясняющая данные статистических наблюдений при помощи моделей. Математическая статистика помогает делать выводы не из сплошного рассмотрения всей совокупности изучаемых явлений, а из ее выборки, причем выборки случайной. Последнее означает, что каждая единица, включенная в выборку, могла быть с равными шансами заменена любой другой. Математическая статистика позволяет на основании анализа течения событий в прошлом предсказывать вероятное развитие изучаемого явления в будущем (если не изменятся существенно внешние или внутренние условия).

Задачи математической статистики можно разделить на пять основных типов: а) оценка статистических данных; б) сравнение этих данных с каким-то стандартом и между собой (это имеет особое значение при эксперименте); в) исследование связей между статистическими данными и их группами. Эти три первых типа позволяют вынести суждение описательного характера об изучаемых явлениях, подверженных по каким-то причинам искажающим случайным воздействиям. Следующий, четвертый тип задач связан с нахождением наилучшего варианта изменения изучаемых данных. И наконец, пятый тип задач связан с проблемами предвидения и развития - здесь важное место занимают задачи анализа временных рядов.

Методы математической статистики применяются в ряде направлений исследования операций, например, в теории массового обслуживания, а также в эконометрических исследованиях, где на основе обработки статистических данных строятся математические модели экономических процессов и проверяется их соответствие действительности.

МАТРИЧНАЯ МОДЕЛЬ - модель, выраженная в виде таблицы (матрицы). Она применяется в межотраслевом балансе (МОБ), при составлении планов предприятий и в других случаях. Широкое распространение матричных моделей связано с тем, что запись данных в табличной форме облегчает их введение в ЭВМ и дает наглядное представление результатов расчета.

МАШИННАЯ ИМИТАЦИЯ - экспериментальный метод изучения экономики с помощью электронных вычислительных машин. Процесс имитации заключается в следующем: сначала строится математическая модель изучаемого объекта, затем эта модель преобразуется в программу работы ЭВМ. В машину вводятся необходимые данные и ведется наблюдение над тем, как изменяются интересующие исследователя показатели.

Предположим, мы хотим изучить, как будет расти производство на заводе при нескольких вариантах его развития: если мы построим дополнительный цех, если заменим оборудование в существующих цехах, если применим новую систему экономического стимулирования и т. д. Математическая модель завода, которую мы для этого разработаем, должна будет содержать необходимые для последующих расчетов сведения: данные о том, какое оборудование имеется сейчас, какое изменение в производительности каждого вида оборудования возможно при его замене; данные о затратах, квалификации и заработной плате различных групп работающих (на них по-разному будет воздействовать тот или иной способ стимулирования) и т. д. Все эти сведения вводятся в машину, и на ней имитируется, или, как еще говорят, проигрывается, будущий процесс развития завода. Обычно мысленно так мы и делаем, когда пытаемся представить себе, что будет, если мы примем такое-то решение. Нетрудно ответить, когда вариантов немного и условия задачи просты. А когда условия задачи, как это всегда бывает в экономике, сложны и трудно представить себе будущий ход событий, то без машинной имитации не обойтись. Машина сократит время, за какие-нибудь минуты «проиграет» развитие завода при всех интересующих вас вариантах, да еще покажет, какой из них лучший.

ОПТИМАЛЬНОЕ ПРОГРАММИРОВАНИЕ - общий термин, которым обозначаются два взаимосвязанных комплекса научных дисциплин. С одной стороны - такие экономические дисциплины, как методы разработки планов, регулирования деятельности хозяйственных звеньев, и с другой - математические методы и дисциплины, объединенные общим термином «математическое программирование»: линейное программирование, нелинейное программирование, дискретное программирование, целочисленное программирование, динамическое программирование, выпуклое программирование и др. Оптимальное программирование (планирование) означает распределение ограниченных ресурсов наилучшим образом для достижения поставленных целей.

СЕТЕВОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ (СПУ) метод планирования и управления, основанный на использовании ЭВМ и сетевых графиков. Такой график представляет цепи работ и событий, отражая их технологическую последовательность и связь.

На его основе ЭВМ может произвести анализ состояния процесса в каждый заданный момент времени, определить последовательности работ, которые могут задержать выполнение плана к намеченному сроку (критический путь) и, таким образом, «посоветовать» руководству оперативно принять необходимые меры.

Впрочем, существуют и такие системы СПУ, которые ориентированы не на критерий времени, а, например, на сокращение стоимости работ.

СИСТЕМНЫЙ АНАЛИЗ можно рассматривать как дальнейшее развитие идей кибернетики. Он позволяет исследовать категории, общие для многих дисциплин и относящиеся к так называемым системам, которые изучаются любой наукой.

Эта дисциплина непосредственно связана с математической логикой и изучает, например, такие общие для любых систем объекты, как «вход», «выход», «цель», «обратная связь», а также «рост», «взаимодействие» и др. Она вооружает различные науки, в том числе экономику, системным подходом.

Когда речь идет об изучении действующих, развивающихся систем, какими являются и любой экономический объект, и экономика в целом, то системное исследование может иметь два аспекта: генетический и функциональный, т.е. изучение системы в развитии и изучение ее реального действия, функционирования.

Главный инструмент системного анализа - модель изучаемой системы. Анализ включает:

- анализ и описание принципов по- строения и работы системы в целом;

- анализ особенностей всех компонентов системы, их взаимозависимостей и внутреннего строения;

- установление сходства и различия изучаемой системы и других систем;

- перенос по определенным правилам свойств модели на свойства изучаемой системы.

СИСТЕМНЫЙ ПОДХОД К ИЗУЧЕНИЮ ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ - комплексное изучение экономики как единого целого с позиций системного анализа.

Поскольку главная отличительная особенность большой или сложной системы - тесная взаимосвязь всех ее элементов и частей, то системный подход к анализу экономических явлений означает учет этих взаимосвязей, изучение отдельных хозяйственных объектов как структурных частей более сложных систем, выявление роли каждой из них в общем процессе функционирования экономики. Математический анализ экономических процессов показал возможности и условия совместной оптимизации как структурных частей системы, так и системы в целом. Принимая частное решение по отдельному хозяйственному вопросу, мы должны знать все прямые и косвенные, близкие по времени и отдаленные последствия этого решения.

ТЕОРИЯ ИГР - раздел современной математики, изучающий так называемые «конфликтные ситуации» (т.е. ситуации, при которых интересы участников противоположны или, во всяком случае, не совпадают). Выдающийся математик ХХ в. Джон Нейман пришел к идеям теории игр, пытаясь математически описать характерные для рыночной экономики явления конкуренции. В наиболее простом случае речь идет о противоборстве только двух противников, например двух конкурентов, борющихся за рынок сбыта. В более сложных случаях в «игре» участвуют многие, причем они могут вступать между собой в постоянные или временные коалиции, союзы. Суть «игры» в том, что каждый из участников принимает такие решения (т.е. выбирает стратегию действий), которые, как он полагает, обеспечивают ему наибольший выигрыш или наименьший проигрыш. Эти решения отражаются в таблице, которая называется платежной матрицей. Существует такая точка («седловая»), в которой достигается равновесие, приемлемое для партнеров.

Чисто математическая и потому весьма абстрактная теория игр, разумеется, далеко не полно отражает сложные процессы, происходящие в реальной экономике.

Математические приемы теории игр могут применяться для решения многочисленных практических экономических задач: например, на промышленных предприятиях для выбора оптимальных решений в области повышения качества продукции, определения запасов и т. д. «Противоборство» здесь происходит в первом случае между стремлением выпустить больше продукции (затратить на нее меньше труда) и сделать ее лучше, т.е. затратить больше труда; во втором случае - между желанием запасти побольше, чтобы быть застрахованным от случайностей и запасти поменьше, чтобы не омертвлять средства. Многие задачи теории игр могут быть сведены к задаче линейного программирования, и наоборот.

ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ - дисциплина, раздел исследования операций, которая рассматривает разнообразные процессы в экономике как процессы обслуживания, т.е. удовлетворения каких-то запросов, заказов. Например, обслуживание кораблей в порту (их разгрузка и погрузка), обслуживание токарей в инструментальной кладовой цеха (выдача им резцов), обслуживание клиентов в банке и т.д. При всем разнообразии эти процессы имеют общие черты: «требование на обслуживание», «очередь требований», «канал обслуживания» (место у причала, окно в банке). Теория массового обслуживания изучает статистические закономерности поступления «требований» и на этой основе вырабатывает решения, т.е. порядок обслуживания, при котором затраты времени на ожидание «в очереди», с одной стороны, и на простой «каналов обслуживания» - с другой, были бы наименьшими., Всю систему производства и потребления товаров можно трактовать как систему массового обслуживания, где встречаются люди (клиенты) и товары. Некоторые ученые делают из этого весьма широкие выводы. Они склонны считать сумму потерь времени на ожидание в очередях и на простой каналов обслуживания (хранение товаров на складах) за меру эффективности изучаемой экономической системы: чем меньше потери, тем выше эффективность.

ТЕОРИЯ РЕШЕНИЙ, или теория принятия решений - дисциплина (область исследования операций), которая изучает математические и математико-статистические правила принятия решений, в первую очередь - экономических. Иногда это название применяют к более общей теории, которая изучает вообще правила принятия решений (не только основанные на математике), т.е. проблемы психологические, этические и т.д.

Одним из примеров применения методов математико-статистической теории принятия решений является организация статистического контроля качества на предприятии.

ЭВРИСТИЧЕСКИЕ МЕТОДЫ решения экономико-математических задач - методы, в которых используются индивидуальные особенности каждой решаемой задачи, ранее приобретенный опыт и т. д. Это новое, еще слабо разработанное направление, однако некоторые экономисты-математики возлагают на него большие надежды. Эвристические методы (или коротко - эвристика) позволяют решать задачи с меньшими затратами машинного времени, ибо при обычных, полностью алгоритмированных методах машина решает задачу от начала до конца. При этом, как бы хорошо ни была составлена программа, она делает массу ненужных вычислений, перебирая вариант за вариантом возможного решения. Эвристические методы позволят, видимо, отказаться от части ненужных расчетов - как это делает человек, например, при решении математических задач или при игре в шахматы.

Кроме того, перспективно соединение точных алгоритмических методов с эвристическими.

ЭКОНОМИКО-МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ - описание экономических процессов в виде математических моделей.

Многие модели пригодны для решения разных экономических задач. Например, с помощью одной и той же модели линейного программирования можно решать задачи о наилучшем размещении посевов сельскохозяйственных культур, о наиболее полной загрузке оборудования на заводе, о наивыгоднейшем варианте перевозок различных продуктов из пунктов производства в пункты потребления. С другой стороны, существуют такие задачи, которые могут решаться с помощью разных моделей, и тогда перед экономистами возникает проблема, какая из моделей точнее или удобнее, требует меньшего количества вычислений. Усложняя модель, чтобы сделать ее более точной и подробной, мы должны знать: компенсирует ли полученная точность, результатов возросшие вычислительные трудности и материальные затраты? И наоборот, решая исключить какой-то элемент из модели, чтобы сделать ее проще, должны оценить потери в ее достоверности, т.е. не обойдутся ли они дороже, чем выигрыш от упрощения расчетов?

ЭКСПЕРТНЫЕ ОЦЕНКИ - заключения специалистов по какому-либо вопросу. В принципе их нельзя считать вполне объективными, поскольку на специалиста-эксперта могут воздействовать различные побочные факторы. Разрабатываются научные методы такой обработки индивидуальных экспертных оценок, чтобы они давали в совокупности более или менее объективные ответы. Это достигается путем специально подготовленных методов формирования групп экспертов, продуманных форм вопросов и ответов, приспособленных к обобщению с помощью электронно-вычислительной машины. Разработка таких методов в настоящее время развилась в самостоятельную область науки об управлении.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

а) Основная литература

1. Исследование операций в экономике / под ред. Н.Ш. Кремера. - М.: 1997.

2. Зайченко Ю.П. Исследование операций / Ю.П. Зайченко. – Киев: Вища школа, 1979

3. Вентцель Е.С. Исследование операций / Е.С. Вентцель. - М.: Наука, 1972.

4. Вентцель Е.С. Исследование операций. Задачи, принципы, методология / Е.С. Вентцель. - М.: Наука, 2005.

5. Гермейер Ю.Б. Введение в теорию исследования операций / Ю.Б. Гермейер. - М.: Наука, 1971.

6. Афанасьев М.Ю. Исследование операций в экономике: модели, задачи, решения: учеб. пособие / М.Ю. Афанасьев, Б.П. Суворов. - М.: ИНФРА-М, 2003. 444 с.

7. Косоруков О.А. Исследование операций / под общ. ред. д.э.н., проф. Н.П.Тихомирова / О.А. Косоруков, А.В. Мищенко. - М.: Экзамен, 2003. 448 с.

8. Эддоус М. Методы принятия решений / М. Эддоус, Р. Стэнсфилд. - М.: ЮНИТИ, 1997.

9. Морз Ф.М. Методы исследования операций / Ф.М. Морз, Д.Е. Кимбел. – М.: "Сов. радио", 1956.

10. Саати Т.Л. Математические методы исследования операций / Т.Л. Саати. – М.: Воениздат 1963.

11. Баумоль У. Экономическая теория и исследование операций. / У. Баумоль. – М.: Прогресс, 1965.

12. Исследование операций / под ред. Дж. Моудера, С. Элмаграби. – М.: Мир, 1981. Т.1. – 712 с., Т.2. – 677 с.

13. Кофман А. Методы и модели исследования операций / А. Кофман, А. Анри-Лабордер. – М.: Мир, 1977.

14. Костевич Л.С. Теория игр. Исследование операций / Л.С. Костевич. - Минск., 1982

15. Романовский И.В. Исследование операций и статистическое моделирование / И.В. Романовский. – СПб.: Санкт-Петербургский гос. ун-т, 1994.

16. Таха Х. Введение в исследование операций / Х. Таха. – М.: Мир, 1985.

17. Таха Х.А. Введение в исследование операций / Х.А. Таха. - М.: Издательский дом "Вильямс", 2001.

18. Черчмен У. Ввелдение в иссдедование операций: пер с англ. / У. Черчмен, Р. Акоф, Л. Арноф. – М.: Наука, 1968.

19. Шапкин А.С. Математические методы и модели исследования операций / А.С. Шапкин, Н.П. Мазаева. – М.: «Дашков и К^о», 2004. 400 с.

20. Вагнер Г. Основы исследования операций / Г. Вагнер. - М.: Мир, 1972.

б) Дополнительная литература

1. Акулич И.Л. Математическое программирование в примерах и задачах / И.Л. Акулич. - М.: Высш. шк., 1996.

2. Математическое программирование / Кузнецов Ю.Н. и др. -М.: Высш. шк., 1976.

3. Калихман И.Л. Сборник задач по математическому программированию / И.Л. Калихман. - М.: Высш. шк., 1975.

4.Карасев А.И. Математические методы и модели в планировании / А.И. Карасев, Н.Ш. Кремер, Т.И. Савельев. - М.: Экономика, 1987.

5. Курицкий Б.Я. Поиск оптимальных решений средствами EXCEL 7.0 / Б.Я. Курицкий. - СПб.: 1997.

6. Лопатников Л.И. Экономико-математический словарь. Словарь современной экономической науки / Л.И. Лопатников. - М.: Издательство "АВF", 1996. 704 с.

7. Колесников А.Н. Краткий курс математики для экономистов: учеб. пособие / А.Н. Колесников. - М.: ИНФРА-М, 1997.- 208 с.

8. Красс М.С. Математика для экономических специальностей: учебник / М.С. Красс. - М.: ИНФРА-М, 1998.- 464 с.

9. Высшая математика для экономистов: учеб. пособие для вузов / под ред. Н.Ш.Кремера. - М.: Банки и биржи, ЮНИТИ, 1997.- 439 с.

10. Харин Ю.П. Основы имитационного и статистического моделирования: учеб. пособие для вузов. Ю.П. Харин, В.И. Малюгин, В.П. Кирлица. – Минск: Дизайн ПРО, 1997.

11. Шебеко Ю. Имитационное моделирование и ситуационный анализ бизнес-процессов принятия управленческих решений / Ю. Шебеко. – М.: ТОРА – ИнфоЦентр, 2000.

12. Банди Б. Основы линейного программирования: пер. с англ. / Б. Банди. - М.: Радио и связь, 1989. -176 с

в) Методическая литература

1. Амелин С.В. Методические указания по выполнению лабораторных работ по курсу "Исследование операций в экономике " для студ. спец. 060800 дневной формы обучения / С.В. Амелин. - Воронеж: ВГТУ 2000 г. 27 с

2. Аронович А.Б. Сборник задач по исследованию операций: учеб. пособие для студ. экономич. специальностей вузов / А.Б. Аронович, М.Ю. Афанасьев, Б.П. Суворов. - М.: Изд-во МГУ, 1997.

3. Цисарь И.Ф. Компьютерное моделирование экономики / И.Ф. Цисарь, В.Г. Нейман. - М.: Диалог-МИФИ, 2002. 304 с.

4. Цисарь И.Ф. Лабораторные работы на персональном компьютере / И.Ф. Цисарь. - М.: Экзамен, 2002. 224 с.

5. Гельман В.Я. Решение математических задач средствами Excel: Практикум /. В.Я. Гельман. - СПб.: Питер, 2003. 240 с.

6. Таганов Д.Н. SPSS: Статистический анализ в маркетинговых исследованиях / Д.Н. Таганов. - СПб.: Питер, 2005. 192 с.

7. Дубнов П.Ю. Обработка статистической информации с помощью SPSS. П.Ю. Дубнов. - М.: АСТ: НТ Пресс, 2004. 221 с.

8. Плис А.И. Практикум по прикладной статистике в среде SPSS. А.И. Плис. - Учеб. пособие. М.: Финансы и статистика, 2004. 288 с.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по выполнению самостоятельной работы и

индивидуальных заданий по дисциплине

"Исследование операций"

Составитель

Амелин Станислав Витальевич

В авторской редакции

Подписано в печать 05.06.2012.

Формат 60 х 84 / 16. Бумага для множительных аппаратов.

Усл. печ. л. 3,4. Уч.-изд. л. 3,2. Тираж 200 экз. «С» 239.

Зак. № 339.

ФГБОУ ВПО "Воронежский государственный технический

университет"

394026 Воронеж, Московский просп., 14

Поиск по сайту: