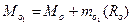|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Напишите и сформулируйте необходимые и достаточные условия равновесия произвольной плоской системы сил? ⇐ ПредыдущаяСтр 2 из 2
- для равновесия плоской системы сил, необходимо и достаточно, чтобы суммы проекций этих сил на каждую их двух прямоугольных осей координат, расположенных в плоскости действия сил, были равны нулю и сумма алгебраических моментов сил относительно любой точки, находящейся в плоскости действия сил, также была равная нулю.
- для равновесия плоской системы сил, необходимо и достаточно, чтобы суммы моментов всех сил относительно любых трёх точек, не лежащих на одной прямой, были равны нулю.
- для равновесия плоской системы сил, необходимо и достаточно, чтобы суммы моментов всех сил относительно двух любых точек А и В и сумма проекция на ось Ох, не перпендикулярную прямой, проходящей через точки А и В/, были ранвы нулю.
19. Напишите и сформулируйте три формы уравнений равновесия произвольной плоской системы сил смотри.24 20. Какие статические инварианты Вам известны? Запишите соответствующие формулы. - Величины, которые не изменяются при каком-либо преобразовании, называются инвариантами по отношению к этим преобразованиям. - Величина и направление главного вектора не зависит от выбора центра приведения.
- Скалярное произведение главного момента произвольной пространственной системы сил на главный вектор той же системы не зависит от выбора центра приведения и является вторым инвариантом. 21. Каков геометрический смысл второго инварианта. Что такое минимальный момент и чему он равен? Второму инварианту можно дать очень простую геометрическую интерпретацию, на основании определения скалярного произведения:
22. Как зависит главный момент системы сил от выбора центра приведения? Запишите соответствующую формулу и её формулировку. Главный момент системы сил относительно нового центра приведения Сл1: Если главный вектор данной системы сил равен нулю, то главный момент не зависит от выбора центра приведения. Сл2: Если главный вектор равен нулю и существует точка, относительно которой главный момент равен нулю, то главный момент будет равен нулю относительно любого другого центра приведения. Сл3: Главный момент данной системы сил одинаков для всех точек прямой, параллельной главному вектору.
Поиск по сайту: |
 и
и 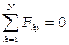 ;
; 
 и
и  и
и 
 - первый инвариант
- первый инвариант
 , откуда
, откуда таким образом, при
таким образом, при  проекция гл. момента на направление гл.вектора не зависит от выбора центра приведения. M*-проекция гл.момента на направление гл. вектора
проекция гл. момента на направление гл.вектора не зависит от выбора центра приведения. M*-проекция гл.момента на направление гл. вектора 
 равен сумме главного момента относительно старого центра приведения
равен сумме главного момента относительно старого центра приведения  и момента главного вектора относительно нового центра в предположении, что он приложен в старом центре
и момента главного вектора относительно нового центра в предположении, что он приложен в старом центре