|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Векторной форме, а также в проекциях на оси декартовой системы координатСтр 1 из 2Следующая ⇒
Сформулируйте аксиомы статики. 1-ая: Если на свободное абсолютно твёрдое тело действует две силы, то эти силы эквивалентны нулю тогда и только тогда, когда эти силы равны по модулю и направлены вдоль одной прямой в противоположные стороны. 2-ая: Действие данной системы сил на абсолютно твёрдое тело не изменится, если к ней присоединить или от неё отнять систему, эквивалентную нулю. 3-тья: Всякому действию одного материального тела на другое всегда соответствует равное по величине, но противоположно направленное противодействие. 4-ая: Две силы, приложенные к одной точке твёрдого тела, имеют равнодействующую, приложенную к той же точке и изображаемую диагональю параллелограмма, построенного на данных силах как на сторонах. 5-ая: (аксиома связей): всё то, что ограничивает свободу перемещения данного тела в пространстве, называется связью. Сила, с которой данная связь действует на тело, препятствую тем или иным его перемещениям, называется силой реакции связи, или просто реакцией связи. Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие силами реакции этих связей. 6-ая: (принцип отвердиваемости): если изменяемое (деформируемое) тело находиться под действием некоторой системы сил в равновесии, то равновесие не нарушиться и в том случае, если это тело отвердеет (т.е. станет абсолютно твёрдым). 2. Дайте определение системы сходящихся сил. Как найти равнодействующую системы сходящихся сил графическим методом? Система сил, расположенных в пространстве так, что линии из действия пересекаются в одной точке, называется системой сходящихся сил(чтобы найти равнод. Графическим методом нужно построить векторный многоугольник) 3. Дайте определение системы сходящихся сил. Как найти равнодействующую системы сходящихся сил графическим методом? Система сил, расположенных в пространстве так, что линии из действия пересекаются в одной точке, называется системой сходящихся сил(чтобы найти равнод. Графическим методом нужно построить векторный многоугольник) Дайте определение системы сходящихся сил. Как определить равнодействующую системы сходящихся сил аналитически? Система сил, расположенных в пространстве так, что линии из действия пересекаются в одной точке, называется системой сходящихся сил - Считая, что вектор силы скользящий, перенесем все силы данной системы вдоль линий действия в точку их пересечения и попарно сложим все силы методом параллелограмма. - Последовательно прикладываем вектора сил данной системы в конечную точку каждого последующего вектора, сохраняя его величину и направление, затем, соединив начало вектора 1 с концом вектора N, получим равнодействующую системы сходящихся сил. Такой метод называют методом силового много угольника. - Система сходящихся сил в общем случае эквивалентна одной силе, т.е. равнодействующей, которая приложена в точке пересечения линии действия всех сил и равна их геометрической сумме.
4. Запишите и сформулируйте условия равновесия системы сходящихся сил в векторной форме, а также в проекциях на оси декартовой системы координат. Условия равновесия в векторной форме - Для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этой системы сил равнялась нулю.
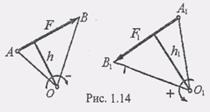
Условия равновесия в аналитической форме - - 5. Сформулируйте теорему о трех уравновешенных силах. Если под действием трёх сил тело находиться в равновесии, и линии действия двух сил пересекаются, то все силы лежат в одной плоскости и их линии действия пресекаются в одной точке. 6. Дайте определение алгебраического момента силы относительного некоторого центра. Поясните на рисунке как определить плечо силы и знак момента. Моментом силы относительно точки называется алгебраическая величина, равная произведению модуля силы на кратчайшее расстояние от точки до линии действия силы(рис1.14)
7. Сформулируйте и запишите векторное выражение момента силы относительно некоторого центра. Момент силы относительно некоторого центра равен векторному произведению радиус-вектора точки приложения силы на вектор силы.
Поиск по сайту: |
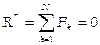 - Если
- Если 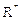 - вектор, замыкающий силовой многоугольник: геометрической условие равновесия системы сходящихся сил означает, что силовой многоугольник, построенный на векторах слагаемых сил данной системы, замкнут.
- вектор, замыкающий силовой многоугольник: геометрической условие равновесия системы сходящихся сил означает, что силовой многоугольник, построенный на векторах слагаемых сил данной системы, замкнут.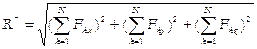 , т.е.
, т.е.  ,
, 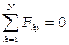 ,
,  . Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекция всех сил на каждую из трёх выбранных любым образом координатных осей равнялись нулю.
. Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекция всех сил на каждую из трёх выбранных любым образом координатных осей равнялись нулю.