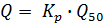|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Построение кривых обеспеченности
Годовой сток различной заданной повторяемости определяется по кривым обеспеченности. С этой целью по материалам непосредственных наблюдений строятся эмпирические кривые. Сглаживание и экстраполяция эмпирических кривых обеспеченности осуществляется графически или аналитически с использованием некоторых типовых уравнений. Графическая экстраполяция с предварительным спрямлением кривой на специальной клетчатке возможна при наличии длинного ряда наблюдений, а также, если экстраполяция незначительна. Аналитические сглаживание и экстраполяция применяется при ограниченных рядах наблюдений или при наличии длинного ряда, когда требуется перенести параметры кривой обеспеченности методом аналогии на неизученные реки. Сглаживание (выравнивание) эмпирических кривых распределения в данном случае заключается в том, что эмпирическая кривая заменяется такой теоретической кривой, моменты площади которой равны моментам площади эмпирической кривой. Сопоставление эмпирических кривых обеспеченности расходов, модулей стока с некоторыми теоретическими кривыми обеспеченности, построенными для распределения случайных величин, показали их достаточно хорошее совпадение, поэтому эти кривые используются как техническое средство для сглаживания и экстраполяции эмпирических кривых до заданных пределов обеспеченности. Для построения теоретической кривой обеспеченности, которая бы соответствовала эмпирической кривой, необходимо по данным наблюдения вычислить значения параметров ее дифференциального уравнения и произвести его интегрирование. Параметрами теоретических кривых обеспеченности являются: 1) средне многолетняя величина, норма, годового стока (Qо, Мо); 2) коэффициент вариации, изменчивости годового стока (Cv); 3) коэффициент асимметрии годового стока (Cs). Определить параметры теоретической кривой по методу моментов (табл.2). Таблица 2 Расчет параметров методом моментов
Найти значение средне арифметического ряда наблюдений, значение среднеквадратического отклонения. По данным расчетов определить коэффициент вариации (формула 2.2 и 2.3). Для ранжированного ряда рассчитать значения модульного коэффициента обеспеченности k ( Определить значение коэффициента асимметрии Cs (формула 2.8). 2. Рассчитать параметры теоретической кривой по методу наибольшего правдоподобия. Составить таблицу (табл. 3) для расчетов параметров по методу наибольшего правдоподобия.
Таблица 3 Расчет параметров методом наибольшего правдоподобия
Вычислить статистики l2 и l3
По значениям статистик l2 и l3 по графикам (Приложения 2) найти значения Cv и Cs . По соотношению Cv и Cs по таблице (Приложение 1) определить значения вероятности Р % для 1, 5, 10, 50, 80, 95, 99 % обеспеченности и построить кривую на клетчатке вероятности. В таблицах часто значения вероятностей даются для дискретных значений Cs, Cv, то значения Фр% для нужного значения Cs можно найти методом интерполяции, например, Cs равно 0,25, а имеются значения 0, и 0,3. Тогда берем значения отклонений для Cs 0,2 и 0,3, например, 3,33 (0,1% обеспеченности) и 3,52. Для значения Cs = 0,25 нормируемое отклонение составит (3,52 – 3,33): 2 = 3,43. Рассчитать параметры теоретической кривой графоаналитическим методом. Вычисляют эмпирическую обеспеченность Р каждого члена статистического ряда по формуле
где m - порядковый номер ранжированного ряда, n - число членов ряда. С графика эмпирической кривой распределения снять координаты при значениях вероятности 5%, 50%, 95%. Значения расходов берутся из убывающего ряда для соответствующего значения вероятности. Например, при числе лет наблюдений накопленные вероятности ( Легко заметить, что между 1-м и 2-м членами убывающего ряда расположится значение 5% обеспеченности. Точное значение расхода эмпирической обеспеченности получим путем интерполяции значений признака (расхода). Аналогично поступают и при вычислении значений признака, соответствующих обеспеченности 50% и 95%. На специальной клетчатке построить эмпирическую кривую распределения модульного коэффициента обеспеченности. Рассчитать значения коэффициента скошенности S
В таблице нормированных отклонений значения S размещены в крайнем правом столбце. Проведя прямую линию по строке таблицы, увидим значения Cs (Приложение 1), кроме того, в предпоследнем столбце этой же таблицы снимают показания разности (Ф5 – Ф95) определить значение коэффициента асимметрии Cs. Определить значения среднеквадратического отклонения s и среднего значения модульного коэффициента k (формула 2.9). Формула 2.4 легко может быть преобразована, путем замены значений признака на Составить таблицу для вычисления ординат теоретической кривой (табл.4).
Таблица 4 Вычисление ординат теоретической кривой обеспеченности графо-аналитическим методом
Проверить допустимость метода. Из построенных теоретических кривых подобрать кривую наилучшим образом подходящую к эмпирической кривой. При этом следует обращать внимание на сходимость теоретических и эмпирических значений на концах эмпирической кривой.
3.3. Определение расходов в реке при отсутствии данных наблюдений расходов (По картам ГГИ).
Расчет производится с использованием формулы
где М0 – модуль стока для реки данного района, л/с×км2. Определяется по картам ГГИ или картам местного Центра Гидрометеослужбы, F – площадь водосбора, км2.
М0 = 4,5 л/с×км2;
По картам ГГИ определяются значения коэффициентов вариации Сv и коэффициентов асимметрии Сs. Для этого на карте определяют район расположения бассейна реки и рекомендуемое значение Cv, затем по району расположения бассейна определяют соотношение Cs / Cv. Например, Cv = 0,25, соотношение Cs / Cv = 3, т.е. Cs = 0,75. По значению Cs в таблице нормированных отклонений от среднего значения ординат биномиальной кривой обеспеченности выписывается ряд значений Ф (Р, Cs). Затем по формуле Расход воды в реке различной обеспеченности Qp определяют умножением значений Q0 на значения Кр. Данные расчета представить в виде таблицы и графика теоретической кривой на клетчатке с умеренной асимметричностью (кривая 1). Расчет параметров теоретической кривой р. Волоть представлен в таблице. Таблица 5.
Поиск по сайту: |
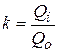
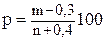

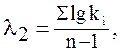
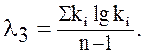 .
.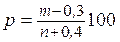 %,
%,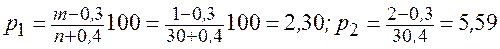 и т.д.
и т.д. .
.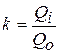 ). Найти значения Qo и Cv. Значение среднего Qo можно получить, преобразовав модульный коэффициент, т.е. Q0 = k×Qp%. По формуле (2.4) определить значение Cv..
). Найти значения Qo и Cv. Значение среднего Qo можно получить, преобразовав модульный коэффициент, т.е. Q0 = k×Qp%. По формуле (2.4) определить значение Cv..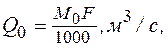 (2.10)
(2.10)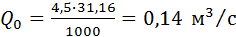
 определяют ряд значений модульных коэффициентов различной обеспеченности.
определяют ряд значений модульных коэффициентов различной обеспеченности.