 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Статистические методы при гидрологических исследованиях
В гидрологических исследованиях и расчетах расходы воды в реке являются главной характеристикой речного стока. Наряду с экстремальными значениями расходов воды (max, min) часто используются расходы воды, осредненные за различные периоды времени (сутки, месяц, сезон, год). Порядок определения наиболее часто употребляемых гидрологических характеристик установлен нормативными документами и СНиПами. Расход воды в реке устанавливают в зависимости от наличия или отсутствия наблюдений за водным режимом реки. При наличии ряда наблюдений устанавливаются следующие характеристики: среднее арифметическое значение расхода, среднеквадратическое отклонение, коэффициенты вариации и асимметрии. Для вычисления среднего расхода весь ряд наблюдений разделяется на интервалы шириной
где Qmax , Qmin – максимальное и минимальное значение расходов в ряде наблюдений. Ряд наблюдений разделяется на число интервалов
Начиная с первого значения, определяют число событий (попаданий) в полученные значения интервалов (заполняется колонка 3 нижеследующей таблице). Для расчетов строим таблицу: Таблица 1
Средне арифметическая величина статистического ряда, может быть определена по формуле:
где
Среднеквадратическое отклонение единичных значений годового стока
При числе лет наблюдения меньше 30 в приведенное для среднеквадратического отклонения выражение подставляется (n – 1) лет. Мерой изменчивости той или иной величины является коэффициент Cv вариации, который представляет собой отношение среднеквадратического отклонения к среднему значению ряда:
В качестве характеристики асимметричности ряда принимается среднее значение отклонений членов ряда от его средне арифметического значения в третьей степени
В симметричных распределениях отклонения от среднего взаимно уравновешиваются, поэтому m3 равно нулю. Коэффициент асимметрии определяют по формуле
Поиск по сайту: |

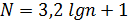
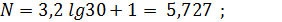
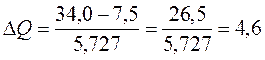 .
.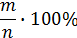

 , м3/с,
, м3/с,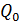 – норма годового стока,
– норма годового стока, 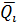 – середина интервала.
– середина интервала.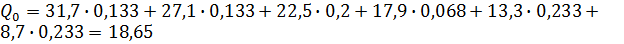 м3/с.
м3/с. м3/с
м3/с от среднего за n лет определяется по следующей формуле:
от среднего за n лет определяется по следующей формуле:
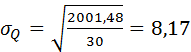
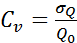 ,
,  =0,4
=0,4 ,
,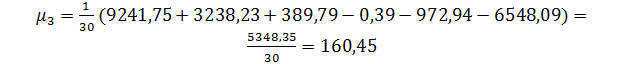
 ,
, 