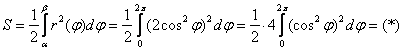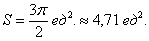|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Метод решения несобственного интеграла с бесконечным нижним пределом
Второй раздел статьи предназначен для тех, кто хорошо разобрался с урокомНесобственные интегралы. Примеры решения, или, по крайне мере, понял бОльшую его часть. Речь пойдет о несобственных интегралах первого рода с бесконечным нижним пределом: Пример 7 Вычислить несобственный интеграл или установить его расходимость. Чем отличается данный интеграл от «обычного» несобственного интеграла с бесконечным верхним пределом? По технике решения практически ничем. Так же нужно найти первообразную (неопределенный интеграл), так же нужно использовать предел при вычислении интеграла. Отличие состоит в том, что необходимо устремить нижний предел интегрирования к «минус бесконечности»: Из вышесказанного следует очевидная формула для вычисления такого несобственного интеграла: В данном примере, подынтегральная функция непрерывна на Вот тут, главное, быть аккуратным в знаках, и не забывать, что Пример 8 Вычислить несобственный интеграл или установить его расходимость. Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Метод решения несобственного интеграла Очень интересный случай. Несобственный интеграл первого рода с бесконечными пределами интегрирования имеет следующий вид: Как решить интеграл с бесконечными пределами? Данный интеграл нужно представить в виде суммы двух несобственных интегралов: Если оба интеграла правой части сходятся, то сходится и интеграл Пример 9 Вычислить несобственный интеграл или установить его расходимость.
Я специально подобрал примитивный пример, чтобы проиллюстрировать другой важный момент применения метода. Подынтегральная функция непрерывна на всей числовой прямой. Интеграл будет сходиться, если будут сходиться оба интеграла правой части.
Оба интеграла сходятся, значит, сходится и весь интеграл: Теперь обратим внимание на подынтегральную функцию. Она является чётной. То есть, решение допустимо записать короче: Почему такое возможно? График подынтегральной чётной функции симметричен относительно оси Пример 10 Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция непрерывна на всей числовой прямой. Согласно правилу, интеграл нужно представить в виде суммы двух интегралов: Проверяем сходимость интегралов правой части: Не нужно проверять сходимость второго интеграла правой части, поскольку для того, чтобы интеграл Ответ: несобственный интеграл А сейчас очень важный момент: подынтегральная функция В этом состоит отличие от определенного интеграла. Там всегда можно смело записать: Тонкость же состоит в том, что несобственный интеграл Как раз этой тонкости посвящен следующий пример для самостоятельного решения: Пример 11 Вычислить несобственный интеграл или установить его расходимость.
Полное решение и ответ в конце урока.
Метод решения несобственного интеграла второго рода Заключительные пункты этой статьи предназначены для читателей, которые хорошо разобрались с несобственными интегралами второго рода на уроке Несобственные интегралы. Примеры решений. Рассмотрим другие разновидности несобственных интегралов второго рода. Ничего сложного! Многие выкладки предыдущего параграфа будет справедливы и сейчас. Сразу конкретная задача: Пример 12 Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечные разрывы в обоих концах отрезка интегрирования. Изобразим подынтегральную функцию Геометрически данный несобственный интеграл представляет собой площадь бесконечной криволинейной трапеции, которая не ограничена сверху. Методика решения практически такая же, как и в предыдущем параграфе. Представим несобственный интеграл в виде суммы двух несобственных интегралов:
Если оба интеграла правой части сходятся, то сходится и весь интеграл. А уж интегралы правой части рассматривались во втором разделе урока Несобственные интегралы. Примеры решений. Но, вместо этого замечаем, что подынтегральная функция является чётной. Чётность использовать МОЖНО. В этом легко убедиться и по чертежу. Таким образом, интеграл целесообразно споловинить, а результат удвоить. Решаем наиболее рациональным способом: Подынтегральная функция терпит бесконечные разрывы в точках
Ответ: Пример 13 Вычислить несобственный интеграл или установить его расходимость.
Это пример для самостоятельного решения. Всё, как и в предыдущем параграфе –нечетностью функции пользоваться НЕ НУЖНО. Аккуратно делим интеграл на две части и исследуем сходимость по типовому алгоритму. Полное решение и ответ в конце урока. Не редкость, когда подынтегральная функция не является четной или нечетной, да и отрезок интегрирования не симметричен относительно нуля. Например, рассмотрим несобственный интеграл Таки удобное свойство, правда? Интегралы правой части разобраны на уроке Несобственные интегралы. Примеры решений. Если оба интеграла будут сходиться, то будет сходиться и весь интеграл. Еслихотя бы один интеграл правой части расходится, то расходится и весь интеграл. Кстати, не важно, в каком порядке исследовать сходимость интегралов правой части. Можно сначала исследовать сходимость интеграла
Метод решения несобственного интеграла Если честно, такой пример встречался в моей практике всего один раз (по крайне мне, вспомнил лишь один), поэтому я ограничусь только обзором. Пример опять же будет в известной степени условным, первое, что в голову пришло. Рассмотрим несобственный интеграл Метод уже состарился, как хмм… чешуя динозавра. Представим несобственный интеграл в виде суммы двух несобственных интегралов: Интегралы правой части вам уже знакомы. А проговаривать алгоритм в третий раз не буду, смотрите предыдущие два параграфа) Желаю успехов! Решения и ответы: Пример 2: Решение: Пример 5: Решение: Пример 8: Решение: Пример 11: Решение: Пример 13: Решение: Интеграл Автор: Емелин Александр
Высшая математика для заочников и не только >>> (Переход на главную страницу) Как можно отблагодарить автора?
Это, пожалуй, одно из самых популярных приложений определённого интеграла после вычисления площади в прямоугольных координатах и объёма тела вращения. Для изучения материалов урока необходимо понимать, что такое полярные координаты и знать полярные уравнения простейших линий. Разумеется, потребуются навыки нахождениянеопределённого и определённого интеграла, поэтому если у вас появятся технические трудности и/или недопонимание по ходу изложения, пожалуйста, начните с базовых статей. Всё очень и очень напоминает привычную задачу нахождения площади. Полярным аналогом криволинейной трапеции является криволинейный сектор. Рассмотрим некоторую функцию В качестве демонстрационного примера, вычислим площадь круга, ограниченного окружностью Сравните с Примером №4 урока Эффективные методы решения определённых интегралов, где площадь этого же круга рассчитана в прямоугольной системе координат ;-) Бензопила заправлена и прогрета: Пример 1 Вычислить площадь фигуры, ограниченной линией Решение: первый и главный совет: Экономьте время на чертеже. Проще всего прибегнуть к программным средствам, например, воспользоваться моим графопостроителем в полярных координатах. Клик-клик – и готово, далее быстренько перерисовываем чертёж в тетрадь или при электронном способе оформления копируем его в Вёрд. Если есть возможность быстро построить фигуру – всегда её стройте (даже если этого не требуется по условию). Чертёж усиливает задание, кроме того, как и при нахождении площади в прямоугольных координатах, даёт отличную возможность прикинуть по клеточкам правдоподобность получившегося результата. Если же инструментальные средства по той или иной причине недоступны, и вы совсем не представляете, как выглядит фигура, то придерживайтесь противоположной тактики: По возможности чертёж выгоднее НЕ строить вообще. Ручное построение чертежа в полярных координатах – процесс длительный и трудоёмкий, за это время можно успеть В нашем случае задача облегчается ещё и тем, что
Стандартнопонижаем степень с помощью известной тригонометрической формулы:
Ничего сложного тут нет, главное, не допустить ошибку в преобразованиях и вычислениях. Ответ: Забавно, что можно вообще не иметь ни малейшего представления о том, какую фигуру ограничевает линия
Поиск по сайту: |
 .
.
 .
.
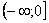 и:
и: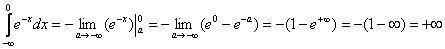 , то есть, несобственный интеграл расходится.
, то есть, несобственный интеграл расходится.

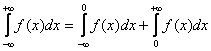
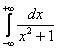
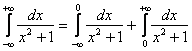
 – сходится.
– сходится. – сходится.
– сходится.
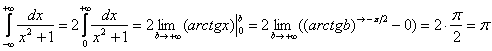
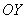 . Следовательно, если половина площади конечна (интеграл сходится) – то симметричная половина площади тоже конечна. Если половина площади бесконечна (интеграл расходится), следовательно, симметричная половина тоже будет расходиться.
. Следовательно, если половина площади конечна (интеграл сходится) – то симметричная половина площади тоже конечна. Если половина площади бесконечна (интеграл расходится), следовательно, симметричная половина тоже будет расходиться.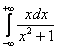

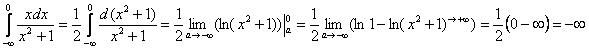
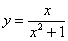 является нечётной. В несобственных интегралах с бесконечными пределами (а значит, симметричными интервалами интегрирования) нечётностью пользоваться НЕ СЛЕДУЕТ!!!
является нечётной. В несобственных интегралах с бесконечными пределами (а значит, симметричными интервалами интегрирования) нечётностью пользоваться НЕ СЛЕДУЕТ!!!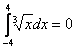 , а здесь так поступать – не следует. Почему? Потому что в ряде случаев, как, например, в рассмотренном примере, получится нонсенс. Если считать, что
, а здесь так поступать – не следует. Почему? Потому что в ряде случаев, как, например, в рассмотренном примере, получится нонсенс. Если считать, что  , то интеграл будет сходящимся (поскольку получено конечное число), но в то же время его часть:
, то интеграл будет сходящимся (поскольку получено конечное число), но в то же время его часть:  – расходится (как мы только что показали в решении).
– расходится (как мы только что показали в решении).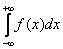 от нечетной функции
от нечетной функции 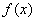 , в принципе, может равняться нулю, но нельзя сразу записывать, что
, в принципе, может равняться нулю, но нельзя сразу записывать, что  . Всегда представляем интеграл в виде двух интегралов и выполняем проверку на сходимость по стандартному алгоритму.
. Всегда представляем интеграл в виде двух интегралов и выполняем проверку на сходимость по стандартному алгоритму.

 на чертёже:
на чертёже:
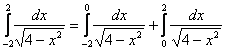

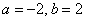 . Данная функция является чётной, а интервал интегрирования симметричен относительно нуля.
. Данная функция является чётной, а интервал интегрирования симметричен относительно нуля.
 , то есть, несобственный интеграл сходится
, то есть, несобственный интеграл сходится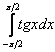
 . Подынтегральная функция опять терпит бесконечные разрывы в обоих концах отрезка интегрирования. Алгоритм такой же, делим интеграл на два интеграла:
. Подынтегральная функция опять терпит бесконечные разрывы в обоих концах отрезка интегрирования. Алгоритм такой же, делим интеграл на два интеграла:
 , а потом (если до этого дойдет дело), исследовать сходимость интеграла
, а потом (если до этого дойдет дело), исследовать сходимость интеграла  .
. . На концах отрезка интегрирования всё хорошо. Но подынтегральная функция терпит бесконечный разрыв прямо на отрезке в точке
. На концах отрезка интегрирования всё хорошо. Но подынтегральная функция терпит бесконечный разрыв прямо на отрезке в точке 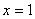 . Подынтегральная функция является четной, но это не имеет никакого значения, поскольку отрезок интегрирования не симметричен относительно нуля.
. Подынтегральная функция является четной, но это не имеет никакого значения, поскольку отрезок интегрирования не симметричен относительно нуля.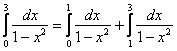
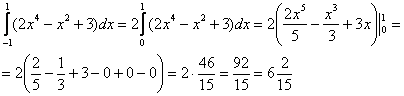

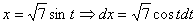

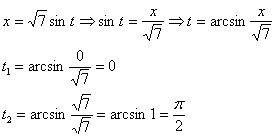

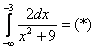

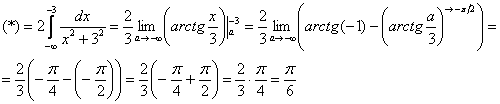


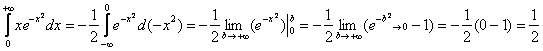
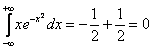

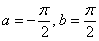 .
. 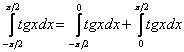

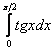 можно уже не проверять.
можно уже не проверять.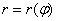 , заданную в полярной системе координат,которая принимает неотрицательные значения на отрезке
, заданную в полярной системе координат,которая принимает неотрицательные значения на отрезке  и непрерывна на нём.Криволинейным сектором называется ФИГУРА, ограниченная отрезками лучей
и непрерывна на нём.Криволинейным сектором называется ФИГУРА, ограниченная отрезками лучей 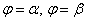 и графиком
и графиком 
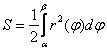 . Как видите, перед интегралом ставится дробь
. Как видите, перед интегралом ставится дробь  , сама функция
, сама функция  возводится в квадрат, а интегрирование осуществляется по переменной «фи».
возводится в квадрат, а интегрирование осуществляется по переменной «фи». с центром в полюсе, радиуса 2. Очевидно, что
с центром в полюсе, радиуса 2. Очевидно, что 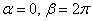 и по формуле:
и по формуле: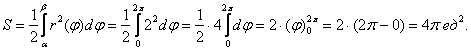
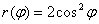
 для любого «фи»,
для любого «фи»,  до
до  . По рабочей формуле:
. По рабочей формуле: