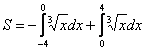|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Несобственные интегралы от неограниченных функций
Иногда такие несобственные интегралы называют несобственными интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: Если подынтегральной функции не существует в точке Сразу пример, чтобы было понятно: Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования. В этой связи проверим и верхний предел: Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:
Здесь почти всё так же, как в интеграле первого рода. Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению Посмотрим, как это реализуется на практике. Пример 6 Вычислить несобственный интеграл или установить его расходимость. Подынтегральная функция терпит бесконечный разрыв в точке Сначала вычислим неопределенный интеграл: Замена:
У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле. Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: (2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница. (3) Разбираемся с В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью А сейчас два примера для самостоятельного решения. Пример 7 Вычислить несобственный интеграл или установить его расходимость. Пример 8 Вычислить несобственный интеграл или установить его расходимость. Если подынтегральной функции не существует в точке Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом:
Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению Пример 9 Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке Для разнообразия я решу этот интеграл сразу – методом подведения функции под знак дифференциала. Те, кому трудно, могут сначала найти неопределенный интеграл по уже рассмотренной схеме.
Добавка Разбираемся, почему дробь Окончательно: Несобственный интеграл расходится. Знак минус обозначает, что соответствующая криволинейная трапеция расположена под осью И заключительные два примера для самостоятельного рассмотрения: Пример 10 Вычислить несобственный интеграл или установить его расходимость.
Пример 11 Вычислить несобственный интеграл или установить его расходимость.
Разбор ситуации, когда оба предела интегрирования «плохие», или точка разрыва содержится прямо на отрезке интегрирования, можно найти в статье Эффективные методы решения несобственных интегралов. Желаю успехов! Решения и ответы: Пример 4: Решение: Пример 7: Решение: Примечание: с пределом выражения Пример 8: Решение: Примечание: Разбираемся в пределе выражения Пример 10: Решение: Пример 11: Решение: Примечание: Разбираемся в пределе выражения Автор: Емелин Александр
Высшая математика для заочников и не только >>> (Переход на главную страницу) Как можно отблагодарить автора?
Данная статья содержит дополнительные материалы по методам решения определенных и несобственных интегралов. Предполагается, что читатель владеет средними или высокими навыки интегрирования. Если это не так, пожалуйста, начните с азов, предназначенных для чайников: Неопределенный интеграл, примеры решений. Где неопределенный интеграл – там неподалёку и Определенный интеграл, с формулой Ньютона-Лейбница вы тоже должны быть знакомы не понаслышке. Кроме того, уметь решать простейшие задачи на вычисление площади плоской фигуры. Урок предназначен для тех, кто хочет научиться быстрее и эффективнее решать определенные и несобственные интегралы. Сначала я рассмотрю особенности интегрирования четной и нечетной функции по симметричному относительно нуля интервалу. Затем мы разберем задачу о нахождении площади круга с помощью определенного интеграла. Эта задача важна еще и тем, что знакомит вас с распространенным приемом интегрирования определенного интеграла – тригонометрической подстановкой. Она еще нигде не рассматривалась – новый материал! Второй раздел предназначен для читателей, знакомых с несобственными интегралами. Аналогично, рассмотрим несобственные интегралы от четных, нечетных функций по симметричному интервалу. В том числе более редкие типы несобственных интегралов, которые не вошли в основную статью: когда нижний предел стремится к «минус бесконечности», когда оба предела стремятся к бесконечности, когда в обоих концах отрезка интегрирования функция терпит бесконечный разрыв (это уже интеграл второго рода). И совсем редкий несобственный интеграл – сточкой разрыва на отрезке интегрирования.
Метод решения определенного интеграла от четной функции Рассмотрим определенный интеграл вида Если функция подынтегральная Многие догадались, почему так, тем не менее, рассмотрим конкретный пример с чертежом: Пример 1 Вычислить определенный интеграл В данном случае: Согласно правилу, на симметричном относительно нуля отрезке А сейчас геометрическая интерпретация. Да, продолжаем мучить несчастную параболу…. Любая чётная функция, в частности Определенный интеграл Аналогичная история происходит с любой чётной функцией Некоторые скажут: «Да зачем это всё нужно, можно ведь и так вычислить определенный интеграл». Можно. Давайте вычислим: Но удобно ли было подставлять отрицательный нижний предел? Не очень-то. Кстати, ненулевой процент студентов допустит ошибку в знаках. Гораздо проще и приятнее подставить ноль. Замечу, что это еще был простой демонстрационный пример, на практике всё бывает хуже. Кроме того, рассматриваемый прием часто применяется при вычислении двойных интегралов, тройных интегралов, где вычислений и так хватает. Короткий разминочный пример для самостоятельного решения: Пример 2 Вычислить определенный интеграл Полное решение и ответ в конце урока. Обратите внимание, что когда вам предложено просто вычислить определенный интеграл, то чертеж выполнять не нужно! Иллюстрация к Примеру 1 дана только для того, чтобы было понятно правило. Как раз данному моменту посвящена следующая простая задачка: Пример 3 1) Вычислить определенный интеграл Это две разные задачи!Об этом уже говорилось в статье Как вычислить площадь плоской фигуры? Сначала разберемся с первым пунктом: 1) Подынтегральная функция является чётной, отрезок интегрирования симметричен относительно нуля, поэтому: Определенный интеграл получился отрицательным и так бывает! 2) Теперь найдем площадь плоской фигуры. Вот здесь без чертежа обойтись трудно: Если у вас возникло затруднение с наивным косинусом, пожалуйста, обратитесь к статьеГеометрические преобразования графиков. На отрезке Площадь не может быть отрицательной, именно поэтому в формуле вычисления площади добавляют минус (также см. пример 3 урока Определенный интеграл. Как вычислить площадь фигуры). Заметьте, что чётность косинуса никто не отменял, поэтому мы опять споловинили отрезок, и удвоили интеграл.
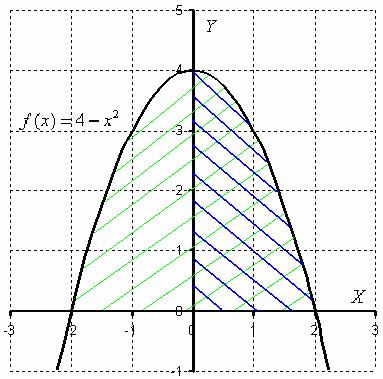
Вычисление площади круга с помощью определенного интеграла Это очень важная задача, поскольку будет рассмотрен типовой интеграл и приём решения, который неоднократно встретится в будущем. Но сначала небольшое напоминание по уравнению окружности. Уравнение вида Пример 4 Вычислить площадь круга, ограниченного окружностью, заданной уравнением
Выполним чертёж: Сначала вычислим площадь круга с помощью известной школьной формулы. Если радиус круга Для того чтобы вычислить площадь круга с помощью определенного интеграла, необходимо из уравнения окружности Верхняя полуокружность задается уравнением Особые параноики, как я, могут подставить несколько точек окружности в эти уравнения, и убедиться в справедливости вышеизложенных утверждений. Как вычислить площадь круга? В данном примере круг симметричен относительно начала координат, поэтому достаточно вычислить площадь сектора в 1-ой четверти (заштрихован синим цветом), затем результат умножить на 4. Таким образом: Такой же, но неопределенный интеграл рассматривался в примере 6 урока Сложные интегралы, он решался длительным и трудоёмким методом сведения интеграла к самому себе. Можно пойти тем же путём, но для определенного интеграла существует удобный и эффективный метод тригонометрической замены: Проведём замену: Почему именно такая замена, очень скоро станет понятно, а пока найдем дифференциал: Выясним, во что превратится корень, я распишу очень подробно: Если в ходе решения вы не сможете догадаться применить формулу наподобие После преобразования корня отчетливо видно, почему проведена замена Осталось вычислить новые пределы интегрирования: Новый нижний предел интегрирования: Таким образом: Площадь сектора необходимо умножить на 4, следовательно, площадь всей окружности: Вероятно, у некоторых возник вопрос, зачем вообще мучиться с интегралом, если есть короткая школьная формула Разобранный пример можно решить в общем виде, то есть найти площадь круга, ограниченного окружностью произвольного радиуса: Следует отметить, что к решению данной задачи можно было применить и другой подход – вычислить площадь верхнего полукруга с помощью интеграла Еще раз подчёркиваю важность проведенной тригонометрической замены, она встретится на практике ни раз и ни два. Поэтому для закрепления материала чуть более сложное задание для самостоятельного решения: Пример 5 Вычислить определенный интеграл По условию требуется вычислить определенный интеграл, поэтому чертеж выполнять не нужно. Хорошо подумайте над коэффициентом в замене
Метод решения определенного интеграла от нечетной функции Вам понравится. Рассмотрим тот же определенный интеграл с симметричным относительно нуля отрезком интегрирования: Почему такой интеграл равен нулю? Пример 6 Вычислить определенный интеграл Выполним чертеж: Вот, заодно и график функции Проверим нашу функцию на четность/нечетность: При вычислении определенного интеграла И еще раз подчеркиваю разницу между заданиями: 1) Любой определенный интеграл (само собой он должен существовать) – это всё равно формально площадь (пусть даже отрицательная). В частности, поэтому 2) Задача на нахождение площади – это совершенно другая задача. Так, если бы нам было предложено найти площадь фигуры в данном примере, то её следовало бы вычислить следующим образом: Еще несколько коротких примеров на тему данного правила: И, аналогично для любой нечетной функции и симметричного относительно нуля отрезка. Применять ли данный метод на практике? На самом деле вопрос не такой простой. Когда вам предложен сложный пример с большим количеством вычислений, то можно, и даже уместно указать, что такой интеграл равен нулю, сославшись на нечетность функции и симметричность отрезка интегрирования относительно нуля. Как говорится, знание – сила, а незнание – рабочая сила. Но когда вам предложен короткий пример, то преподаватель вполне обоснованно может заставить прорешать его подробно: взять интеграл и подставить пределы интегрирования по формуле Ньютона-Лейбница. Например, вам предложено вычислить тот же определенный интеграл
Поиск по сайту: |
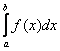 . Но, в отличие от определенного интеграла, подынтегральная функция
. Но, в отличие от определенного интеграла, подынтегральная функция 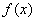 терпит бесконечный разрыв (не существует): 1) в точке
терпит бесконечный разрыв (не существует): 1) в точке  , 2) или в точке
, 2) или в точке  , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.
, 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок. . Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела
. Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела  , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
, то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке! . Здесь всё хорошо.
. Здесь всё хорошо.
 справа.Легко проследить по чертежу: по оси
справа.Легко проследить по чертежу: по оси  мы должны бесконечно близко приблизиться к точке разрыва справа.
мы должны бесконечно близко приблизиться к точке разрыва справа. (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)
(не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)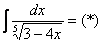



 . Добавка
. Добавка  обозначает, что мы стремимся к значению
обозначает, что мы стремимся к значению  справа (что логично – см. график). Такой предел в теории пределов называютодносторонним пределом. В данном случае у нас правосторонний предел.
справа (что логично – см. график). Такой предел в теории пределов называютодносторонним пределом. В данном случае у нас правосторонний предел. при
при  . Причесываем ответ.
. Причесываем ответ.
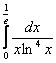


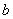 слева. По оси
слева. По оси 
 (устно проверяем, что с другим пределом интегрирования всё нормально!).
(устно проверяем, что с другим пределом интегрирования всё нормально!).
 обозначает, что предел у нас левосторонний, и к точке
обозначает, что предел у нас левосторонний, и к точке  (это лучше делать устно или на черновике).
(это лучше делать устно или на черновике). :
: 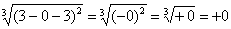 и тогда
и тогда 

 и
и  – это разные вещи, разные жанры, и если Вы недосмотрите за знаками, то, строго говоря, допустите серьезную ошибку.
– это разные вещи, разные жанры, и если Вы недосмотрите за знаками, то, строго говоря, допустите серьезную ошибку.


 .
.

 .
.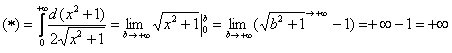


 можно разобраться следующим образом: вместо
можно разобраться следующим образом: вместо  :
: 



 . Если
. Если  , то
, то  (см. график логарифмической функции!), тогда:
(см. график логарифмической функции!), тогда: 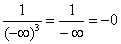 . Именно эти соображения и помечаются как
. Именно эти соображения и помечаются как 


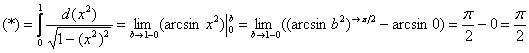

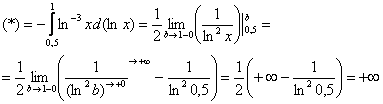
 . Если
. Если  , то
, то  , и тогда
, и тогда 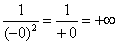 . Будьте очень внимательны в знаках!
. Будьте очень внимательны в знаках! . Легко заметить, что отрезок интегрирования
. Легко заметить, что отрезок интегрирования 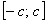 симметричен относительно нуля.
симметричен относительно нуля. .
.
 . Как проверить функцию на чётность? Нужно вместо«икс» подставить
. Как проверить функцию на чётность? Нужно вместо«икс» подставить  .
.
 , значит, данная функция является чётной.
, значит, данная функция является чётной. наш интеграл от чётной функции можно вычислить следующим образом:
наш интеграл от чётной функции можно вычислить следующим образом:
 :
:




 .
. и осью
и осью  .
.

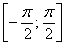 график функции расположен ниже оси
график функции расположен ниже оси 
 задаёт окружность с центром в точке
задаёт окружность с центром в точке  радиуса
радиуса  . В частности, уравнение
. В частности, уравнение 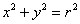 задаёт окружность радиуса
задаёт окружность радиуса 
 – это окружность с центром в начале координат радиуса
– это окружность с центром в начале координат радиуса  .
.


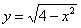





 , то, увы, схлопочете от преподавателя «приходите в следующий раз».
, то, увы, схлопочете от преподавателя «приходите в следующий раз».
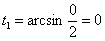



 ? А фишка состоит в том, что возможность очень точно вычислить площадь круга появилась только с развитием математического анализа (хотя уже в древности площадь круга рассчитывали с приличной точностью).
? А фишка состоит в том, что возможность очень точно вычислить площадь круга появилась только с развитием математического анализа (хотя уже в древности площадь круга рассчитывали с приличной точностью). , а затем удвоить результат. Но в силу чётности подынтегральной функции решение элементарно сводится к оптимальной версии:
, а затем удвоить результат. Но в силу чётности подынтегральной функции решение элементарно сводится к оптимальной версии:

 . Если возникнут трудности с интегралом после замены, вернитесь к уроку Интегралы от тригонометрических функций. Будьте внимательны! Полное решение и ответ в конце урока.
. Если возникнут трудности с интегралом после замены, вернитесь к уроку Интегралы от тригонометрических функций. Будьте внимательны! Полное решение и ответ в конце урока. .
.

 , который ещё нигде у меня не встречался, график представляет собой перевёрнутую кубическую параболу.
, который ещё нигде у меня не встречался, график представляет собой перевёрнутую кубическую параболу.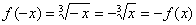 , значит, данная функция является нечётной, и её график симметричен относительно начала координат. Из симметрии графика следует равенство площадей, которые заштрихованы красным и синим цветом.
, значит, данная функция является нечётной, и её график симметричен относительно начала координат. Из симметрии графика следует равенство площадей, которые заштрихованы красным и синим цветом.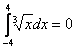 .
.