 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Рассмотрим основные свойства определённого интеграла
У меня нет цели копипастить учебники, и я остановлюсь только на тех свойствах, которые имеют существенное значение для практики. Нумерация, пожалуй, ни к чему: – Свойство, которое уже фигурировало в предыдущем пункте: интеграл с одинаковыми пределами интегрирования равен нулю: – Свойства линейности: – Если у интеграла поменять местами пределы интегрирования, то он сменит знак: Почему? Пусть для определённости Следует заметить, что на практике намного чаще пользуются вторым случаем – когда изначально – Какими бы ни были точки Здесь в первую очередь, конечно же, напрашивается ситуация, когда точка «цэ» лежит внутри отрезка Но данное свойство работает и в «нестандартном» случае, когда точка «цэ» лежит вне промежутка – Пожалуйста, запомните! Если подынтегральная функция Свойство элементарно доказывается: снова вспоминаем, что Таким образом, если при вычислении интеграла Наоборот – если интеграл ! Совет: перед решением любого определённого интеграла всегда полезно проанализировать знак подынтегральной функции! –Ещё одно важное свойство. Если функции Тоже всё наглядно – график функции Из данного свойства следует важнейшая рабочая формула вычисления площади фигуры, ограниченной графиками функций – Если Рассмотрим конкретную задачу, поясняющую геометрический смысл данного свойства, а то я чувствую, вы уже изнываете без практики =) Пример 1 Оценить определенный интеграл Решение: подынтегральная функция 1) Вычислим значения функции в критических точках, принадлежащих отрезку: 2) Вычислим значения функции на концах отрезка: Таким образом: Длина отрезка интегрирования: В результате, оценка определённого интеграла: Ответ: Геометрически это означает, что площадь – И в заключение параграфа – теорема о среднем: если функция Доказательство опустим, поскольку в нём фигурируют другие теоремы математического анализа. А сейчас оставшихся со мной читателей ждёт вознаграждение, позволяющее проникнуться, если хотите, философией темы:
Поиск по сайту: |
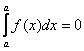 . Графическая интерпретация очевидна: криволинейная трапеция вырождается в отрезок, а площадь отрезка с геометрической точки зрения равна нулю.
. Графическая интерпретация очевидна: криволинейная трапеция вырождается в отрезок, а площадь отрезка с геометрической точки зрения равна нулю.

 . Тогда при перестановке пределов интегрирования разбиение отрезка
. Тогда при перестановке пределов интегрирования разбиение отрезка 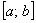 будет проводиться справа налево (вспоминаем ступенчатую фигуру 1-го чертёжа), и длины частичных промежутков формально станут отрицательными
будет проводиться справа налево (вспоминаем ступенчатую фигуру 1-го чертёжа), и длины частичных промежутков формально станут отрицательными  , поэтому интегральная сумма
, поэтому интегральная сумма  и сам интеграл (как предел суммы) сменит знак.
и сам интеграл (как предел суммы) сменит знак. , например:
, например:
 и так рассчитывается без всяких проблем. Однако не редкость, когда перестановка пределов интегрирования не только удобна, но и рациональна.
и так рассчитывается без всяких проблем. Однако не редкость, когда перестановка пределов интегрирования не только удобна, но и рациональна. :
:
 , то
, то  (здесь и далее полагаем, что
(здесь и далее полагаем, что  , то интеграл будет неположительным:
, то интеграл будет неположительным:  .
. . Длины частичных промежутков положительны:
. Длины частичных промежутков положительны:  , но в первом случае значения функции
, но в первом случае значения функции  (криволинейная трапеция лежит не ниже оси абсцисс), а во втором случае
(криволинейная трапеция лежит не ниже оси абсцисс), а во втором случае  (криволинейная трапеция лежит не выше оси абсцисс)
(криволинейная трапеция лежит не выше оси абсцисс) у вас получилось отрицательное значение – ищите ошибку. Функция
у вас получилось отрицательное значение – ищите ошибку. Функция  на промежутке интегрирования
на промежутке интегрирования  (и, к слову, вообще на любом ненулевом промежутке), поэтому интеграл
(и, к слову, вообще на любом ненулевом промежутке), поэтому интеграл  получился положительным, то здесь тоже где-то допущена ошибка, поскольку
получился положительным, то здесь тоже где-то допущена ошибка, поскольку  на отрезке
на отрезке  .
. интегрируемы на
интегрируемы на 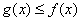 , то
, то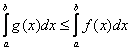
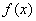 расположен не ниже графика функции
расположен не ниже графика функции  , поэтому площадь
, поэтому площадь  будет не меньше, а на практике почти всегда –больше площади
будет не меньше, а на практике почти всегда –больше площади  .
. и прямыми
и прямыми 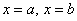 :
:
 на
на 

 непрерывна на отрезке
непрерывна на отрезке  , а значит, достигает на нём
, а значит, достигает на нём 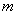 и
и  – наименьшего и наибольшего значений. Решаем стандартную двухшаговую задачу по нахождению
– наименьшего и наибольшего значений. Решаем стандартную двухшаговую задачу по нахождению  :
: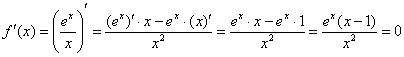
 – критическая точка.
– критическая точка.


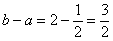


 и не больше площади зелёного прямоугольника
и не больше площади зелёного прямоугольника  :
:
 является неберущимся, и вычислить заштрихованную площадь можно лишь с определённой точностью, например, методом трапеций, по формуле Симпсона, с помощью разложения функции в ряд, др. способами.
является неберущимся, и вычислить заштрихованную площадь можно лишь с определённой точностью, например, методом трапеций, по формуле Симпсона, с помощью разложения функции в ряд, др. способами. – такая, что
– такая, что  . Геометрический смысл теоремы я уже использовал при выводе формулы Ньютона-Лейбница, единственное, там речь шла о кусочке криволинейной трапеции, здесь же – о всей фигуре. Грубо говоря, всегда существует прямоугольник со стороной
. Геометрический смысл теоремы я уже использовал при выводе формулы Ньютона-Лейбница, единственное, там речь шла о кусочке криволинейной трапеции, здесь же – о всей фигуре. Грубо говоря, всегда существует прямоугольник со стороной  (длина отрезка интегрирования), площадь которого равна площади
(длина отрезка интегрирования), площадь которого равна площади