 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Несобственные интегралы по неограниченному промежутку. Теоремы сравнения
Определение. Если существует конечный предел Говорят, что в этом случае Во многих случаях достаточно установить сходится или расходится данный интеграл и оценить его значение. Для этого применяют теоремы сравнения. Теорема1. Пусть сходятся или расходятся одновременно. Если сходятся, то справделиво равенство Доказательство. Следует из аддитивности определенного интеграла по промежутку. Теорема2.Если F – первообразная к функции f на отрезке Определение. Если интеграл Последний интеграл – абсолютно сходящийся.
Формула прямоугольников Дана непрерывная функция на отрезке [a,b]. Требуется вычислить определенный интеграл Составим суммы:
Каждая из этих сумм – интегральная сумма для f(x) на отрезке [a,b] и поэтому приближенно вычисляет интеграл.
Суть метода прямоугольников для отрезка [a,b] проиллюстрирована на рисунке, при этом площадь под кривой f(x) заменена суммой площадей заштрихованных прямоугольников. Примечание. Чем больше число шагов n, тем незначительнее ошибка при вычислении интеграла.
Формула трапеций. Эта формула является более точной по сравнению с формулой прямоугольников, что объясняется заменой ступенчатой линии на вписанную ломаную.
y1 у2 уn
a x1 x2 b x
Геометрически площадь криволинейной трапеции заменяется суммой площадей вписанных трапеций. Площади вписанных трапеций вычисляются по формулам:
После приведения подобных слагаемых получаем формулу трапеций: Число n выбирается произвольно. Чем больше оно будет, тем меньше будет шаг
Выбор числа шагов при заданной точности. Вычислить приближенное значение с заданной точностью означает, что выполняется неравенство: При вычислениях интеграла погрешность учитывается следующим образом:
Поиск по сайту: |
 то этот предел называют несобственным интегралом от функции на промежутке
то этот предел называют несобственным интегралом от функции на промежутке 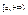 и обозначают так
и обозначают так 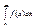
 интеграл существует/сходится. Если
интеграл существует/сходится. Если  при
при 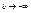 не имеет конечного предела, то говорят что он расходится/не существует.
не имеет конечного предела, то говорят что он расходится/не существует. тогда несобственные интегралы
тогда несобственные интегралы 

 то остается справедливой формула Ньютона-Лейбница в виде
то остается справедливой формула Ньютона-Лейбница в виде 
 сходится, то сходится и
сходится, то сходится и  Разделим отрезок на n равных частей длины
Разделим отрезок на n равных частей длины  точками
точками 
 Обозначим через
Обозначим через  значения f(x) в этих точках,т.е.
значения f(x) в этих точках,т.е. 


 или
или 




 тем с большей точностью вычисляется значение интеграла.
тем с большей точностью вычисляется значение интеграла.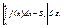
 - приближенное значение,
- приближенное значение,  - заданная погрешность.
- заданная погрешность.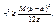 М – наибольшее значение модуля второй производной на заданном отрезке.
М – наибольшее значение модуля второй производной на заданном отрезке.