 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Свойство2. Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов от слагаемых
Доказательство. Свойство3.Если на отрезке[a,b],гдеа<b,функцииf(x) иj(х) удовлетворяют условию Доказательство.Рассмотрим разность
Каждая разность Сл-но, неотрицательно каждое слагаемое, неотрицательны вся сумма и весь предел. Свойство4.Если m и М – наименьшее и наибольшее значения функции f(x) на отрезке [a,b] и
Доказательство.По условию
Подставляя 2 последние выражения в неравенство получаем исходное неравенство. Свойство5 (теорема о среднем).Если функция f(x) непрерывна на отрезке [a,b], то на этом отрезке найдется такая точка Доказательство.Пусть a<b, m – наименьшее значение функции, М – наибольшее значение f(x) на отрезке [a,b]. Тогда получаем
Так как функция непрерывна на отрезке, то она принимает все промежуточные значения, заключенные между m и М. Следовательно, при некотором значении Примечание автора. Доказательство приведено и в одном из следующих вопросов. Свойство6.Для любых трех чисел a,b,c справедливо равенство Доказательство.Допустим сначала, что Так как предел интегральной суммы не зависит от способа разбиения отрезка, будем разбивать отрезок так, чтобы точка с была точкой деления. Тогда Переходя к пределу при Если Поэтому имеем Аналогично доказывается это свойство при любом взаимном расположении трех точек. Свойство определенного интеграла – теорема о среднем. Обобщенная теорема о среднем. Теорема.Если функция f(x) непрерывна на отрезке [a,b], то на этом отрезке найдется такая точка Доказательство.Пусть a<b, m – наименьшее значение функции, М – наибольшее значение f(x) на отрезке [a,b]. Тогда получаем
Так как функция непрерывна на отрезке, то она принимает все промежуточные значения, заключенные между m и М. Следовательно, при некотором значении Геометрический смысл теоремы. Величина определенного интеграла при f(x) ³ 0 равна площади прямоугольника, имеющего высоту f(c) и основание (b–a). Обобщенная теорема о среднем. Если функции f(x) и j(x) непрерывны на отрезке [a,b], и функция j(х) знакопостоянна на нем, то на этом отрезке существует точка e, такая, что
Поиск по сайту: |


 то
то 




 то
то




 что справедливо равенство:
что справедливо равенство: 
 Отсюда
Отсюда  где
где 
 будет
будет  то есть
то есть  если все эти три интеграла существуют.
если все эти три интеграла существуют. и составим интегральную сумму для функции f(x) на отрезке [a,b].
и составим интегральную сумму для функции f(x) на отрезке [a,b].
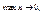 получим исходное соотношение.
получим исходное соотношение. на основании доказанного
на основании доказанного  или
или 

