|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теорема (признак Коши)
Теорема. Если в ряде с положительными членами 1. ряд сходится, при l<1, 2. ряд расходится при l>1. Доказательство. 1. Пусть l<1.Рассмотрим q, при котором Начиная с некоторого N ( Отсюда следует, что Рассмотрим 2 ряда:
Второй ряд сходится, так как его члены образуют убывающую геометрическую прогрессию. 2. Пусть l>1.С некоторого n=N будет иметь место неравенство Ряд расходится, так как его общий член не стремится к нулю (все члены больше 1). Замечание. Как и в признаке Даламбера случай
Теорема (признак Даламбера). Теорема. Если в ряде с положительными членами 1.ряд сходится, при l<1, 2. ряд расходится при l>1, 3. теорема не дает ответа при l=1. Доказательство. 1. Пусть l<1.Рассмотрим q, при котором Начиная с некоторого N ( Действительно, так как величина Начиная с любого N, получаем систему неравенств:
Складывая таким образом члены последовательности, приходим к выводу, что перед нами геометрическая прогрессия со знаменателем 2. Пусть l>1.Из равенства Замечание1. Ряд будет расходиться и том случае, когда Замечание2.Если
Интегральный признак сходимости. Теорема. Пусть члены ряда Доказательство. Примечание автора. Необходимы 2 графические иллюстрации. Из первого графика очевидно Из второго - Рассмотрим первый случай (сходится). Предположим, что интеграл сходится Рассмотрим второй случай (расходится). Предположим, что Замечание. Ни признак Даламбера, ни признак Коши не решают вопроса о сходимости этого ряда, так как предел равен единице.
Поиск по сайту: |
 величина
величина 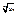 имеет предел
имеет предел  при
при 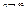 , т.е.
, т.е.  то:
то: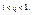
 ) выполняется неравенство
) выполняется неравенство 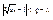
 или
или  для всех
для всех 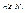

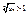 или
или 
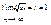 требует дополнительного исследования. Среди рядов, удовлетворяющих этому условию, могут встретиться как сходящиеся, так и расходящиеся ряды.
требует дополнительного исследования. Среди рядов, удовлетворяющих этому условию, могут встретиться как сходящиеся, так и расходящиеся ряды.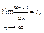 то:
то: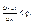
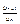 стремится к
стремится к 
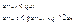

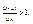
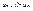 Это означает, что члены ряда возрастают, поэтому ряд расходится.
Это означает, что члены ряда возрастают, поэтому ряд расходится.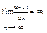 Это следует из неравенства
Это следует из неравенства  но отношение
но отношение 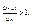 то
то 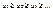 и пусть f(x)– такая непрерывная невозрастающая функция, что
и пусть f(x)– такая непрерывная невозрастающая функция, что 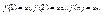 Тогда если несобственный интеграл
Тогда если несобственный интеграл  сходится/расходится, то сходится/расходится и ряд.
сходится/расходится, то сходится/расходится и ряд.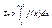
 откуда
откуда 
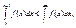
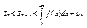 Частичная сумма
Частичная сумма  остается ограниченной при всех значениях n. Но при увеличении n она возрастает, так как все члены положительны. Следовательно, ряд сходится.
остается ограниченной при всех значениях n. Но при увеличении n она возрастает, так как все члены положительны. Следовательно, ряд сходится.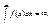 Это значит, что при возрастании n неограниченно возрастает интеграл
Это значит, что при возрастании n неограниченно возрастает интеграл 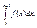 Тогда в силу
Тогда в силу